Схемы сравнения двоичных кодов

Многоразрядная схема сравнения служит для регистрации совпадения двух n-разрядных чисел:

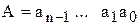и .

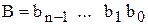Она строится из n одноразрядных схем, сравнивающих цифры 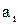и 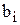этих чисел поразрядно.

На основе таблицы истинности одноразрядной системы сравнения (табл.1) определить СДНФ функции равнозначности 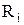и функции неравнозначности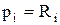

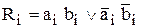(ИЛИ) (+) (3.1)

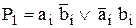. (3.2)

Для обнаружения совпадени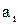й и 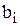во всех разрядах чисел А и В следует образовать конъюнкции всех n переменных, т.е.

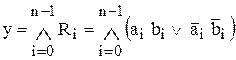
или

.

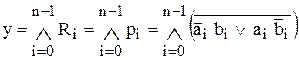Многоразрядная схема сравнения двух чисел А и В представляет собой логическую схему, реализующую ПФ вида (3) или (4). На рис. 1 приведена схема сравнения на ЛЭ типа И и ИЛИ для 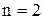по функции равнозначности и изображено условное обозначение схемы сравнения.

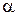
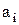
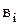
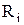
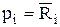
Более универсальными являются цифровые компараторы, которые, помимо регистрации равенства двух чисел, могут установить, какое из них больше. Обычно такие компараторы имеют три выхода 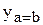, 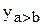и 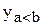. Простейшая задача состоит в сравнении двух одноразрядных чисел 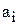и 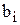. Такое сравнение реализуется следующими ПФ:

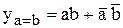
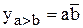
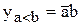
Аналогичные ПФ могут быть составлены для сравнения многоразрядных чисел. Однако при увеличении разрядности сложность этих ПФ быстро растёт и форма их представления теряет надёжность. Поэтому для сравнения многоразрядных чисел используют следующий алгоритм. Сначала сравнивают значения старших разрядов; если они различны, то эти разряды и определяют результаты сравнения; если же они равны, то необходимо сравнивать следующие за ними более младшие разряды и т.д. При этом многоразрядный компаратор может быть реализован в виде каскадного соединения более простых первичных компараторов, имеющих дополнительно входы 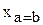, , 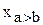, 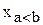соединяемые с одноимёнными выходами первичного компаратора предыдущего каскада (рис. 3.9.).

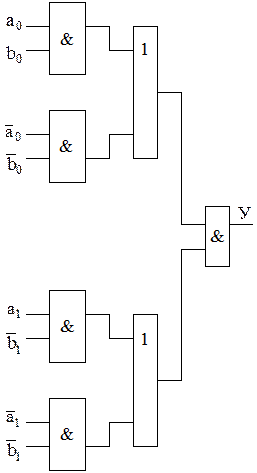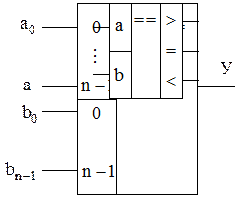Рис. 3.9.

Одноразрядный первичный компаратор описывается следующими ПФ:

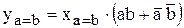
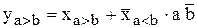
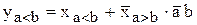
Первичные компараторы на четыре и более разрядов выпускаются в интегральном исполнении.