Корень натуральной степени из комплексного числа
Корнем степени n из комплексного числа z, где 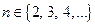 , называется комплексное число w, такое что
, называется комплексное число w, такое что 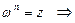
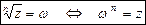 .
.
Например, 1) 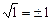 , так как
, так как 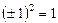 ;
;
2) 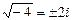 , так как
, так как 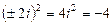 ;
;
3) 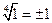 или
или 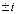 , так как
, так как 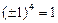 и
и 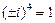 .
.
Из определения очевидно следует, что операция извлечения корня из комплексного числа является многозначной.
Если использовать формулу Муавра, то нетрудно доказать следующее утверждение.
| Теорема о значениях корня из комплексного числа |
Корень натуральной степени 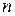 существует для любого комплексного числа существует для любого комплексного числа 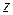 и если и если 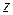 ¹ 0, то ¹ 0, то 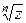 имеет имеет 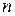 различных значений, вычисляемых по формуле различных значений, вычисляемых по формуле
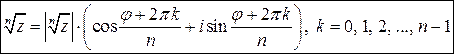 Извлечение корня натуральной степени из комплексного числа (8)
где Извлечение корня натуральной степени из комплексного числа (8)
где 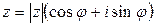 , , 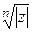 — значение арифметического корня на — значение арифметического корня на 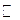 . .
|
Геометрически, все значения 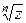 расположены регулярным образом на окружности радиусом
расположены регулярным образом на окружности радиусом 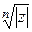 с начальным углом
с начальным углом 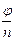 и углом регулярности
и углом регулярности 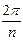 .
.
Примеры (вычисление корня из комплексных чисел)
 1)
1) 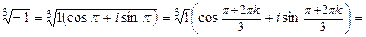
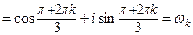 , k = 0, 1, 2 Þ
, k = 0, 1, 2 Þ
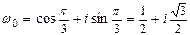 ,
,
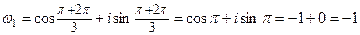 ,
,
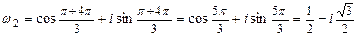 .
.
2) 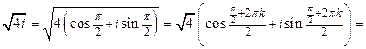
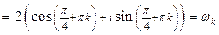 ,
, 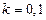
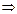
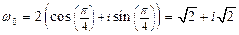 ,
, 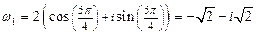 .
.
Нетрудно показать, что корень квадратный 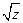 существует на множестве комплексных чисел для любых
существует на множестве комплексных чисел для любых 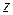 и имеет два противоположных значения при
и имеет два противоположных значения при  :
: 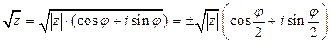 .
.
Дата добавления: 2021-07-22; просмотров: 564;











