Искажение входного тока выпрямителей и пульсации выпрямленного напряжения, выходные фильтры.

Как правило, любой преобразователь на базе АИН содержит входной и выходной фильтры. Требование применения входного фильтра обусловлено тем, что кривая входного тока инвертора напряжения, независимо от схемного варианта, имеет достаточно сложную форму, с разрывами в моменты коммутаций. Поскольку выходное сопротивление источника питания (например, выпрямителя) обычно имеет индуктивный характер (в лучшем случае это индуктивность токоподводящих шин), то, для предотвращения перенапряжений на входе инвертора и соответствующих искажений выходного напряжения, на входе инвертора необходим емкостный или Г-образный фильтр.

Применение Г-образного фильтра желательно для предотвращения попадания высокочастотных составляющих входного тока инвертора в источник питания, например, в сетевой выпрямитель, если преобразователь питается от сети промышленной частоты.

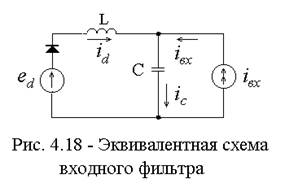
На эквивалентной схеме такого фильтра, показанной на рис. 4.18, источник эдс 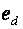отображает мгновенное значение выходного напряжения выпрямителя, источник тока - мгновенное значение входного тока инвертора. Параметры фильтра должны выбираться таким образом, чтобы обеспечить как сглаживание пульсаций выходного напряжения выпрямителя, так и предотвращение попадания высокочастотных составляющих входного тока инвертора в выпрямитель. Первая задача может быть решена стандартными методами [1,3], а вторая сводится к расчету амплитуды переменной составляющей напряжения на емкости фильтра, при допущении, что переменная составляющая входного тока инвертора полностью замыкается через емкость фильтра [4,5]. Это допущение справедливо при условии, что реактивное сопротивление индуктивности фильтра для самой низкочастотной гармоники входного тока в 5-10 раз больше соответствующего реактивного сопротивления емкости. При этом возникают две трудности: первая, это выбор допустимой величины амплитуды переменной составляющей на емкости фильтра, а вторая, это расчет спектра входного тока инвертора.

При выборе допустимой величины амплитуды переменной составляющей напряжения на емкости фильтра необходимо иметь в виду, что для электролитических конденсаторов эта величина ограничена изготовителем и составляет, как правило, не более 3-4 % от номинального рабочего напряжения (обычно на частоте 50 Гц). Для фильтровых конденсаторов зарубежных фирм иногда задается допустимая величина переменной составляющей тока (с частотой 100 Гц), которая может замыкаться через конденсатор.

Кроме того, если этих ограничений нет, (например, при использовании частотных конденсаторов) то следует учитывать, что увеличение пульсаций на емкости фильтра приводит к искажению кривой выходного напряжения инвертора.

Точный расчет спектрального состава кривой входного тока относительно простыми методами возможен только в случаях, когда не применяется широтно-импульсная модуляция. При использовании ШИМ задача резко усложняется, а аналитические результаты мало удобны для практического использования. С другой стороны, для выбора емкости фильтра достаточно иметь оценки амплитуд низкочастотных составляющих кривой входного тока, которые могут быть получены по приближенным соотношениям. Достаточно точные для практических расчетов результаты могут быть получены путем компьютерного моделирования. Например, на рис. 4.19 показаны результаты моделирования электромагнитных процессов в однофазной мостовой схеме АИН при однополярной модуляции в среде MicroCap-VI. Частота модулирующего сигнала равна 100 Гц, несущая частота – 2 кГц и коэффициент модуляции – 0,7. На рис. 4.19(а) хорошо видно, что кривая тока нагрузки имеет ощутимый сдвиг фазы. На рис. 4.19(б) показана кривая входного тока инвертора. Характерно, что огибающая кривой входного тока имеет такой же вид, как и кривая входного тока инвертора, работающего без широтно-импульсной модуляции (см. рис. 1.2(б)). В спектре входного тока, показанном на рис. 4.19(в), хорошо видны постоянная составляющая и первая гармоника огибающей кривой входного тока, имеющая частоту равную двойной частоте модулирующего сигнала. Присутствуют также гармоники, частоты которых кратны или несущей частоте, или комбинационным частотам, т.е. частотам кратным сумме или разности несущей частоты и частоты модуляции.

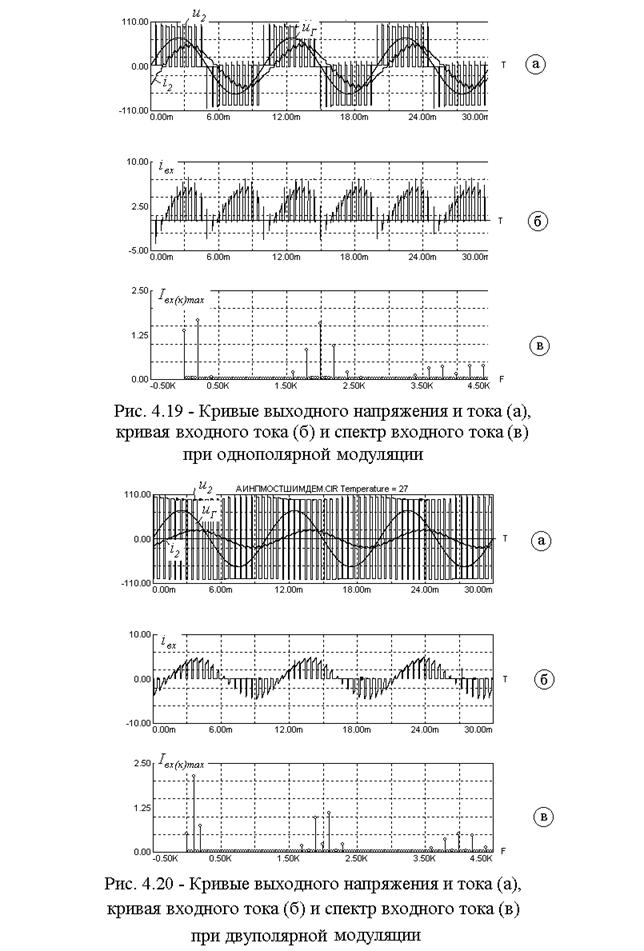
Аналогичные кривые показаны на рис. 4.20 для полумостовой

схемы инвертора, работающей с двуполярной модуляцией при тех же частотах, что и в предыдущем случае. Однако в этом случае кривая входного тока имеет иной вид, и в спектре, соответственно, в два раза меньше величина постоянной составляющей, а частота первой гармоники пульсаций равна частоте модулирующего сигнала.

Для расчета емкости фильтра основное значение имеют амплитуда и частота первой гармоники пульсаций входного тока. Соответствующие расчетные соотношения для разных схем инверторов (и при разных законах управления ими) были приведены в предыдущих разделах. В большинстве случаев, частота первой гармоники пульсаций входного тока определяется соотношением:

, (4.70)

а, соответственно, её амплитуда может быть рассчитана по (4.56):

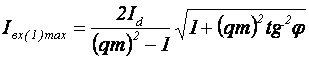. (4.71)

где - произведение, известное в теории выпрямления под названием пульсности схемы [1]. В этом произведении 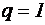для схем с выводом нулевой точки (в нашем случае, однотактных), и 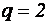для мостовых схем; - число фаз преобразователя. В частности, для однофазной полумостовой схемы инвертора , а для трех фазной мостовой без нулевого провода ;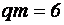

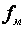- частота модулирующего напряжения;

- среднее значение входного тока.

Таким образом, если задана допустимая величина амплитуды первой гармоники переменной составляющей на емкости , то должно выполняться условие:

. (4.72)

Отсюда, полагая и , будем иметь:

. (4.73)

Зная величину емкости можно определить индуктивность

фильтра, исходя из условия :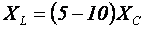

. (4.74)

При окончательном выборе параметров фильтра необходимо убедиться в том, что резонансная частота фильтра не равна и не кратна частоте пульсаций выпрямленного напряжения.

Одной из проблем, возникающих при применении Г-образного фильтра в звене постоянного тока, является возникновение перенапряжений на элементах фильтра при изменении тока нагрузки и, в частности, при включении выпрямителя. Достаточно опасным является включение выпрямителя при отсутствии управляющих импульсов на силовых ключах инвертора или при отсутствии нагрузки на выходе инвертора. В этом случае перенапряжение на емкости может превышать нормальное напряжение почти в два раза. Соответственно, при отключении тока нагрузки, например, при срабатывании токовой защиты, величина перенапряжения на емкости фильтра может составить величину, определяемую соотношением:

, (4.75)

где - добротность контура, содержащего . Обычно это величина порядка 10-15;

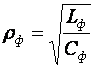- волновое сопротивление контура;

- величина тока в реакторе в момент срабатывания защиты.

Нетрудно видеть, что в переходных процессах перенапряжения, возникающие на емкости фильтра, могут быть опасны, как для элементов фильтра, так и для силовых приборов инвертора. Поэтому желательно применение соответствующих мер для ограничения этих перенапряжений, например, схемы "мягкого" пуска [14] или включение варисторов параллельно фильтровому конденсатору.

Фильтр на выходе инвертора в большинстве случаев также весьма желателен. Например, даже при использовании инвертора с ШИМ в системе частотно-регулируемого электропривода наличие в токе статора ощутимых составляющих несущей частоты приводит к увеличению потерь в двигателе, а наличие высокочастотного напряжения на зажимах статора вызывает ускоренное старение изоляции. Если же инвертор используется как источник вторичного электропитания, например, на борту подвижного объекта, то выполнение стандартных требований, предъявляемых к качеству выходного напряжения, без выходных фильтров просто невозможно.

Возможные схемы выходных фильтров и рекомендации по выбору их параметров можно найти в литературе [4,5,15]. Чаще всего применяется Г-образный фильтр, эквивалентная схема которого показана на рис. 4.21(а). Как известно [11], модуль комплексного коэффициента передачи такого фильтра описывается уравнением:

, (4.76)

где 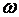- круговая частота сигнала;

- резонансная частота фильтра;

- волновое сопротивление фильтра;

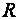- сопротивление нагрузки.

Уравнение (4.76) показывает, что коэффициент передачи фильтра, особенно на частотах близких к резонансной частоте, существенно зависит от соотношения между параметрами фильтра и сопротивлением нагрузки. На рис. 4.21(б) показаны амплитудно-частотные характеристики Г-образного фильтра, построенные для разных отношений . Как видно из этих характеристик, для того чтобы напряжение на выходе фильтра мало зависело от изменения нагрузки необходимо, чтобы рабочая частота была или существенно меньше резонансной или хотя бы раза в 2-3 больше. С другой стороны, используя определения волнового сопротивления и резонансной частоты, нетрудно показать, что параметры фильтра однозначно определены величинами и :

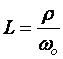(4.77)

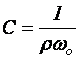. (4.78)

Приведенные соотношения показывают, что величины элемен-

тов фильтра и, следовательно, их масса и габариты обратно пропорциональны резонансной частоте фильтра. Таким образом, с точки зрения снижения массы фильтра, первая гармоника выходного напряжения инвертора, которая должна передаваться фильтром без заметного ослабления, должна иметь частоту ниже резонансной частоты фильтра. Причем, как видно на рис. 4.21(б), если частота выходного напряжения ниже резонансной частоты фильтра на порядок, то коэффициент передачи фильтра равен единице при любых параметрах нагрузки.

Такое соотношение легко реализовать в инверторах с ШИМ по синусоидальному закону, в которых гладкая составляющая выходного напряжения имеет, практически синусоидальную форму и, следовательно, не содержит низкочастотных гармоник. При этом ближние высокочастотные гармоники имеют частоту близкую к несущей, и обычно отличаются от частоты модулирующего сигнала в десятки раз. Здесь, однако, следует отметить, что при изменении кратности несущей частоты по отношению к частоте модулирующего напряжения (например, при регулировании частоты выходного напряжения), в выходном напряжении инвертора возможно появление субгармонических составляющих, которые Г-образным фильтром подавить невозможно.

Выходное напряжение инвертора без ШИМ может содержать достаточно близкие низкочастотные гармоники. В этом случае, резонансная частота фильтра должна находиться между частотой первой гармоники и частотой ближней высшей гармоники выходного напряжения. На рис. 4.22(а) представлены зависимости модуля

комплексного коэффициента передачи фильтра от соотношения между частотой первой гармоники выходного напряжения 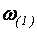и резонансной частотой фильтра . Верхняя кривая рассчитана по уравнению (4.76) для условия 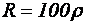, что соответствует изменению напряжения холостого хода (в о.е.) при изменении соотношения частот. Соответственно, нижняя кривая рассчитана для условия 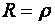, и дает зависимость выходного напряжения при номинальной нагрузке. На рис. 4.22(б) показана зависимость приращения коэффициента передачи от соотношения частот, которое пропорционально наклону внешней характеристики преобразователя, определяемому параметрами фильтра. Приведенные кривые показывают, по мере приближения к резонансной частоте наблюдается рост напряжения холостого хода и увеличивается наклон внешней характеристики инвертора.

Нетрудно убедиться, что для инвертора, имеющего прямоугольную форму выходного напряжения, резонансную частоту фильтра придется выбрать ниже частоты первой гармоники, в противном случае ближняя, третья гармоника фильтром подавляться не будет. Можно показать, что в этом случае с помощью обычного Г-образного фильтра получить коэффициент гармоник порядка 0,1, как требует действующий стандарт, невозможно. Действительно, если частота первой гармоники выбрана в 2-3 раза выше резонансной частоты фильтра, то коэффициент передачи фильтра для высших гармоник, приблизительно, обратно пропорционален квадрату номера гармоники. Поскольку амплитуды высших гармоник выходного напряжения инвертора тоже убывают пропорционально номеру гармоники, то спектр напряжения на выходе фильтра имеет вид:

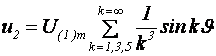. (4.79)

Тогда, коэффициент гармоник можно найти по определению:

. (4.80)

Сумма под корнем является стандартным рядом, который сходится к величине 1,0518. Соответственно, коэффициент гармоник, вычисленный по (4.80) равен 0,227, что более чем в два раза превышает допустимую величину. Расчеты показывают, что даже в трехфазном варианте, когда кривая выходного напряжения не содержит третьей и кратных трем гармоник, на выходе фильтра коэффициент гармоник равен 0,113.

Задача получения выходного напряжения требуемого качества может быть успешно решена при использовании ШИМ того или иного типа. Выбор параметров фильтра в этом случае можно сделать, если предположить, что ближние высшие гармоники имеют частоту равную несущей. Амплитуда первой гармоники несущей частоты при двуполярной модуляции максимальна при коэффициенте модуляции равном нулю и равна:

. (4.81)

Соответственно, амплитуда высокочастотной составляющей на выходе фильтра определяется соотношением:

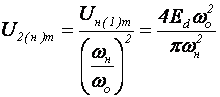. (4.82)

Отсюда, задавшись допустимой величиной амплитуды высокочастотной составляющей на выходе, можно определить резонансную частоту фильтра:

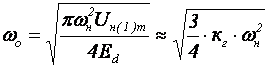. (4.83)

Если задаться величиной волнового сопротивления фильтра , то по (4.77) и (4.78) нетрудно определить параметры элементов фильтра.

Аналогично можно рассчитать параметры фильтра и при однополярной модуляции, сделав допущение, что амплитуда первой гармоники несущей частоты в этом случае, приблизительно в два раза меньше, чем при двуполярной модуляции.