Трехфазный инвертор напряжения, способы управления и характеристики.

Трехфазный АИН с нулевым проводом

Одним из простейших вариантов схем трехфазных АИН является инвертор, состоящий из трех однофазных полумостовых инверторов (аналогичных рассмотренному в предыдущем разделе), управляемых со сдвигом на 120 градусов. Схема инвертора показана на рисунке 2.1, а развертки импульсов управления транзисторами – на рисунке 2.2. На рисунке 2.3 показаны развертки выходных напряжений и токов в фазах А и В, и линейного напряжения между этими фазами при активно-индуктивной нагрузке. Кривые построены в предположении, что положительная полуволна выходного напряжения каждой фазы формируется при включении транзистора, имеющего четный номер. Номера транзисторов соответствуют очередности выработки управляющих импульсов. Например, положительная полуволна напряжения фазы А формируется при включении транзистора VT4 в момент времени 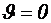. Соответственно, отрицательная полуволна формируется при включении транзистора VT1 при 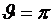Амплитуда фазного напряжения равна напряжению на верхней емкости фильтра C_Ф1, которое составляет половину напряжения источника питания E_d. Ток нагрузки фазы А замыкается через нулевой провод. При наличии нулевого провода, соединяющего нулевую точку звезды нагрузки со средней точкой входного фильтра, каждая фаза инвертора работает независимо друг от друга. В принципе, возможно два способа управления транзисторами инвертора: с длительностью управляющих импульсов 180 градусов, и с длительностью управляющих импульсов 120 градусов. Поскольку при втором способе управления форма выходного напряжения зависит от параметров нагрузки [3,5], то в настоящее время, как правило, используется лишь первый способ. При длительности управляющих импульсов равной 180 градусов кривая фазного напряжения имеет прямоугольную форму с амплитудой равной половине напряжения в звене постоянного тока. Соответственно, спектр выходного напряжения одной фазы содержит все нечетные гармоники, а действующее значение первой гармоники выходного напряжения определяется соотношением (1.18):

(2.1)

Кривая линейного напряжения показана на рисунке 2.3.

Амплитуда линейного напряжения равна напряжению E_d, а длительность импульса – 120 градусов. Равенство нулю линейного напряжения соответствует тем моментам, когда фазные напряжения равны. Например, на интервале одновременно включены транзисторы VT4 и VT6, следовательно, потенциалы фаз А и В равны потенциалу верхней шины моста, а, соответственно, их разность потенциалов равна нулю.

Исходя из кривой линейного напряжения, нетрудно определить его действующее значение:

(2.2)

При вычитании напряжений фаз А и В, первые гармоники которых сдвинуты на 120 градусов, происходит компенсация третьей гармоники и высших гармоник с номерами кратными трем. Соответственно, действующее значение первой гармоники линейного напряжения больше фазного в раз:

(2.3)

Форма кривой входного тока инвертора зависит от характера нагрузки. На рисунке 2.4 показаны развертки тока фазы А, входного тока 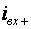(потребляемого положительной шиной моста), и тока нулевого провода при чисто активной нагрузке. Очевидно, что в этом случае ток фазы равен:

(2.4)

В течение периода выходного напряжения происходит шесть переключений силовых транзисторов и, соответственно, имеется шесть состояний схемы, которые чередуются через 60 градусов. Соответствующие интервалы пронумерованы на рисунке 2.4 а. В соответствии с алгоритмом формирования управляющих импульсов, показанном на рисунке 2.2, на первом интервале включены транзисторы VT2, VT3 и VT4. То есть, включены два транзистора верхней группы (имеющих общие коллекторы) и лишь один транзистор нижней группы (имеющих общие эмиттеры). Следовательно, к верхней шине моста подключены две фазы нагрузки, а к нижней только одна. Таким образом, от верхней полови-

ны входного фильтра потребляется ток 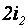, а от нижней - 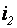. Разность этих токов замыкается через нулевой провод.

Через 60 градусов выключается транзистор VT2 и включается транзистор VT5, теперь две фазы нагрузки подключены к нижней шине моста и лишь одна к верхней. Соответственно, ток верхней половины фильтра уменьшается в два раза, а ток нижней – увеличивается. Разность этих токов опять же замыкается через нулевой провод. Аналогичное изменение структуры схемы происходит при каждом переключении силовых транзисторов – шесть раз за период выходного напряжения.

Таким образом, через нулевой провод течет ток с амплитудой равной амплитуде тока фазы, но с тройной частотой. Такую же частоту имеет первая гармоника пульсаций входного тока.

Среднее значение входного тока при активной нагрузке определяется очевидным соотношением:

(2.5)

Таким образом, амплитуда переменной составляющей входного тока равна половине амплитуды тока нагрузки и, соответственно, амплитуда первой гармоники пульсаций входного тока:

, (2.6)

причем частота первой гармоники пульсаций входного тока равна утроенной частоте выходного напряжения.

На рисунке 2.5 показаны кривые токов в схеме при активно-индуктивном характере нагрузки. Поскольку в этом случае кривая тока нагрузки состоит из отрезков экспоненты, соответственно изменился вид кривых входного тока и тока нулевого провода. В то же время, нетрудно видеть, что мгновенные значения входного тока на четных и нечетных интервалах отличаются, что приводит к появлению в этой кривой составляющей тройной частоты.

Спектральный состав входного тока инвертора можно определить, если просуммировать спектры входных токов каждой фазной ячейки, поскольку, в соответствии с первым законом Кирхгофа, можно записать:

(2.7)

Спектр входного тока фазной ячейки можно рассчитать методом коммутационных функций. Действительно, полагая, что кривая выходного напряжения имеет прямоугольную форму, можно представить напряжение фазы А как результат умножения эдс источника питания на коммутационную функцию:

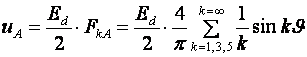(2.8)

где 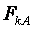определена по (1.2) и (1.3).

В этом случае, комплексное сопротивление нагрузки для 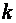-той гармоники равно:

(2.9)

Следовательно, спектр тока нагрузки фазы А описывается следующим тригонометрическим рядом:

(2.10)

где ; (2.11)

(2.12)

Величины 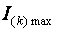и , используемые в уравнении (2.10) – амплитуда и фаза 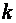-той гармоники тока нагрузки, соответственно.

Как следует из принципа действия полумостовой схемы АИН, ток верхней половины схемы существует только на интервале от нуля до 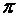(см. рисунок 1.4д). Следовательно, для расчета кривой входного тока фазной ячейки можно использовать коммутационную функцию следующего вида:

. (2.13)

Подставив (1.1) в (2.13) легко убедиться, что:

(2.14)

Тогда, используя (2.13) можно записать:

(2.15)

После подстановки (2.10) и (1.3) в (2.15) получим:

(2.16)

Индексы членов ряда коммутационной функции в (2.16) заменены на , поскольку перемножение рядов должно выполняться почленно. После раскрытия скобок в выражении для 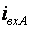можно выделить две составляющих, одна из которых содержит нечетные гармоники, кратные частоте выходного напряжения, образующиеся после перемножения ряда для выходного тока на 1/2, а вторая составляющая содержит четные гармоники, образующиеся после перемножения рядов.

Первая составляющая равна:

(2.17)

Как известно [6]:

(2.18)

Поэтому вторая составляющая представляет собой бесконечную матрицу, содержащую косинусные гармоники суммарных и разностных частот. Результаты перемножения первых трех членов каждого ряда показаны в таблице 2.1.

Таблица 2.1 – Матрица результатов перемножения первых трех членов рядов.

i\k
	;	;	;
	;	;	;
	;	;	;

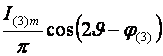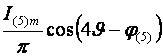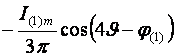
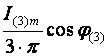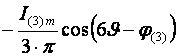
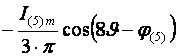
Верхние строки каждой ячейки матрицы соответствуют разностным частотам, а нижние – суммарным.

В частности, разностные частоты для 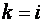равны нулю, а соответствующие коэффициенты, размещенные на главной диагонали матрицы, формируют постоянную составляющую входного тока. Выборка коэффициентов для составляющей "нулевой частоты" позволяет записать соотношение для постоянной составляющей входного тока в виде следующего ряда:

. (2.19)

Аналогично можно получить ряд для старшей гармоники пульсаций входного тока, имеющей двойную частоту. Эта гармоника формируется при суммировании частот первых членов ряда ( ) и вычитании частот следующих членов ( ).

Подставив (2.11) в (2.19) и выразив косинус через тангенс, будем иметь:

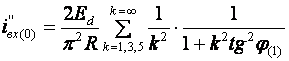; (2.20)

Интересно отметить, что при чисто активной нагрузке ( ), когда второй сомножитель под знаком суммы равен единице, оставшаяся часть ряда сходится к величине . Тогда уравнение (2.20) дает величину среднего значения входного тока полумостовой схемы АИН при чисто активной нагрузке:

(2.21)

Анализ остальных коэффициентов бесконечной матрицы показывает, что суммы коэффициентов при косинусах одинаковых частот при активной нагрузке строго равны нулю, а при активно-индуктивной нагрузке ими можно пренебречь.

Таким образом, полное выражение для кривой входного тока одной фазы можно представить в виде суммы постоянной составляющей по (2.20) и переменной составляющей по (2.17). Очевидно, что гармонический состав входных токов двух других фаз отличается от полученного выше только соответствующим сдвигом фазы. Следовательно, при суммировании входных токов трех однофазных полумостовых ячеек, будут складываться постоянные составляющие и составляющие гармоник тройной частоты. Что же касается первой гармоники входного тока и гармоник не кратных трем, то при симметричной нагрузке они образуют трехфазную систему токов, сумма которых равна нулю.

Все сказанное справедливо при условии равенства фазных токов. Если же нагрузки по фазам не равны, то результирующий спектр входного тока искажается. В частности, в этом случае в кривой входного тока появляется составляющая, имеющая частоту выходного напряжения.

Таким образом, среднее значение входного тока (при симметричной нагрузке) определяется уравнением:

(2.22)

Соответственно, спектральный состав переменной составляющей этого тока будет:

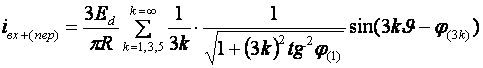. (2.23)

Анализ полученных соотношений показывает, что коэффициенты, находящиеся под знаком суммы, быстро убывают с ростом 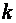. Поэтому для практических расчетов можно использовать лишь первые члены ряда, что существенно упрощает вид уравнений. Полагая и суммируя (2.22) и (2.23) получим приближенное выражение для входного тока трехфазного АИН:

(2.24)

где

Нетрудно убедиться, что соотношение для амплитуды первой гармоники пульсаций входного тока по (2.24) при (т. е. при чисто активной нагрузке), совпадает с (2.6), полученным из общих соображений.

Уравнение для тока в нулевом проводе можно получить, если сложить переменные составляющие входного тока положительной и отрицательной шин транзисторного моста. Действительно, емкости входного фильтра не пропускают постоянные составляющие входных токов, которые замыкаются через источник питания. С другой стороны, величины конденсаторов фильтра должны быть достаточно велики и, следовательно, переменные составляющие входных токов замыкаются через емкости фильтра. Спектры входных токов верхней и нижней шин моста одинаковы, но первая гармоника переменной составляющей входного тока нижней шины сдвинута по фазе по

отношению к первой гармонике переменной составляющей входного тока верхней шины на 180 эл. градусов. Таким образом, получим:

(2.25)

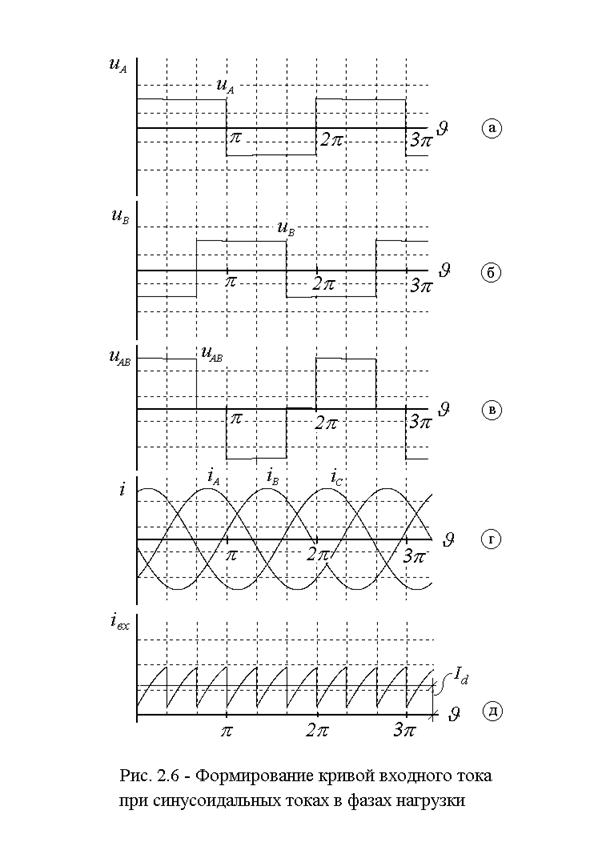
Довольно часто при расчете спектра входного тока АИН делается допущение о синусоидальности кривой тока в нагрузке. Формирование кривых входных токов трехфазного АИН, состоящего из трех полумостовых инверторов с нулевым проводом показано на рисунке 2.6. Расчет спектра входного тока можно выполнить таким же образом, как и при активно-индуктивной нагрузке, если в (2.10) положить , то есть всеми высшими гармониками тока нагрузки пренебречь.

Тогда уравнение для входного тока одной фазной ячейки можно записать в следующем виде:

, (2.26)

где ;

- натуральный ряд чисел.

При суммировании входных токов трех фазных ячеек (с учетом фазового сдвига) постоянные составляющие складываются, а в переменной составляющей сохраняются лишь гармоники с номерами кратными трем. Тогда, среднее значение входного тока АИН равно:

. (2.27)

Соответственно, амплитуда первой гармоники пульсаций входного тока, имеющая 6-ти кратную частоту ( ), определяется следующим уравнением:

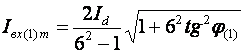(2.28)

Нетрудно видеть, что при симметричной нагрузке ток нулевого провода равен нулю, (в соответствии с исходным допущением о синусоидальности фазных токов) поскольку кривые входного тока на четных и нечетных интервалах одинаковы.

Таким образом, допущение о синусоидальности фазных токов приводит к качественным изменениям спектрального состава входного тока инвертора: исчезает гармоника тройной частоты в переменной составляющей. Кроме того, исчезает ток в нулевом проводе. Принимая во внимание, что при активно-индуктивной нагрузке трехфазного АИН, в реальной схеме ток в нулевом проводе существует при любых соотношениях параметров нагрузки, можно сделать вывод о том, что допущение о синусоидальности тока в нагрузке является слишком грубым и приводит к качественным погрешностям в результатах анализа.