Пример решения задачи
Оптимизировать сетевой график, изображенный на рис. 7, на котором указаны максимально возможные продолжительности работ (в сутках). Необходимые для оптимизации исходные данные представлены в таблице.
Таблица 8
| № п/п | работа (i,j) | продолжительность работы, сутки | коэффициент затрат на ускорение работы h(i,j) | стоимость работы, усл. руб. с=(i,j) при t(i,j)= b (i,j) | |
| минимальная а(i,j) | максимальная b (i,j) | ||||
| (0,1) | |||||
| (0,2) | |||||
| (1,2) | |||||
| (1,3) | |||||
| (2,7) | |||||
| (3,4) | |||||
| (3,5) | |||||
| (4,6) | |||||
| (5,6) | |||||
| (6,7) | |||||
| (7,8) | |||||
| итого |
Решение. Исходный для оптимизации план (рис.7) имеет максимальную продолжительность работ 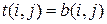 и соответственно минимальную стоимость с=300 (усл. руб.). Найдем все полные пути сетевого графика.
и соответственно минимальную стоимость с=300 (усл. руб.). Найдем все полные пути сетевого графика.
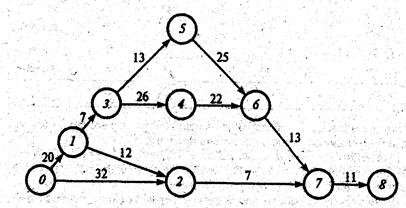
Рис. 7
их четыре:
l1 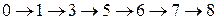 продолжительностью t(l1)=89 (суток);
продолжительностью t(l1)=89 (суток);
l2  продолжительностъю tкр= t(l2)=99 (суток);
продолжительностъю tкр= t(l2)=99 (суток);
l3 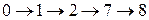 продолжительностью t(l3)=50(сугок);
продолжительностью t(l3)=50(сугок);
l4 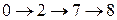 продолжительностью t(l4)=50 (сугок).
продолжительностью t(l4)=50 (сугок).
Для удобства дальнейших расчетов представим эти пути графически в виде цепочек работ (рис. 8), в которых цифры над стрелками показывают коэффициенты затрат на ускорение работ 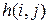 , а под стрелками - максимально возможные величины уменьшения продолжительности работ
, а под стрелками - максимально возможные величины уменьшения продолжительности работ 

Рис. 8.
i шаг. Уменьшить продолжительность выполнения комплекса можно, как известно, только за счет сокращения продолжительности работ критического пути tкр=t(l2). Из работ критического пути l2 наименьший коэффициент затрат на ускорение h(i,j) имеет работа (3,4): hmin(i,j)= min{h (0, 1); h (1, .3); h (3, 4); h (4, б); h (б, 7); h (7, 8)}= min{6; 8; 2; 4; 5; 9}=2, т.е. hmin(i,j)= h (3, 4)=2. продолжительность работы t(3,4) можно сокращать не более чем на 10 суток. при этом изменится длина только критического пути (с 99 до 89 суток) - l2 единственного из четырех путей, проходящего через работу (3,4), а стоимость проекта за счет ускорения работы (3,4) возрастет до 320 (усл. руб.). итак, на 1 шаге:
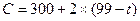 , где 89≤t≤99;
, где 89≤t≤99;
новые длины путей равны 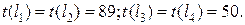
ii шаг. Теперь мы имеем два критических пути l1 и l2 и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности. Сократить одновременно t(l1) и t(l2) можно, уменьшив продолжительность работ, лежащих на этих путях: либо t(0, 1), либо t(6,7), либо t(7, 6). останавливаемся на t(6, 7), поскольку при этом обеспечивается минимум затрат на ускорение работы:
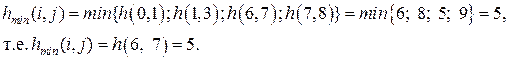
Продолжительность работы t(6,7), можно уменьшить не более на 5 суток. На эту величину уменьшатся длины критических путей t(l1) и t(l2), а следовательно, и срок выполнения проекта 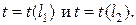 При этом стоимость проекта увеличится с 320 до 345 (усл. руб.). итак, на ii шаге:
При этом стоимость проекта увеличится с 320 до 345 (усл. руб.). итак, на ii шаге:
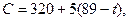 где 84≤t≤89;
где 84≤t≤89;
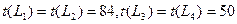
Продолжая аналогичным образом сокращать продолжительность работ, получим
iii шаг.
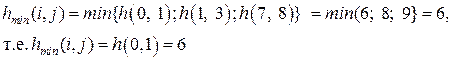
Сокращая продолжительностъ работы t(0, 1) до 10 суток, найдем
 где 74≤t≤84
где 74≤t≤84

iv шаг.
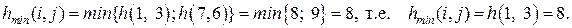 Сокращая продолжительность работы t(1, 3) до 5 суток, найдем
Сокращая продолжительность работы t(1, 3) до 5 суток, найдем
 где 69≤t≤74
где 69≤t≤74
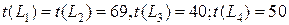
v шаг. сокращая продолжительность работы t(7, 8) до 5 суток, найдем (учитывая, что h (7, 8)=9)
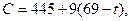 где 64≤t≤69
где 64≤t≤69

vi шаг. Теперь несокращенными остались продолжительности трех критических работ: t(3, 5) и t(5, 6) критического пути l1, каждую из которых можно сократить до 5 суток, и t(4, 6) критического пути l2, которую можно сократить до 10 суток. Сокращение какой-либо одной из названных величин не приведет к сокращению продолжительности выполнения проекта, ибо при этом сократится лишь один из двух путей, а длина несокращенного пути, который станет единственным критическим путем, не изменится. Поэтому, последовательно сокращая t(4, 6) и t(5, 6) до 5 суток (с учетом времени сокращения продолжительности работ), найдем (теперь коэффициент затрат на ускорение работ равен
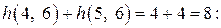
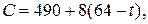 где 59≤t≤64;
где 59≤t≤64;
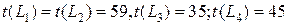
vii шаг. Продолжительность работы t(4, 6) можно сократить еще до 5 суток и на тот же срок можно сократить t (3, 5) (иначе срок выполнения проекта не изменится). Полагая, что 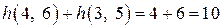 , найдем
, найдем
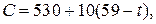 где 54≤t≤59
где 54≤t≤59
График оптимальной зависимости стоимости проекта с(t) от продолжительности его выполнения показан на рис. 9 с помощью этого графика можно, с одной стороны, оценить минимальную стоимость проекта при любом возможном сроке его выполнения, а с другой стороны - найти предельную продолжительность выполнения проекта при заданной его стоимости. Например, при продолжительности проекта t=79 (суток) минимальная стоимость выполнения рассматриваемого комплекса составит 375 (усл. руб.), а при стоимости выполнения комплекса, например, 540 (усл. руб.) предельная продолжительность проекта составит 55 (суток). С помощью функции с(t) можно оценить дополнительные затраты, связанные с сокращением сроков завершения комплекса. так, сокращение продолжительности проекта с 79 до 55 суток потребует дополнительных затрат 540-375=165 (усл. руб.).
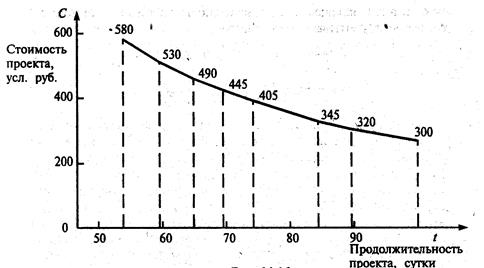
Рис. 9
Дата добавления: 2021-07-22; просмотров: 500;











