МЕТОД ГОМОРИ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
Метод Гомори является универсальным методом решения задач целочисленного программирования, с помощью которого после конечного числа итераций можно найти оптимальный план или убедиться в том, что задача не имеет решений. Однако практическая ценность метода Гомори весьма ограничена, так как при решении задач нужно выполнить довольно много итераций.
При решении задач целочисленного программирования методом Гомори из множества оптимальных планов задачи линейного программирования постепенно удаляются подмножества, которые не содержат целочисленных планов.
На первой итерации симплекс-методом нужно решить задачу линейного программирования. Если найденные неизвестные удовлетворяют требованию целочисленности, то задача целочисленного программирования решена. Если же среди найденных неизвестных хотя бы одна является дробным числом, то тогда следует составить дополнительное условие (как его составлять - об этом чуть ниже) и присоединить его к системе ограничений задачи целочисленного программирования. Таким образом, из множества планов удаляется подмножество, не содержащее целочисленных планов. Если оптимальный план дополненной таким образом задачи является целочисленным, то задача целочисленного программирования решена. Процесс решения продолжается то тех пор, пока на какой-либо итерации не будет найден целочисленный оптимальный план или можно убедиться, что задача не имеет решения.
Теперь о том, как составлять упомянутое дополнительное условие. Оно, дополнительное условие, получается из одного из уравнений системы ограничений из коэффициентов при неизвестных и самих неизвестных по формуле
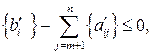
где в фигурных скобках - дробные части соответственно свободного члена и коэффициентов при неизвестных.
Например, из симплексной таблицы получаем такое уравнение:
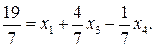
Дробную часть свободного члена получаем, вычитая из самого числа его целую часть следующим образом:
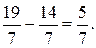
Аналогично получаем дробные части коэффициентов при неизвестных:
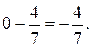 (при x3),
(при x3),
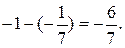 (при x4).
(при x4).
А общее правило нахождения дробных частей таково: целой частью вещественного числа a называется самое большое целое число [a], непревышающее a; дробной частью вещественного числа a называется разность {a} = a - [a] самого числа a и его целой части [a].
Далее следует преобразовать полученное неравенство в уравнение путём введения дополнительной неизвестной 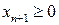 :
:
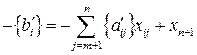 .
.
В нашем примере по приведённой выше формуле получается следующее уравнение:
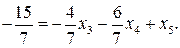
Пример. Решить методом Гомори следующую задачу целочисленного программирования. Найти максимум целевой функции
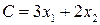
при системе ограничений
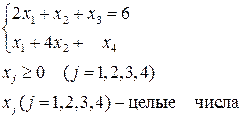
Решение. Решаем задачу симплекс-методом (сам метод объясняться здесь не будет, а будут приведены лишь симплексные таблицы.).
Дополнительные неизвестные x3 и x4 примем за базисные. Выразим базисные неизвестные и функцию цели через неосновные переменные:
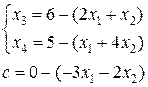
Из коэффициентов составим симплексную таблицу:
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | ||||
| X4 | ||||
| С | -3 | -2 |
Составляем следующие таблицы до получения оптимального плана:
| Таблица 2 | |||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | ||
| X3 | X2 | ||||
| X1 | 1/2 | 1/2 | |||
| X4 | -1/2 | 7/2 | -1 | ||
| С | 3/2 | -1/2 | |||
| Таблица 3 | |||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | ||
| X3 | X4 | ||||
| X1 | 19/7 | 4/7 | -1/7 | -1/2 | |
| X2 | 4/7 | -1/7 | 2/7 | ||
| С | 65/7 | 10/7 | 1/7 | 1/2 | |
Из таблицы 3 находим оптимальный план 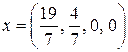 . Поскольку этот оптимальный план не удовлетворяет условию целочисленности, нам нужно составить дополнительное условие. Дробной частью координаты
. Поскольку этот оптимальный план не удовлетворяет условию целочисленности, нам нужно составить дополнительное условие. Дробной частью координаты 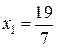 является число
является число 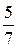 , а дробной частью координаты
, а дробной частью координаты 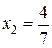 - число
- число 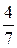 . Первое уравнение на основании таблицы запишется так:
. Первое уравнение на основании таблицы запишется так:
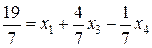
Определив дробные части коэффициентов при неизвестных и свободных членов, получаем следующее дополнительное условие:
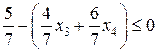
или, введя добавочную переменную 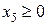 ,
,
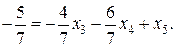
Получаем новую строку в симплексной таблице, полученной из таблицы 3 и добавления коэффициентов из только что полученного уравнения:
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 19/7 | 4/7 | -1/7 | -1/2 |
| X2 | 4/7 | -1/7 | 2/7 | |
| X5 | -5/7 | -4/7 | -6/7 | |
| С | 65/7 | 10/7 | 1/7 | 1/2 |
Совершаем шаг симплекс-метода и получаем таблицу:
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 17/6 | 2/3 | -1/6 | 1/7 |
| X2 | 1/3 | -1/3 | 1/3 | -2/7 |
| X4 | 5/6 | 2/3 | -7/6 | |
| С | 55/6 | 4/3 | 1/6 | -1/7 |
Получили оптимальный план 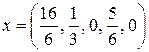 . Этот план, как и предыдущий, не удовлетворяет условию целочисленности. Поэтому вновь требуется составить дополнительное условие. В данном случае можно использовать первое или третье уравнение. Получится следующее дополнительное условие:
. Этот план, как и предыдущий, не удовлетворяет условию целочисленности. Поэтому вновь требуется составить дополнительное условие. В данном случае можно использовать первое или третье уравнение. Получится следующее дополнительное условие:
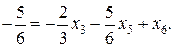
Составляем следующую таблицу:
| Таблица 6 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X4 | |||
| X1 | 17/6 | 2/3 | -1/6 | 1/7 |
| X2 | 1/3 | -1/3 | 1/3 | -2/7 |
| X4 | 5/6 | 2/3 | -7/6 | |
| X6 | -5/6 | -2/3 | -5/6 | |
| С | 55/6 | 4/3 | 1/6 | -1/7 |
Оптимальный план 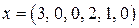 получаем из следующей, завершающей таблицы:
получаем из следующей, завершающей таблицы:
| Таблица 7 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X3 | X6 | |||
| X1 | 4/5 | -1/5 | 1/6 | |
| X2 | -3/5 | 2/5 | -1/3 | |
| X4 | 8/5 | -7/5 | 7/6 | |
| X5 | 4/5 | -6/5 | ||
| С | 6/5 | 1/5 | -1/6 |
Так как найденный оптимальный план удовлетворяет условию целочисленности, задача целочисленного программирования решена. Координаты x5 и x6 можно не учитывать, так как начальные условия задачи содержит лишь четыре неизвестные. Поэтому окончательный оптимальный план запишется так: 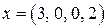 , а максимум функции цели равен 9.
, а максимум функции цели равен 9.
Дата добавления: 2021-07-22; просмотров: 628;











