Метод ветвей и границ решения задач целочисленного программирования
Методом ветвей и границ удобно решать такие задачи целочисленного программирования, в которых число неизвестных невелико либо требования целочисленности относятся не ко всем неизвестным. Суть метода ветвей и границ состоит в том, что для тех неизвестных, к которым относится требование целочисленности, нужно определить границы, в которых могут находиться значения этих неизвестных. Затем решаются соответствующие задачи линейного программирования.
Задание границ, в которых должны находиться значения неизвестных в задаче целочисленного программирования, можно записать так: 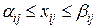 .
.
На практике во многих случаях границы значений неизвестных уже включены в систему ограничений задачи целочисленного программирования или же их можно определить исходя из экономического содержания задачи. Иначе можно принять, что нижняя граница 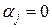 , а верхняя граница
, а верхняя граница 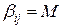 , где M - достаточно большое положительное число.
, где M - достаточно большое положительное число.
Как метод ветвей и границ позволяет уточнить границы допустимых значений неизвестных?
Сначала решается, допустим, симплекс-методом задача линейного программирования, соответствующая задаче целочисленного программирования. Пусть найден оптимальный план в этой задаче и значением какой-либо его координаты 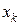 является дробное число. Тогда потребуется составить две новые задачи линейного программирования. Как это сделать?
является дробное число. Тогда потребуется составить две новые задачи линейного программирования. Как это сделать?
Обозначим целую часть координаты 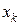 в виде
в виде 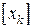 . В одной из новых задач линейного программирования нижней границей значения координаты
. В одной из новых задач линейного программирования нижней границей значения координаты 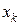 будет число
будет число 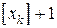 , то есть целая часть значения координаты, увеличенная на единицу. Это запишется следующим образом:
, то есть целая часть значения координаты, увеличенная на единицу. Это запишется следующим образом: 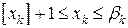 .
.
В другой новой задаче линейного программирования верхней границей значения координаты 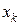 будет сама целая часть
будет сама целая часть 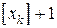 значения координаты
значения координаты 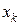 . Это запишется так:
. Это запишется так: 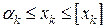 .
.
Таким образом, от первой задачи линейного программирования "ответвились" две новые задачи, в которых в которых изменились границы допустимых значений одной неизвестной. При решении каждой из этих задач возможны три случая:
· оптимальный план не является целочисленным,
· оптимальный план является целочисленным,
· задача не имеет решений.
Лишь в первом случае возможно "ответвление" новых задач способом, показанным выше. Во втором и третьем случае "ветвление" прекращается.
На каждой итерации решения задачи целочисленного программирования решается одна задача. Введём понятие: список решаемых задач линейного программирования. Из списка следует выбрать задачу, решаемую на соответствующей итерации. На дальнейших итерациях список меняется, так как решённые задачи в него уже не входят, а вместо них в список включаются новые задачи, которые "ответвились" от предыдущих задач.
Для того, чтобы ограничить "ветвления", то есть уменьшить число решаемых задач, на каждой итерации следует определить нижнюю границу максимального значения целевой функции. Это делается следующим образом:
· если задача задана в нормальной форме, то перед её решением нижняя граница имеет значение нуль (то есть 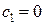 );
);
· если на некоторой итерации (назовём её p-й) найденный план не является целочисленным и максимальное значение целевой функции больше ранее установленной нижней границы, то на следующей итерации нижняя граница максимального значения целевой функции остаётся прежней (как на предыдущей итерации, то есть 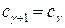 );
);
· если на некоторой итерации найденный план 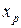 является целочисленным и максимальное значение целевой функции, найденное вместе с этим планом
является целочисленным и максимальное значение целевой функции, найденное вместе с этим планом 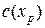 , больше ранее установленной нижней границы, то для следующей итерации устанавливается новая нижняя граница, то есть
, больше ранее установленной нижней границы, то для следующей итерации устанавливается новая нижняя граница, то есть 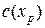 переходит на следующую итерацию;
переходит на следующую итерацию;
· если на некоторой итерации максимальное значение целевой функции, найденное вместе с этим планом 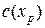 , меньше ранее установленной нижней границы, то нижняя граница остаётся прежней.
, меньше ранее установленной нижней границы, то нижняя граница остаётся прежней.
Согласно алгоритму решения задачи целочисленного программирования методом ветвей и границ, на каждой p-й итерации требуется сделать 4 шага.
· Шаг 1. Если в списке решаемых задач нет ни одной задачи, то задача целочисленного программирования решена. Максимальное значение функции цели - то, которое было найдено на предыдущей итерации, оптимальный план - целочисленный план, найденный на предыдущей итерации. В противном случае следует выбрать одну из задач, имеющихся в списке.
· Шаг 2. Решается выбранная из списка задача линейного программирования. Если задача не имеет решения или для полученного на этом шаге оптимального плана 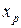 значение функции цели
значение функции цели 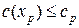 , то следует принять
, то следует принять 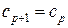 и выполнить шаг 1. В противном случае выполнять шаг 3.
и выполнить шаг 1. В противном случае выполнять шаг 3.
· Шаг 3. Если найденный оптимальный план 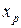 является целочисленным, то следует принять, что
является целочисленным, то следует принять, что 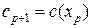 и выполнить шаг 1. В противном случае выполнить шаг 4.
и выполнить шаг 1. В противном случае выполнить шаг 4.
· Шаг 4. Выбрать любую дробную координату оптимального плана 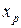 . Определить целую часть координаты, составить две новые задачи линейного программирования и включить их в список решаемых задач. Новые задачи отличаются от задачи, выбранной на шаге 1 только границами допустимых значений выбранной координаты. Принять, что
. Определить целую часть координаты, составить две новые задачи линейного программирования и включить их в список решаемых задач. Новые задачи отличаются от задачи, выбранной на шаге 1 только границами допустимых значений выбранной координаты. Принять, что 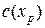 и выполнить шаг 1.
и выполнить шаг 1.
Пример. Решить методом ветвей и границ следующую задачу целочисленного программирования. Найти максимум целевой функции 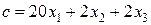 при системе ограничений
при системе ограничений
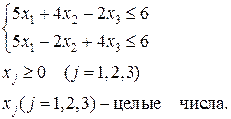
Решение. Допустим, что заданы или определены следующие границы оптимальных значений неизвестных:
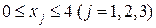
Так как задача задана в нормальной форме, она имеет целочисленный план 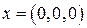 и нижнюю границу максимального значения целевой функции
и нижнюю границу максимального значения целевой функции 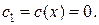
В списке решаемых задач - 1-я задача:
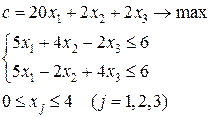
Итерация 1.
Шаг 1. С помощью симплекс-метода получено решение 1-й задачи:
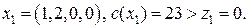
Так как найденный план не является целочисленным, следует шаг 4.
Шаг 4. Так как оптимальный план 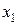 имеет дробную координату 1,2, то
имеет дробную координату 1,2, то 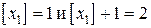 . Применяя границы значений неизвестных 1-й задачи, получаем новые задачи. Во 2-й задаче нижней границей для
. Применяя границы значений неизвестных 1-й задачи, получаем новые задачи. Во 2-й задаче нижней границей для 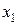 является
является 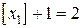 , а в 3-й задаче верхней границей для
, а в 3-й задаче верхней границей для 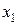 является
является 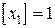 .
.
Итак, следует решить 2-ю задачу:
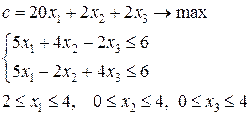
и 3-ю задачу:
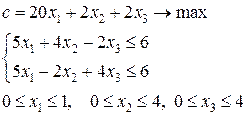
Нижняя граница максимального значения целевой функции 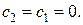
Итерация 2.
Шаг 1. Из списка решаемых задач выбираем 2-ю задачу.
Шаг 2. Констатируем, что 2-я задача не имеет решения, так как её система ограничений несовместна. Тогда 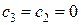 и следует следующая итерация.
и следует следующая итерация.
Итерация 3.
Шаг 1. В списке имеется только одна - 3-я задача.
Шаг 2. Применяя симплекс-метод, получаем решение 3-й задачи:
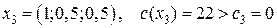
Так как это решение не является целочисленным, следует шаг 4.
Шаг 4. Выбираем дробную координату 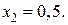 Тогда
Тогда 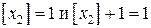 . Применяя границы значений неизвестных из 3-й задачи, получаем две новых задачи.
. Применяя границы значений неизвестных из 3-й задачи, получаем две новых задачи.
4-я задача:
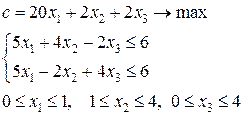
5-я задача:
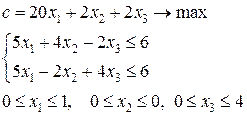
Нижняя граница максимального значения функции цели 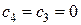 .
.
Итерация 4.
Шаг 1. Из списка решаемых задач, в котором имеются 4-я и 5-я задачи, выбираем 4-ю задачу.
Шаг 2. Применяя симплекс-метод, получаем решение 4-й задачи:
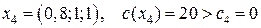
Так как полученное решение не является целочисленным, следует шаг 4.
Шаг 4. Выбираем дробную координату 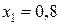 и получаем
и получаем 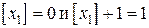 . Применяя границы значений переменной
. Применяя границы значений переменной 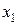 , получаем две новые задачи линейного программирования.
, получаем две новые задачи линейного программирования.
6-я задача:
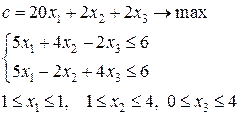
7-я задача:
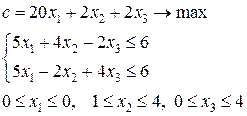
Итак, в списке решаемых задач имеются 5-я, 6-я и 7-я задачи, а нижняя граница максимального значения функции цели 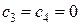 .
.
Итерация 5.
Шаг 1. Из списка выбираем 5-ю задачу.
Шаг 2. Применяя симплекс-метод, получаем решение 5-й задачи:
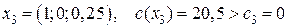
Так как найденный план не является целочисленным, следует шаг 4.
Шаг 4. Выбираем дробную координату 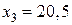 и получаем
и получаем 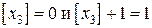 . Применяя границы значений неизвестной
. Применяя границы значений неизвестной 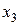 5-й задачи, получаем две новые задачи.
5-й задачи, получаем две новые задачи.
8-я задача:
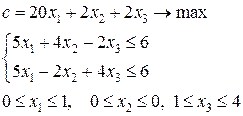
9-я задача:
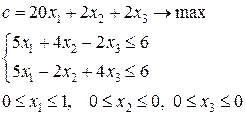
В списке решаемых задач имеются 6-я, 7-я, 8-я и 9-я задачи, а нижняя граница максимального значения функции цели 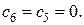
Итерация 6.
Шаг 1. Из списка решаемых задач выбираем 6-ю задачу.
Шаг 2. Констатируем, что 6-я задача не имеет решения. Поэтому нижняя граница максимального значения функции цели 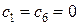 и следует следующая итерация.
и следует следующая итерация.
Итерация 7.
Шаг 1. Из списка решаемых задач выбираем 7-ю задачу.
Шаг 2. Применяя симплекс-метод, получаем решение 7-й задачи:
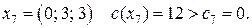
Шаг 3. Так как полученное решение является целочисленным, то нижняя граница максимального значения функции цели 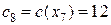 и далее следует итерация 8.
и далее следует итерация 8.
Итерация 8.
Шаг 1. Из списка решаемых задач выбираем 8-ю задачу.
Шаг 2. Применяя симплекс-метод, получаем решение 8-й задачи:
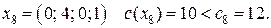
Нижняя граница максимального значения функции цели 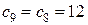 , далее - следующая итерация.
, далее - следующая итерация.
Итерация 9.
Шаг 1. В списке решаемых задач имеется лишь 9-я задача.
Шаг 2. Применяем симплекс-метод и получаем решение 9-й задачи:
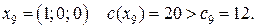
Шаг 3.Так как полученное решение является целочисленным, нижняя граница максимального значения функции цели 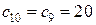 и переходим к следующей итерации.
и переходим к следующей итерации.
Итерация 10.
Шаг 1. В списке решаемых задач нет ни одной задачи. Таким образом, решение данной задачи целочисленного программирования следующее:
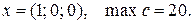
Дата добавления: 2021-07-22; просмотров: 520;











