Дифференциальные уравнения движения идеальной жидкости
(уравнения Эйлера)
Формально общие уравнения движения идеальной жидкости можно получить из уравнений, составленных для покоящейся жидкости, если воспользоваться принципом Д. Аламбера, согласно которому к уже действующим силам добавляются силы инерции.
Обозначим силу инерции, отнесенную к единице массы движущейся идеальной жидкости 1 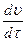 . Тогда проекции этой силы на координатные оси будут равны: -1
. Тогда проекции этой силы на координатные оси будут равны: -1 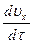 ; -1
; -1 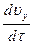 и -1
и -1 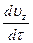 . Знак минус в данном случае указывает на то, что единичная сила инерции имеет направление противоположное ускорению.
. Знак минус в данном случае указывает на то, что единичная сила инерции имеет направление противоположное ускорению.
С учетом сказанного дифференциальные уравнения движения идеальной жидкости получает вид:
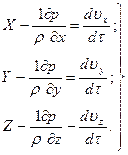 (56)
(56)
Для случая неустановившегося движения, когда 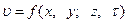 полный дифференциал скорости, например
полный дифференциал скорости, например 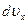 , равен
, равен
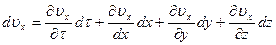 ,
,
тогда
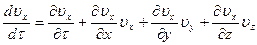 .
.
С учетом аналогичных выражений, полученных для 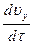 и
и 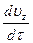 , дифференциальные уравнения неустановившегося движения идеальной жидкости получают следующий вид:
, дифференциальные уравнения неустановившегося движения идеальной жидкости получают следующий вид:
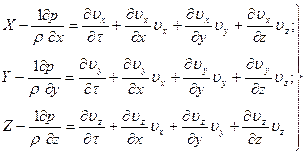 (57)
(57)
Для установившегося движения идеальной жидкости, когда 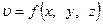 , дифференциальные уравнения движения идеальной жидкости имеют вид
, дифференциальные уравнения движения идеальной жидкости имеют вид
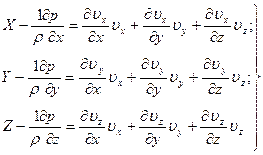 (58)
(58)
Системы дифференциальных уравнений (57) и (58) называются системами дифференциальных уравнений движения идеальной жидкости, представленными в развернутом виде.
Уравнения (56) – (58) применимы как для случаев движения капельных жидкостей (когда 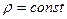 ), так и для движения газов (когда
), так и для движения газов (когда 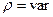 ).
).
Дата добавления: 2017-05-02; просмотров: 1161;











