ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ И ИНДУКТИВНОСТЬ СИСТЕМЫ
Определим энергию в электромагните при неподвижном якоре и при включении катушки на напряжение постоянного тока. Ток в ней установится не мгновенно, а по некоторой кривой (рис. 5-2). Приложенное к катушке напряжение U в переходном процессе уравновешивается активным падением напряжения ir и ЭДС самоиндукции е:
U = ir + e.m (5.1)
ЭДС самоиндукции пропорциональна скорости изменения потокосцепления обмотки:
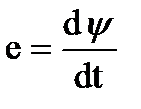 (5.2)
(5.2)
Умножив уравнение (5-1) на idt и взяв интеграл, получим энергетический баланс электромагнита за время переходного процесса:
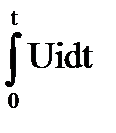 -
- 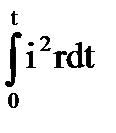 =
= 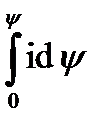 , (5-3)
, (5-3)
где 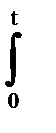 Uidt — энергия, поступившая из сети;
Uidt — энергия, поступившая из сети; 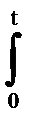 i2rdt — потери энергий в катушке
i2rdt — потери энергий в катушке
электромагнита; 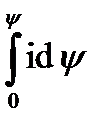 = WM — энергия, сообщенная электромагниту.
= WM — энергия, сообщенная электромагниту.
Таким образом, энергия, сообщенная электромагниту, равна энергии, поступившей из сети, за вычетом потерь в катушке и магнитопроводе.
При установившемся режиме Uidt = i2rdt, т. е. вся поступающая из сети энергия расходуется на потери в катушке.
Говоря о потокосцеплении  ,следует иметь в виду, что его значение является сложной функцией тока. Зависимость
,следует иметь в виду, что его значение является сложной функцией тока. Зависимость 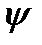 =
=  Ф = f(i) представлена на рис. 5-3. Она учитывает нелинейность кривой намагничивания для стали и зависит от тока, материала и размеров магнитопровода и воздушного зазора. Запасенная в электромагните энергия на графике пропорциональна площади, ограниченной
Ф = f(i) представлена на рис. 5-3. Она учитывает нелинейность кривой намагничивания для стали и зависит от тока, материала и размеров магнитопровода и воздушного зазора. Запасенная в электромагните энергия на графике пропорциональна площади, ограниченной
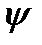 = f(t) и осью ординат (заштрихованная площадь).
= f(t) и осью ординат (заштрихованная площадь).
Как известно, отношение
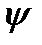 /I = L, (5-4)
/I = L, (5-4)
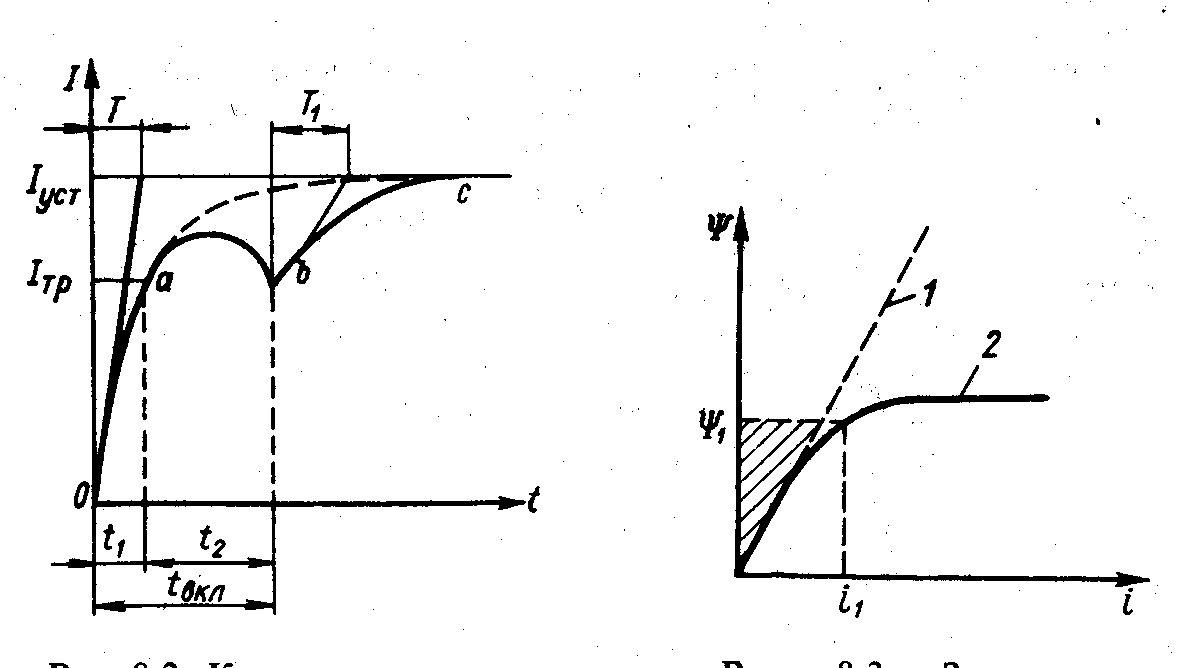
Рис. 5-2. Кривая нарастания Рис. 5-3. Зависимость
тока в катушке при включе- 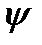 = f(i)
= f(i)
нии электромагнита постоян- 1 — в цепи без стали; 2 —
ного тока в цепи со сталью
где I — ток в катушке; L представляет собой индуктивность системы. Для системы со сталью (кривая 2 на рис. 5-3) индуктивность не является постоянной величиной, а зависит от степени насыщения системы. Каждому значению потоко-сцепления будут соответствовать какая-то индуктивность и определенное значение запасенной энергии, т. е.
WM = 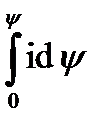 =
= 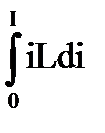 = L
= L 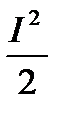 , (5.5)
, (5.5)
откуда L= 2Wм/I2.
Дата добавления: 2017-05-02; просмотров: 2262;











