Решение двух плоских задач для установившегося притока к горизонтальной скважине

Рассмотрим стационарный приток несжимаемой жидкости к горизонтальной скважине длины 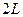в однородном изотропном пласте проницаемости 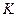с продуктивной толщиной 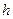и непроницаемой кровлей и подошвой. Для простоты предположим, что скважина расположена в центре пласта. Будем считать справедливым закон Дарси. На забое скважины поддерживается постоянное забойное давление 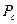, а на удаленном контуре питания радиуса 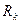постоянное пластовое давление 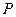[28].

Определение дебита или коэффициента продуктивности горизонтальной скважины сводится к решению трехмерного уравнения Лапласа для давления с соответствующими краевыми условиями и не имеет простого аналитического решения. В связи с этим для получения простой расчетной формулы для дебита обычно используется следующий приближенный прием. Исходная пространственная задача сводится к решению двух плоских задач (рис. 1.2):

· течению жидкости в горизонтальной плоскости к линейному стоку, представляющему собой очень тонкую пластину;

· приток жидкости к точечному стоку вертикальной плоскости с непроницаемой кровлей и подошвой.

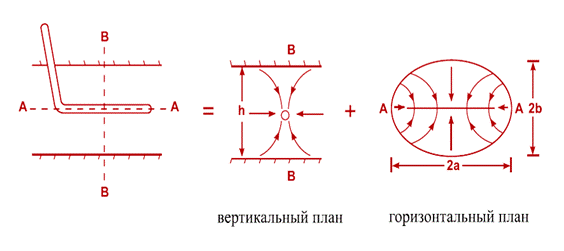
Рис. 1.2. Разделение трехмерной задачи на две двухмерные

Из первой плоской задачи определяется внешнее фильтрационное сопротивление, а из второй – внутреннее фильтрационное сопротивление.

Первый тип потока в дальнейшем для простоты будем именовать эллиптическим, учитывая, что изобары имеют вид эллипса. Суммарная производительность горизонтальной скважины рассчитывается как суперпозиция соответствующих решений этих двух плоских задач.

Существующие методы для определения дебита или коэффициента продуктивности горизонтальной скважины, в основу которых положен отмеченный выше подход, в основном отличается решениями для установившегося течения жидкости к точечному и линейному стоку.

Наиболее общее решение для эллиптического потока можно получить при использовании двумерного уравнения Лапласа с заменой потенциала течения на давление:

. (1.48)

Одной из самых простых формул для эллиптического потока является зависимость Джоши:

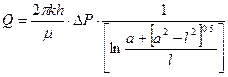, (1.49)

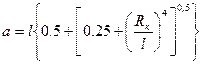. (1.50)

Для описания течения к точечному стоку с дебитом Q используется уравнение Дюпии для радиального потока, в котором толщина пласта заменена длиной горизонтального ствола, а радиус контура питания Rk – половиной толщины пласта:

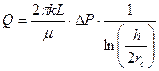. (1.51)

Результирующий дебит для горизонтальной скважины находится суммированием фильтрационных сопротивлений, соответствующих каждой из плоских задач. Соответствующая формула имеет вид:

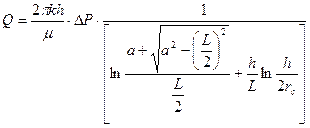. (1.52)

Параметр 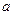в формуле представляет собой то же самое, что и радиус контура питания 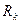в известной формуле Дюпии, то есть характеризует границу, на которой поддерживается постоянное давление. Определение данных величин для реальных скважин возможно с большой степенью приближения.

Учитывая, что большинство специалистов привыкло к использованию 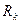, Джоши приводит следующую приближенную формулу для определения параметра :

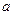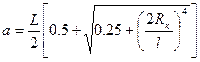. (1.53)

При описании эллиптического потока Борисов положил другое условие для определения 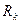. В качестве данной величины используется основной радиус эллипса, представляющий собой среднюю величину между полуосями:

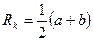(1.54)

Выражение для Q имеет вид:

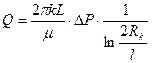(1.55)

Общая формула для притока к горизонтальной скважине, полученная Борисовым, имеет следующий вид:

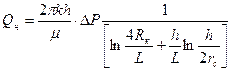(1.56)

Можно заметить, что приток к точечному стоку в полосе шириной 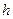определяется по иной формуле по сравнению с (1.51). В отличие от упрощенного подхода Джоши (1.52), в данном случае рассматривается влияние непроницаемых кровли и подошвы пласта. Задача решается при использовании метода суперпозиций путем введения бесконечного числа фиктивных скважин, отраженных относительно кровли и подошвы.

Учет влияния непроницаемых границ пласта является более точным подходом к решению задачи притока жидкости к точечному стоку в полосе шириной .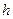

Таким образом, при получении расчётных формул дебита или продуктивности горизонтальной скважины обычно используют замену исходной пространственной задачи решением двух плоских задач – течению к очень тонкой пластине в горизонтальной области и притоку к точечному стоку в полосе шириной 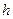в вертикальной области. Уравнения, описывающие течение к тонкой пластине при моделировании в горизонтальной плоскости, с достаточной точностью можно применить к описанию горизонтальных скважин. В большинстве случаев авторы пытались ввести в рассмотрение радиус контура питания, вводя при этом определенные допущения. Однако, наиболее точно процесс фильтрации описывается при использовании полуосей эллипса, которые для реальных условиях можно оценить только ориентировочно, как и радиус контура питания для вертикальной скважины. При описании течения к точечному стоку в полосе наибольшая точность достигается при учете влияния непроницаемых кровли и подошвы по сравнению с радиальным потоком. Поток к горизонтальной скважине имеет наибольшее значение на концах ствола и минимальное в середине.