Тренировочное задание

Постановка и решение транспортной задачи методом "северо-западного угла".

Любая транспортная задача может быть формализованно описана следующим образом.

Имеется m поставщиков определенного вида продукции (либо m– количество мест, складов, откуда происходит поставка продукции). Максимальные объемы возможных поставок заданы и равны соответственно a_i, i = 1, 2, ..., m. Эта продукция используется n потребителями. Объемы потребностей заданы и равны соответственно b_j, j=1, 2, ... , n. Стоимость перевозки единицы продукции от i-го поставщика к j-му потребителю известна для всех i, j и равна c_ij. Требуется установить такие объемы перевозок x_ij от каждого поставщика к каждому потребителю, чтобы суммарные затраты на перевозки были минимальными и потребности всех потребителей были бы удовлетворены (если только общий объем возможных поставок покрывает общий объем потребностей).

ЗАДАЧА 1.

На двух складах А и В имеется соответственно 50 и 40 тонн груза. Требуется спланировать перевозки к трем потребителям C, D и E так, чтобы потребитель C получил 30 тонн груза, D – 20 тонн, E – 40 тонн, а затраты на перевозку были минимальными. Стоимость перевозки от складов к потребителям приведена в таблице 7.2 в правых верхних углах каждой клетки. Например, стоимость перевозки единицы (1 тонны) груза со склада А потребителю С равна 3 усл. единицы.

Для решения такой задачи на первом этапе составляется система ограничений и целевая функция.

Система ограничений в общем виде для нашей задачи имеет следующий вид:

,

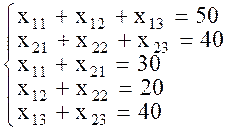причем х_ij>0 для i=1,2; j=1,2,3.

Таблица 7.2

Исходные данные для решения транспортной задачи

Потребители   Склады	С	D	E	Наличие груза на складах
А	X11	X12	X13
В	X21	X22	X23
Потребности потребителей

Целевая функция затрат на перевозку, значение которой необходимо минимизировать при имеющихся ограничениях, имеет вид:

F = 3х₁₁ + 2х₁₂ + х₁₃ + 3х₂₁ + 5х₂₂ + 6х₂₃.

Далее делается первое распределение объемов поставок грузов методом "северо-западного угла" (первой заполняется верхняя левая (северо-западная) клетка исходной таблицы. Примем объем перевозки со склада А к потребителю С максимально возможным из условий задачи и равным 30 тоннам. Потребитель С полностью удовлетворил свою потребность, и столбец "С" в таблице 2 можно исключить из дальнейшего рассмотрения.

В таблице поставок найдем северо-западный угол – теперь это клетка AD, и укажем в ней максимально возможное значение, которое рассчитывается следующим образом: со склада А уже перевезено 30 тонн груза, значит остаток на складе составляет 50-30=20 тонн. Вносим в клетку AD вместо х₁₂значение, равное 20 тоннам. Таким образом, весь груз со склада А перевезен потребителям, и первая строка таблицы поставок исключается из дальнейшего рассмотрения. Потребитель D полностью удовлетворил свою потребность в грузе, и столбец D можно исключить из дальнейшего рассмотрения. В оставшейся части таблицы найдем новый северо-западный угол – это клетка BE, и укажем в ней максимально возможное значение (40 тонн). Итак, в таблице 7.3 отражено исходное распределение поставок: х₁₁=30; х₁₂=20; х₂₃=40.

Таблица 7.3

Исходное распределение поставок

Потребители   Склады	С	D	E	Наличие груза на складах
А
В
Потребности потребителей

В результате получим следующее значение целевой функции:

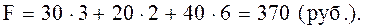
Дальнейшие вычисления направлены на получение оптимального минимального значения целевой функции F (Практикум по логистике: Учеб. пособие/Под ред. Б.А. Аникина. М.: ИНФРА-М, 1999. С.222). Они достаточно громоздки и в большинстве случаев реализуются на основе применения программного обеспечения. Для использования программных вычислений необходимо ввести в качестве исходных данных систему ограничений и сделать первое распределение поставок.