Тема: ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ.

Основными термодинамическими процессами являются:

1) Изохорный процесс - процесс сообщения или отнятия теплоты при постоянном объёме газа (V=const);

2) Изобарный процесс - процесс сообщения или отнятия теплоты при постоянном давлении (Р=const);

3) Изотермический процесс - процесс сообщения или отнятия теплоты при постоянной температуре (t=const);

4) Адиабатный процесс – процесс, при котором отсутствует теплообмен с окружающей средой (dq=0);

5) Политропный процесс - процесс, в котором изменение параметров подчиняется уравнению 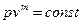, где m - величина, постоянная для данного процесса

Метод исследования процессов состоит в следующем:

1. Выводится уравнение процесса, устанавливающее связь между начальными и конечными параметрами рабочего тела в данном процессе;

2. Вычисляется работа изменения объема газа;

3. Определяется количество теплоты, подведенной (или отведенной) к газу в процессе;

4. Определяется изменение внутренней энергии системы в процессе;

5. Определяется изменение энтропии системы в процессе.

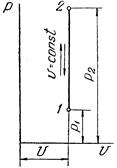
1 Изохорный процесс (V=const)

Для графического метода исследования процессов используется координатная система p-v.

Изохорный процесс в pv-диаграмме изображается отрезком прямой 1-2, идущим параллельно оси ординат. Прямая 1-2 называется изохорой.

При направлении от точки 1 к точке 2 процесс идёт с сообщением теплоты, при направлении от точки 2 к точке 1 – с отводом теплоты.

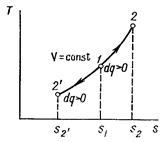Рисунок 1 – Изохорный процесс в pv- и TS-диаграмме

Уравнение изохоры имеет вид 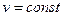, (1)

Зависимость между начальными и конечными параметрами процесса выражается

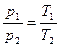, (2)

Изменение внутренней энергии определяется

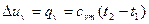, (3)

Если в процессе участвует М, кг или V_н, м³ газа, то количество теплоты (изменение внутренней энергии газа) определяется

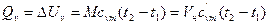, (4)

где 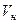- количество газа при нормальных условиях, м³.

Если количество теплоты необходимо подсчитать, пользуясь нелинейной зависимостью теплоёмкости от температуры, то применяют следующие формулы:

- количество теплоты, затрачиваемой для нагревания 1кг газа в интервале температур от t₁ до t₂при постоянном объёме

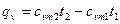, (5)

- если в процессе участвуют М, кг или V_н, м³ газа, то

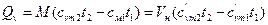, (6)

В изохорном процессе из-за отсутствия расширения газа работа L=0, и подводимая к газу теплота полностью идёт на изменение его внутренней энергии.

Изменение энтропии в изохорном процессе 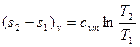(7)

2 Изобарный процесс (Р=const)

Изобарный процесс в pv-диаграмме изображается отрезком прямой 1-2, идущим параллельно оси абсцисс. Прямая 1-2 называется изобарой.

При направлении от точки 1 к точке 2 процесс идёт с сообщением теплоты. Работа в этом случае имеет положительное значение. При направлении от точки 2 к точке 1 – с отводом теплоты, и работа имеет отрицательное значение.

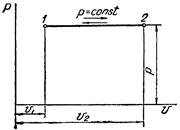Рисунок 2 – Изобарный процесс в pv- и TS-диаграмме

Уравнение изобары имеет вид 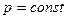, (8)

Зависимость между начальными и конечными параметрами процесса выражается

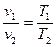, (9)

Работа 1кг газа определяется по формуле

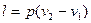, (10)

или 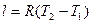, (11)

Для М, кг газа работа определяется

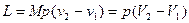, (12)

или 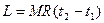, (13)

где 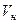- количество газа при нормальных условиях, м³.

Если количество теплоты необходимо подсчитать, пользуясь нелинейной зависимостью теплоёмкости от температуры, то применяют формулы

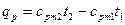, (14)

- если в процессе участвуют М, кг или V_н, м³ газа, то

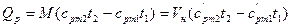, (15)

Изменение внутренней энергии определяется

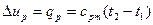, (16)

Изменение энтропии в изобарном процессе

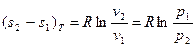(17)

3 Изотермический процесс (t=const)

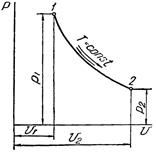
Изотермический процесс в pv-диаграмме изображается равнобокой гиперболой 1-2, для которой координатные оси служат асимптотами. Гипербола 1-2 называется изотермой.

При направлении от точки 1 к точке 2 процесс идёт с сообщением теплоты. Работа в этом случае имеет положительное значение. При направлении от точки 2 к точке 1 – с отводом теплоты, и работа имеет отрицательное значение.

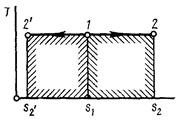Рисунок 3 – Изотермический процесс в pv- и TS-диаграмме

Уравнение изотермы имеет вид 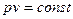, (18)

Зависимость между начальными и конечными параметрами процесса выражается

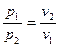, (19)

Работа 1кг идеального газа определяется уравнениями

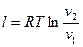, (20)

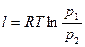, (21)

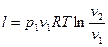, (22)

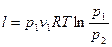, (23)

Так как в изотермическом процессе t=const, то изменение внутренней энергии определяется 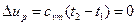, (24)

Количество теплоты, сообщаемой газу или отнимаемой от него, определяется

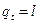, (25)

для М, кг газа 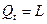, (26)

Натуральный логарифм, входящий в формулы, может быть заменён десятичным по соотношению lgN = 2,303 lgN. 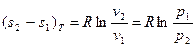(27)

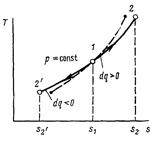
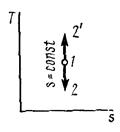
4 Адиабатный процесс (dq=0)

Основным условием адиабатного процесса является полное отсутствие теплообмена между средой и рабочим телом (газом). Адиабатный процесс в pv-диаграмме изображается неравнобокой гиперболой 1-2, не пересекающую координатных осей. Гипербола называется адиабатой. Адиабата располагается круче изотермы.

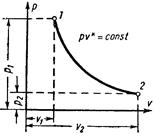Рисунок 4 – Адиабатный процесс в pv- и TS-диаграмме

Уравнение адиабаты имеет вид 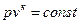, где 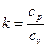- показатель адиабаты. (28)

Зависимость между начальными и конечными параметрами процесса:

между p и v 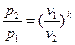, (29)

между Т и v 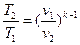, (30)

между p и T 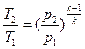, (31)

Работа 1кг газа определяется по следующим формулам

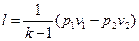, (32)

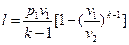, (33)

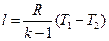, (34)

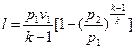, (35)

Уравнение первого закона термодинамики для адиабатного процесса имеет вид

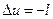, (36)

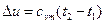, (37)

Изменение внутренней энергии газа и работа адиабатного процесса равны по величине и противоположны по знаку.

Изменение энтропии в адиабатном процессе

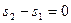, s=const (38)

5 Политропный процесс ( )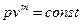

Политропным процессом описывается любой закономерный процесс или совокупность отдельных закономерных процессов.

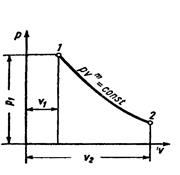Рисунок 5 – Политропный процесс в pv- диаграмме

Уравнение политропыпри постоянной теплоёмкости имеет вид

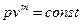, (39)

где m - показатель политропы.

Характеристикой политропного процесса является величина

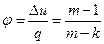, (40)

где .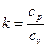

По величине показателя политропы m можно определить её относительное расположение в pv-диграмме и выяснить характер процесса, т.е. есть ли подвод или отвод теплоты, увеличение или уменьшение внутренней энергии газа.

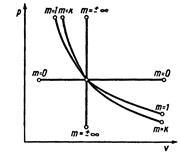Для процессов расширения:

1) m>1 – теплота подводится (q>0), внутренняя энергия газа увеличивается ( 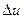>0);

2) к>m>1 – теплота подводится (q>0), внутренняя энергия газа уменьшается ( 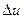<0);

3) m>к – теплота отводится (q<0), внутренняя энергия газа уменьшается ( 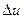<0).

Для процессов сжатия:

1) m<1 – теплота отводится, внутренняя энергия газа уменьшается;

2) к>m>1 – теплота отводится, внутренняя энергия газа увеличивается;

3) m>к – теплота подводится, внутренняя энергия газа увеличивается.

Зависимость между начальными и конечными параметрами процесса:

между p и v 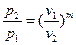, (41)

между Т и v 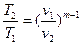, (42)

между p и T 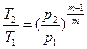, (43)

Работа 1кг газа определяется по следующим формулам

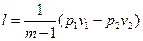, (44)

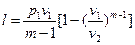, (45)

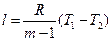, (46)

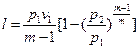, (47)

Если количество теплоты, участвующей в процессе, известно, то работа может быть определена 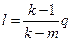, (48)

Теплоёмкость политропного процесса определяется 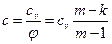, (49)

Количество теплоты, сообщаемой газу или отнимаемой от него, определяется

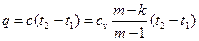, (50)

Изменение внутренней энергии газа определяется

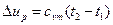, (51)

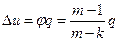, (52)

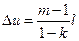, (53)

Показатель политропного процесса определяется 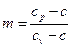, (54)

Изменение энтропии в политропном процессе

s₂ –s₁= c ln T₂/ T₁ , где c = c_v[ (m-k) / (m-1) ] (55)

ЛЕКЦИЯ № 8

<5 6 789 10 11 >

Дата добавления: 2021-07-22; просмотров: 327;