Задачи оптимального резервирования (темпоральные задачи о ранце).
Задачи оптимального резервирования возникают при оптимальном управлении ресурсами, распределенными во времени[2], аналогичные последним темпоральные задачи о ранце[3] получили в последнее время применение при решении задач предварительного резервирования вычислительных ресурсов в Grid Computing[4] и имеют следующий вид:
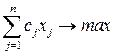 (3.1)
(3.1)
при ограничениях
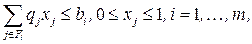 (3.2)
(3.2)
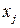 ‑ целое,
‑ целое, 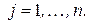 (3.3)
(3.3)
Здесь 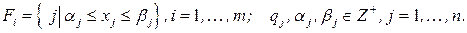
Матрица ограничений этой задачи является квазиблочной и называется обобщенной матрицей Петри (ОМП) (см. рис. 3.1). Как известно, недостатками симплекс-метода при решении задач ЛП являются ошибки округления (возникающие в результате деления) и вызываемая этим необходимость пересчета обратной матрицы. Покажем, что при решении линейных релаксаций (3.1) ‑ (3.2) рассматриваемой задачи ДО с этими трудностями мы не столкнемся. Для этого установим следующее простое утверждение:
Утверждение 3.1.Детерминант обобщенной матрицы Петри размерности 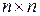
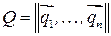 равен
равен 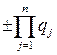 или 0.
или 0.
Доказательство проведем, используя метод математической индукции.
П.1. При 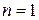 утверждение справедливо.
утверждение справедливо.
П.2. Предположим, что оно справедливо при 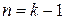 . Докажем, что оно справедливо и при
. Докажем, что оно справедливо и при 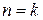 .
.
строке матрицы 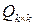 находятся числа
находятся числа 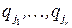 . Далее могут встретиться случаи:
. Далее могут встретиться случаи:
a) среди чисел 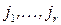 есть одинаковые. В этом случае
есть одинаковые. В этом случае 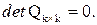
b) среди чисел 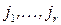 нет одинаковых. Тогда с помощью элементарных преобразований над столбцами матрицы, не изменяющих определитель, можно добиться того, что последняя строка матрицы
нет одинаковых. Тогда с помощью элементарных преобразований над столбцами матрицы, не изменяющих определитель, можно добиться того, что последняя строка матрицы 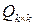 будет иметь вид
будет иметь вид 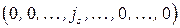 , где
, где 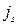 ‑ номер столбца с минимальной длиной. Далее, при вычислении
‑ номер столбца с минимальной длиной. Далее, при вычислении 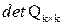 , можно разложить детерминант по элементам последней строки:
, можно разложить детерминант по элементам последней строки: 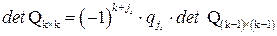 , где
, где 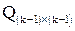 ‑ ОМП
‑ ОМП 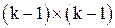 , полученная путем отбрасывания последней строки матрицы
, полученная путем отбрасывания последней строки матрицы 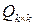 и
и 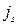 -го столбца. Согласно предположению,
-го столбца. Согласно предположению, 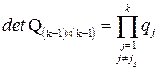 или 0.
или 0.
Из последнего утверждения и следует справедливость утверждения 3.1.
Следствие 3.1. Если ОМП 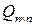 невырождена, то элементы строки
невырождена, то элементы строки 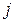 обратной матрицы
обратной матрицы 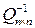 имеют вид
имеют вид 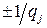 или 0.
или 0.
|

Таким образом, при пересчете обратной матрицы на каждом шаге модифицированного симплекс-метода не нужно пользоваться операциями умножения и деления, которые и порождают ошибки округления, можно пользоваться лишь операциями сложения и вычитания, причем обратную матрицу можно хранить в памяти в виде целых чисел 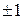 или 0, так как знаменатели
или 0, так как знаменатели 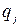 определяются однозначно.
определяются однозначно.
В результате, во-первых, предъявляются гораздо более скромные требования к памяти компьютера за счет экономного хранения обратной матрицы, во-вторых, за счет применения лишь аддитивных операций при пересчете обратной матрицы время счета уменьшается, в-третьих, нет ошибок округления, и вследствие этого нет необходимости находить уточненные элементы обратной матрицы.
Следствие 3.2. Матрица Петри унимодулярна (ОМП при 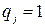 ).
).
Отсюда следует, что рассматриваемую задачу ДО в случае 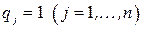 можно решать как линейную задачу (3.1) ‑ (3.2) с помощью алгоритма линейного программирования, например, симплекс-метода.
можно решать как линейную задачу (3.1) ‑ (3.2) с помощью алгоритма линейного программирования, например, симплекс-метода.
Замечание. Обратная матрица ОМП находится достаточно просто. Согласно следствию 3.1 достаточно найти обратную матрицу при 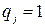 с помощью следующего алгоритма. К матрице Петри снизу дописывается единичная матрица, и производятся следующие преобразования полученной матрицы: если какие-либо два столбца матрицы Петри имеют одинаковое начало и конец, из более длинного столбца нужно вычесть более короткий, т.е. если
с помощью следующего алгоритма. К матрице Петри снизу дописывается единичная матрица, и производятся следующие преобразования полученной матрицы: если какие-либо два столбца матрицы Петри имеют одинаковое начало и конец, из более длинного столбца нужно вычесть более короткий, т.е. если 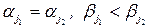 , то
, то 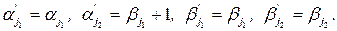 Если
Если 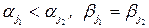 то
то 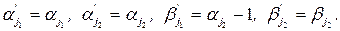 Если
Если 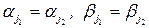 , то матрица Петри вырождена. При
, то матрица Петри вырождена. При 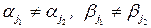 преобразования не производить. Таким образом, после каждого шага описанных преобразований получается опять матрица Петри. Эти действия нужно производить до тех пор, пока матрица Петри не станет единичной. На месте прежней единичной матрица будет стоять обратная матрица.
преобразования не производить. Таким образом, после каждого шага описанных преобразований получается опять матрица Петри. Эти действия нужно производить до тех пор, пока матрица Петри не станет единичной. На месте прежней единичной матрица будет стоять обратная матрица.
Для обоснования описанных преобразований необходимо показать, что в квадратной 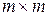 матрице Петри всегда существуют два столбца, у которых либо начала, либо концы совпадают. Предположим обратное: пусть ни начала, ни концы не совпадают ни для какой пары столбцов. Упорядочим столбцы по началам:
матрице Петри всегда существуют два столбца, у которых либо начала, либо концы совпадают. Предположим обратное: пусть ни начала, ни концы не совпадают ни для какой пары столбцов. Упорядочим столбцы по началам: 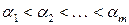 . Тогда
. Тогда 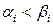 (
( 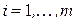 ). Имеем
). Имеем 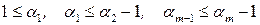 , сложив
, сложив 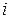 первых неравенств, получим
первых неравенств, получим 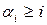 и, в частности,
и, в частности, 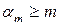 , что возможно лишь в случае
, что возможно лишь в случае 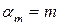 . Значит,
. Значит, 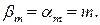 Рассмотрим
Рассмотрим 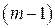 -й столбец. Так как
-й столбец. Так как 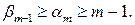 , это возможно в двух случаях: 1)
, это возможно в двух случаях: 1) 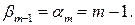 и 2)
и 2) 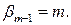 . Последний случай не подходит, так как
. Последний случай не подходит, так как 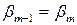 , а
, а 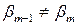 ‑ согласно предположению. Итак,
‑ согласно предположению. Итак, 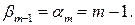 Рассуждая аналогично, можно показать, что
Рассуждая аналогично, можно показать, что 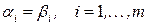 (единичная матрица). Во всех остальных случаях, когда матрица Петри – не единичная, можно либо привести ее к диагональному виду, либо матрица – вырожденная (если какие-либо два столбца имеют одинаковые начала и концы).
(единичная матрица). Во всех остальных случаях, когда матрица Петри – не единичная, можно либо привести ее к диагональному виду, либо матрица – вырожденная (если какие-либо два столбца имеют одинаковые начала и концы).
Можно показать, что унимодулярны также матрицы Петри при выполнении условий 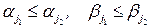 при
при 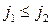 для столбцов и с дополнительными строками из единиц, имеющими «лестничную» структуру, пример которой приведен ниже:
для столбцов и с дополнительными строками из единиц, имеющими «лестничную» структуру, пример которой приведен ниже:
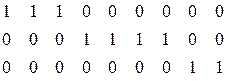
Если эти условия не выполняются, можно привести пример матрицы, которая не является унимодулярной. Так, матрица Петри с добавленной последней строкой из единиц
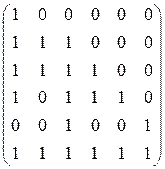
имеет определитель, равный 2, и, значит, не унимодулярна.
[1] Доказательство теоремы 3.1 приведено в [10].
[2] Щербина О.А. О задаче оптимизации предварительного резервирования гостиничных номеров // Исследование операций и АСУ. ‑ Киев: КГУ. 1976. ‑ Вып.7. ‑ С. 105-112.
[3] The Temporal Knapsack Problem and its solution / M. Bartlett [et al.] // Second International Conference on the Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems (CPAIOR, May 2005), pp. 34-48.
[4] Sulistio A. Advance Reservation and Revenue-based Resource Management for Grid Systems, Ph.D. Thesis, The University of Melbourne, Australia, 2008.
Дата добавления: 2016-06-05; просмотров: 1436;











