Задачи транспортного типа

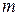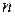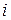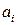Постановка задачи. Пусть имеется пунктов производства и пунктов потребления однородного продукта. Объем производства в пункте производства равен ; объем потребления в пункте потребления 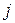равен 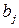(i = 1, 2,..., m; j = 1, 2,..., n).

Предполагается, что производство и потребление сбалансированы, т.е.

.

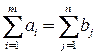Задана матрица 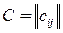транспортных расходов: затраты на перевозку единицы продукции из пункта производства 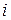в пункт потребления .

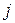Требуется составить план перевозок, который удовлетворяет ограничениям по мощностям производителей, полностью удовлетворяет спрос потребителей и минимизирует суммарные затраты на перевозки.

Через 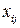обозначим объем перевозки из пункта производства 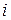в пункт потребления 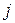, 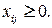Тогда известная из курса исследования операций транспортная задача имеет вид:

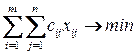
при ограничениях

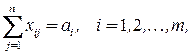
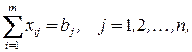
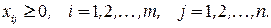
Транспортная задача ‑ это задача линейного программирования, число переменных которой равно 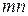, число ограничений равно 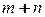. Ранг матрицы транспортной задачи не превосходит 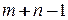. Известно, что условие сбалансированности производства и потребления является необходимым и достаточным условием разрешимости транспортной задачи.

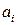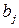Целочисленностъ базисных решений транспортной задачи. Если все значения и целочисленны, то все базисные решения транспортной задачи целочисленны. Из курса исследования операций известно, что можно построить начальное базисное целочисленное решение (с помощью метода минимального элемента или метода северо-западного угла). Далее, переход от одного базисного решения к другому в методе потенциалов не может нарушить целочисленности значений 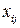, так как в процессе работы метода потенциалов выполняются лишь аддитивные операции (сложения и вычитания) над целочисленными значениями.

Целочисленность базисных решений транспортной задачи не связана с конкретным вычислительным алгоритмом, а является следствием теоремы 3.1.

Переформулируем эту теорему применительно к транспортной задаче.

Теорема 3.2. Каждая перевозка 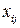любого базисного решения транспортной задачи является линейной комбинацией чисел 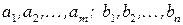с коэффициентами 0, .

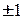Доказательство этой теоремы основано на следующей лемме.

Лемма. Любой минор матрицы условий транспортной задачи равен 0 или .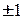

Другими словами, матрица условий транспортной задачи – унимодулярна.