Целочисленные многогранные множества.
Унимодулярные задачи целочисленного программирования.
Определение унимодулярной задачи целочисленного программирования.
Определение 3.1. Матрица А, все миноры которой равны либо 0, либо 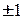 , называется унимодулярной матрицей.
, называется унимодулярной матрицей.
Целочисленные многогранные множества.
В этом параграфе рассматриваются целочисленные многогранные множества, т.е. многогранные множества, все вершины которых целочисленны. Важность изучения этих множеств обусловлена тем, что прямой симплекс-метод, как и другие конечные методы линейного программирования, определяет именно базисное оптимальное решение (если задача имеет решение). Поэтому если все базисные решения некоторой задачи линейного программирования целочисленны, то алгоритмы линейного программирования позволяют найти оптимальное (базисное) решение, удовлетворяющее и требованию целочисленности, и являющееся также оптимальным решением соответствующей задачи целочисленного линейного программирования.
Многогранное множество называется целочисленным, если все его вершины (соответствующие базисным решениям) целочисленны (т.е. все их компоненты — целые числа).
Рассмотрим многогранное множество 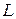 :
:
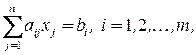
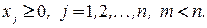
Справедлива следующая теорема.
Теорема 3.1.[1]Пусть 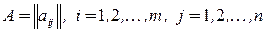 ‑ фиксированная матрица ранга
‑ фиксированная матрица ранга 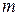 с целыми элементами. Для того чтобы многогранное множество
с целыми элементами. Для того чтобы многогранное множество 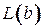 было целочисленным, необходимо и достаточно, чтобы любой минор порядка
было целочисленным, необходимо и достаточно, чтобы любой минор порядка 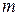 матрицы
матрицы 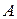 был равен либо 0, либо
был равен либо 0, либо 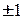 .
.
Дата добавления: 2016-06-05; просмотров: 2224;











