ЦИФРОВІЕ УСТРОЙСТВА. Основы алгебры логики.

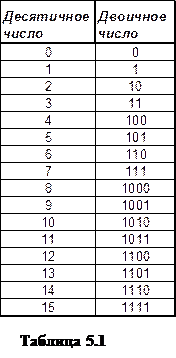В качестве математического аппарата для функций и аргументов, принимающих только два значения – 0 и 1, используется двоичная (булева) алгебра – алгебра логики.

Логическими (булевыми, двоичными) переменными (аргументами, высказываниями) в двоичной алгебре называются величины, которые независимо от их конкретной физической сущности могут принимать только два значения – 0 и 1.

Логические переменные, как и переменные обычной алгебры, обозначаются буквами латинского алфавита с различными индексами (например, х₀, х₁, х₂,…х_n). Индекс при переменной означает соответствующий разряд двоичного числа. Единичное значение переменной обозначается ее прямым индексом без отрицания. Так, если переменная х₁ = 1, то записывается она в коде двоичного числа как х₁. Если же х₁= 0, то соответственно записывается она с индексом отрицания, т.е. 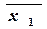. Поэтому двоичное _____ число 1001 может быть записано через переменные как х₃ х₂ х₁ х₀. Логической, булевой, или переключательной функцией (функцией двузначной алгебры логики) F(x₀,x₁,…,x_n) называют функцию, которая, как и ее n аргументов, может принимать лишь 2 значения –0 и 1. Таким образом, можно определить булеву функцию как двоичную функцию двоичного аргумента.

Булевы, или переключательные, функции бывают комбинационными и временными.

Комбинационными называются функции, значение которых однозначно определяется значениями их аргументов. Например, логическая функция совпадения равна единице только в том случае, когда все ее аргументы равны единице. В остальных случаях она равна нулю, причем это условие соблюдается независимо от порядка, последовательности и времени поступления аргументов.

Комбинационные функции иногда называют функциями без памяти, подчеркивая отсутствие в них свойства запоминания информации. Это означает, что после того, как изменение аргументов прекращается, тот факт, что они имели другое, чем в данный момент, значение уже не может влиять на формирование значения переключательной функции. Образно говоря, комбинационная функция «забывает» старые аргументы и может реагировать только на значения новых.

Схемы, реализующие комбинационные функции называются комбинационными (КС).

Временными называются функции, значения которых определяются как значениями аргументов в данный момент времени, так и другими параметрами, прежде всего временем, поэтому при одних и тех же значениях аргументов значения временной функции может быть разным.

Временные функции иногда называют функциями с памятью, определяя тем самым их важное качество- запоминание информации. Образно говоря, временные функции помнят либо предыдущее значение аргументов, либо предыдущее значение функции и реагируют как на новые значения аргументов, так и на прежние значения аргументов или функции.

Комбинационные функции и способы их задания.

Существуют различные способы задания или представления логических функций. Основными из них можно назвать следующие.

Словесное представление, отражающее словесную взаимосвязь ее аргументов со значениями функций (например, функция трех аргументов принимает значения единицы, если два или более ее аргументов равны единице), во всех других случаях функция равна нулю. Словесное представление логической функции предшествует любому другому способу представления, поскольку оно отражает неформальную взаимосвязь между аргументами и функцией.

Табличный способ, когда логическая функция задается в виде таблицы соответствия (таблицы истинности, состояний). При этом функция представляется в виде таблицы, в которой выписываются все возможные наборы аргументов в порядке возрастания их номеров, и для каждого набора устанавливается значение функции.

Число наборов аргументов, а значит, и число значений функции равно 2ⁿ, где ‑ n-число переменных.

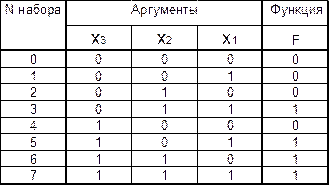В таблице 5.2 представлена функция, словесно заданная в предыдущем примере.

В булевой алгебре особое место занимают функции двух переменных. Имея набор функций двух переменных, на основании принципа суперпозиции можно образовать переключательную функцию любого числа переменных. Таблица 5.3

Так имеется 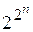различных 2ⁿ разрядных чисел, то количество переключательных функций от n-переменных конечно и равно .

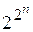Для n = 2 число различных переключательных функций равно 16. Эти функции называются элементарными и составляют максимальный набор элементарных логических функций. Все они представлены в таблице 1.3, в левой части которой приведены все четыре набора аргументов, а в правой 16 различных значений элементарных логических функций.

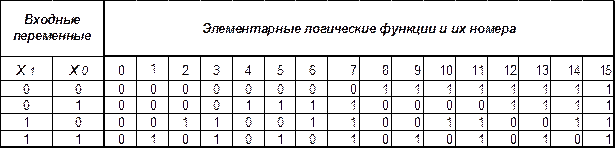Таблица 5.3

Каждая из этих элементарных логических функций имеет свое название (табл. 5.4). Приведенные функции неоднозначны по значимости, широте применения и технической реализации.

Наиболее широко используются функции И, ИЛИ, НЕ, ИЛИ-НЕ, И-НЕ. Они универсальны, с их помощью можно записать любую другую функцию, для них наиболее полно разработан математический аппарат.

Аналитический способ заданий функций заключается в том, что логическая функция F задается в виде алгебраического уравнения, в котором переменные хi связанны между собой знаками логических операций (табл. 3.4).

Существует две основные формы записи логических функций в алгебраическом виде, называемые нормальными.

Первая - дизъюнктивная нормальная форма (ДНФ)-представляет собой логическую сумму элементарных логических произведений (или дизъюнкцию элементарных конъюнкций), в каждое из которых аргумент или его отрицание входит не более одного раза.

Например,

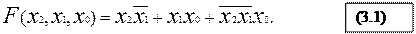Вторая форма, или конъюнктивная нормальная форма (КНФ), есть логическое произведение элементарных логических сумм (или конъюнкция элементарных дизъюнкций). Например,

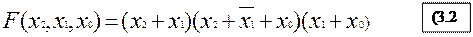
Аналитическая форма записи функций позволяет сформулировать основные законы (аксиомы) алгебры логики, которые записываются для операций И и ИЛИ отдельно.

Переместительные законы:

3.3 .

.

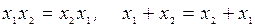Распределительный закон:

	3.4 .

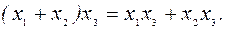
Таблица 5.4 Логические функции двух переменных

№ функц.	Название функции	Обозначение	Х1 – 0 1 0 1
Х2 – 0 0 1 1
Функция Y
	Константа нуль		0 0 0 0
	Конъюнкция, лог.умножение, И	Х1·Х2, Х1ÙХ2, Х1&Х2	0 0 0 1
2	Запрет по Х1, ЗАПРЕТ	Х1·Х2, Х1ÙХ2, Х1&Х2	0 0 1 0
	Переменная Х2	Х2	0 0 1 1
4	Запрет по Х2, ЗАПРЕТ	Х1·Х2, Х1ÙХ2, Х1&Х2	0 1 0 0
	Переменная Х1	Х1	0 1 0 1
	Неравнозначность, сумма по мод.2, исключающее ИЛИ	Х1ÅХ2, Х1+Х2(mod2)	0 1 1 0
	Дизъюнкция, логическое сложение, ИЛИ	Х1+Х2, Х1ÚХ2	0 1 1 1
8	Отриц. дизъюнкции, ф-ция Пирса, ИЛИ-НЕ	Х1+Х2, Х1ÚХ2	1 0 0 0
	Равнозначность, эквивалентность	Х1ºХ2	1 0 0 1
10	Отрицание Х1	Х1	1 0 1 0
	Импликация по Х1	Х1+Х2, Х1Х2	1 0 1 1
12	Отрицание Х2	Х2	1 1 0 0
	Импликация по Х2	Х1+Х2, Х1®Х2	1 1 0 1
14	Отрицание конъюнкции, функция Шеффера, И-НЕ	Х1·Х2, Х1ÙХ2, Х1&Х2	1 1 1 0
	Константа единица		1 1 1 1

Сочетательные законы:

3.5 .

( x₁x₃ ) x₃ = x₁ ( x₂x₃ );

( x₁+x₂ ) + x₃ = x₁ + (x₂+x₃ ).

Законы повторения:

3.6 .

xx = x

x + x = x.

Законы поглощения:

3.7 .

x₁ ( x₁ + x₂ ) = x₁;

x₁ + x₁x₂ = x₁.

Законы отрицания:

закон дополнительности

_

xx=0,

3.8

_

x+x=1;

правило де Моргана

___ _ _

3.9

x₁x₂= x₁+x₂,

____ _ _

x₁+x₂= x₁x₂;

закон двойного отрицания

3.10

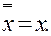
Законы склеивания:

3.11

3.12

Законы универсального множества:

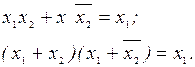
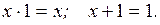
Законы нулевого множества:

	3.13

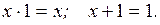
Доказательство истинности приведенных законов получают путем подстановки всех комбинаций переменных x_i (причем левая и правая части уравнений должны быть тождественны) или путем алгебраических преобразований на основе тех же законов.

Например, соотношение x₁ + x₁x₂ = x₁ может быть получено следующим образом:

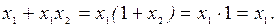
Числовой способ задания функций используется для сокращения ее записи, при этом переключательная функция записывается в виде логической суммы десятичных номеров двоичных наборов, на которых функция равна единице (в виде десятичных номеров конституент единицы), например, для функции, заданной табл. 1.2,

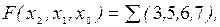
или

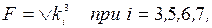
что читается как: функция F от трех переменных равна дизъюнкции конституент единицы 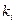, где i=3, 5, 6, 7.