Что такое Скин-эффект.

Существует несколько методов количесвтенной оценки степени ухудшения или улучшения призабойной зоны работающих (добывающих и нагнетательных) скважин. Наиболее предпочтительным является подход, согласно которому состояние призабойной зоны учитывается путем введения стационарного перепада давления, вызванному нестационарной фильтрацией в пласте. Это дополнительное падение давления, называемое «скин-эффектом», происходит в бесконечно тонкой зоне или «скин-зоне». Степень загрезнения определяется «скин-фактором» S, положительным при загрязнении и отрицательным в случае улучшения состояния призабойной зоны. Он может изменяться от -5 для скважин после проведения гидравлического разрыва пласта и до + 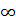для скважины, загрязненной настолько, что невозможно получить приток. Падение давления в скважине с улучшенной (или загрязненной) призабойной зоной отличается от падения давления в скважине с неизменной призабойной зоной на дополнительную величину:

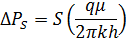
Рисунок 1а иллюстрирует идеализированный профиль давления для скважины с ухудшенной призабойной зоной (S>0). Поскольку толщину загрязненной зоны принимают бесконечно малой, то общее падения давления, вызванное скин-эффектом, происходит на стенке скважины. Представление скин-эффекта в виде тонкой области приводит к перемене знака градиента давления для скважины с улучшенной призабойной зоной (S<0), что показано на рисунке 1б. Хотя такое явление противоречит физике процесса фильтрации, все же понятие скин-фактора оказывается полезным для количественной оценки степени улучшения состояния призабойной зоны.

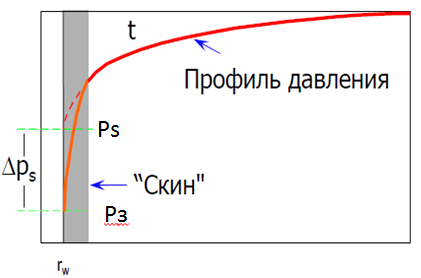
Рисунок 1а

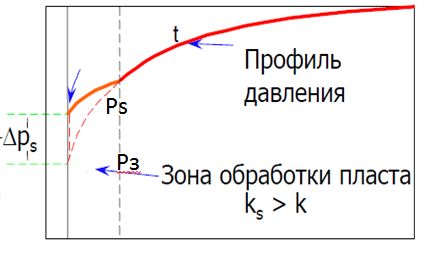
Рисунок 1б

Основная расчетная формула, используемая в ГДИС с учетом скин-фактора, представляется в виде:

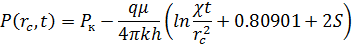
Тема №2. Влияние ствола скважины.

Наиболее распространенная техника и технологии снятия КПД-КВД предполагают замеры, регистрацию изменений забойных давлений (и дебитов) после пуска-закрытия скважины на устье с помощью предварительно спущенных на забой глубинных приборов и комплексов.

Используемые при ГДИС основные расчетные формулы - получены в предположении о мгновенном открытии-закрытии скважины (о мгно­венном пуске или прекращении притока через поверхность фильтрации на забое скважины). Так как обеспечить мгновенный пуск скважины с постоянным дебитом при снятии КПД достаточно сложно, то наиболее распространенным способом ГДИС на неустановившихся режимах является снятие КВД после остановки скважины, при этом обеспечи­вается условие: q=0=const. Однако это условие мгновенногозакрытия скважины при снятии КВД тоже сразу, мгновенно, не обеспечивается, так как между устьем скважины (устьевой задвижкой) и забоем имеется ствол скважины с объемом V. В работающей скважине перед ее закрытием ствол скважины заполнен полностью или частично газожидкостной смесью. После закрытия скважины на устье происходит изменение (рост) забойного давления во времени и пластовой флюид продолжает поступать в ствол скважины за счет сжатия газожидкостной смеси в стволе скважины

Дебит на забое - изменяется медленнее, чем на устье, где после закрытия задвижки q=0. Этот затухающий во времени после закрытия скважины на устье дебит часто называют после-эксплуатационным притоком, притоком-оттоком жидкости за счет сжатия флюидов в стволе скважины и других эффектов. После эксплуатационный приток искажает первоначальные участки кривых изменения забойного давления и обусловлен проявлением влияния объема ствола скважины (ВСС). Изменение термобарических условий в стволе скважины после закрытия на устье может вызывать сегрегацию фаз, фазовые превращения и др. процессы, которые влияют на монотонный характер затухания притока. В частности, при определенных условиях (при высоких газосодержаниях - газовом факторе и невысокой проницаемости ПЗП) возможен в некоторые промежутки времени отток жидкости из ствола скважины в пласт. Этот отток жидкости в пласт может снижать проницаемость ПЗП, и как следствие происходит уменьшение продуктивности скважины после каждой остановки скважины.

Эффект влияния ствола сопровождает не только остановку скважин, но и любую смену режима эксплуатации (пуск, изменение дебита и пр.). Количественной мерой эффекта влияния ствола является коэффициент влияния ствола скважины:

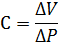
где 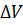– изменение объема флюида, приведенного к термобарическим условиям в стволе в начале притока, 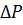– изменение давления.

Коэффициент послепритока может быть определен экспериментально. В частности, рассмотрим случай остановки скважины, работавшей до этого со стабильным расходом 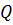. Если учесть, что дебит послепритока в момент остановки скважины равен дебиту до остановки, то можно предложить следующий способ определения дебита:

- проводится касательная к кривой изменения давления от времени в точке остановки скважины и определяется тангенс угла ее наклона – .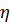

- рассчитывается коэффициент влияния ствола по формуле:

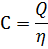
При исследовании с закрытием на устье необходимо проводить расчет времени ВСС и уже с учетом этого времени определять время регистрации КВД. Время ВСС рассчитывается по следующей методике:

1. Рассчитывался коэффициент ВСС по формуле:

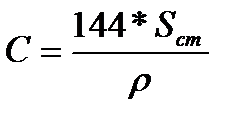, (1.7)

где: 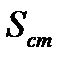- площадь поперечного сечения ствола скважины, в области, где происходит изменение уровня жидкости; 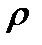- плотность жидкости;

2. Рассчитывается безразмерный коэффициент ВСС по формуле:

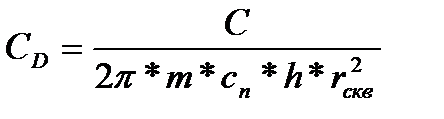, (1.8)

где: 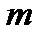- пористость; 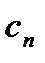- сжимаемость породы; 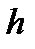- толщина пласта; 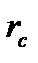- радиус скважины.

3. Рассчитывается безразмерное время окончание ВСС по формуле:

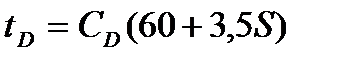, (1.9)

где: 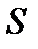- скин-фактор.

4. Рассчитывается время окончания ВСС в реальном исчислении по формуле:

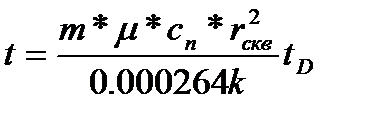, (1.10)

где: 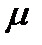- динамическая вязкость; 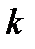- проницаемость.

Тема №3. Обработка КВД методами с учетом эффекта ВСС.

В некоторых случаях при исследовании скважины не удается получить прямоли­нейный участок кривой восстановления дав­ления в координатах 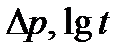. Чаще всего это объясняется существенным влиянием продолжающегося притока (или оттока) жидкости из пласта в скважину (или на­оборот) после ее закрытия на устье. В ука­занных случаях необходимо обрабатывав данные исследования с учетом притока жидкости в скважину после ее остановки.

Для обработки кривых восстановления давления с учетом притока жидкости не­обходимо одновременно с фиксацией изме­нения давления на забое регистрировать из­менение потока жидкости во времени либо измерять изменение давления на буфере и в затрубном пространстве во времени (для фонтанных и компрессорных скважин), а для насосных скважин определять измене­ние уровня жидкости в затрубном про­странстве.

Имеется несколько методов обработки кривых восстановления давления в скважи­не с учетом притока жидкости с целью определения параметров пластов и скважин. На основании исследований (сопоставление методов с помощью гипотетической кривой и по результатам исследований скважин высокоточными глубинными манометрами) большинство авторов рекомендуют при­менять при обработке кривых восстановле­ния давления два метода.

При замедленном притоке жидкости пред­почтительнее применять интегральный метод Э. Б. Чекалюка, а при высокой скорости за­тухания притока следует использовать диф­ференциальный метод Ю. П. Борисова. Ин­тегральный метод также применяют и в тех случаях, когда кривые восстановления давления имеют разброс точек.

Для учета ВСС существуют дифференциальные и интегральные методы.

1. Дифференциальный метод учета переменного притока после изменения режима работы скважины.

Суть метода заключается в исключении эффекта действия стоков, сопутствующих источникам, после изменения режима путем искусственной замены стоков источниками соответственно равных мощностей.

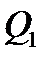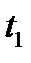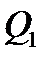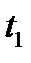Допустим скважина работала с дебитом , после чего в момент времени меняют режим на менее продуктивный. Если бы приток отсутствовал то вместо дебита мгновенно бы установился дебит . В действительности в момент времени (или несколько больший) скважина начинает работать с дебитом 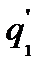, близким по величине к дебиту .

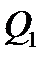Таким образом, в момент времени 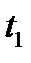мгновенно подключается источник 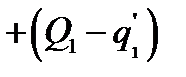значительно меньшей мощности, чем источник 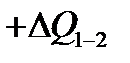. За время действии указанного источника 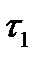глубинный манометр записывает начальный отрезок кривой восстановления, которую можно записать так:

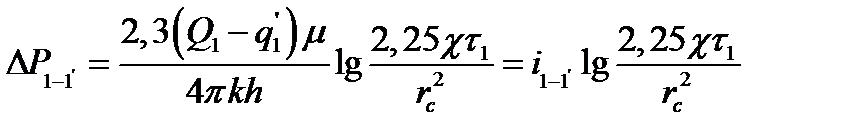, (1.42)

где: 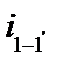- наклон начального отрезка кривой в координатах давление и логарифм времени.

В дальнейшем суммарная мощность подключающихся источников нарастает, соответствующая мощность «остающихся стоков» убывает. Наращивается кривая восстановления, уменьшается ее наклон в координатах давление и логарифм времени.

В определенный момент времени приток к забою прекращается и кривая восстановления выходит на свою асимптоту с угловым коэффициентом , который определяется из следующего соотношения:

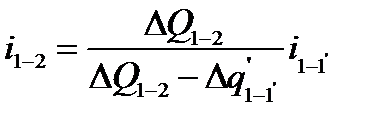, (1.43)

Применение описанного метода ускоренного вывода промысловой кривой восстановления на свою асимптоту позволяет использовать для обработки начальный участок кривой восстановления.

2. Дифференциальный метод учета переменного притока И.А.Чарного и И.Д.Умрихина.

Метод основан на решениях основного дифференциального уравнения, данных М.Маскетом и И.А.Чарным для притока упругой жидкости к кольцевому стоку с переменным во времени дебитом 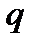, отсчитываемым от первоначального стационарного дебита 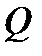. При замене кольцевого стока определенного радиуса равнодебитным точечным стоком радиуса, равного радиусу несовершенной скважины, основное соотношение этого метода представляется следующим образом:

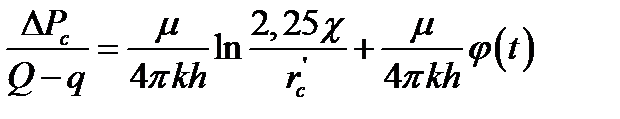, (1.44)

Если промысловую кривую восстановления строить в координатах 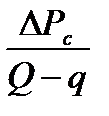и 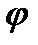, то получается прямая, по наклону которой 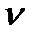и отрезку на оси ординат 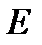можно определить параметры фильтрации:

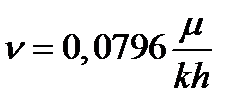, (1.45)

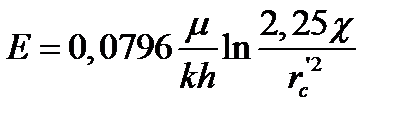, (1.46)

Интегральную функцию определяют по формуле:

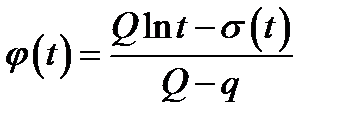, (1.47)

Интеграл 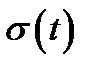находят по формуле:

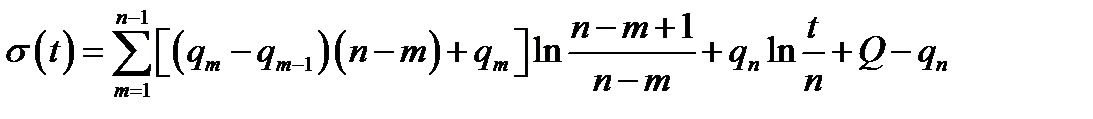, (1.48)

Весь период исследований 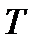делится на 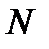равных промежутков. Интеграл 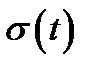находится для моментов времени 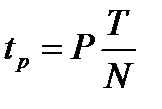, где 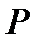меняется от единицы до .

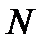3. Дифференциальный метод учета переменного притока Ю.П.Борисова.

Данный метод основан на решении М.Маскета для точечного стока в бесконечном пласте при переменном во времени дебите. При данном методе используется следующее уравнение:

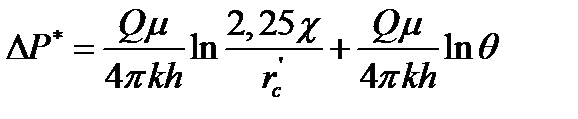, (1.49)

Промысловая кривая, будучи построена в координатах 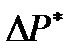и 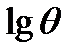, дает прямую с угловым коэффициентом:

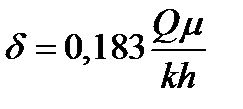, (1.50)

и отрезком на оси ординат:

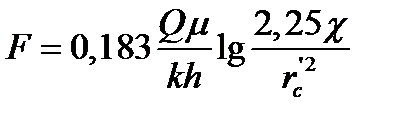, (1.51)

по которым находятся параметры пласта 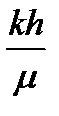и .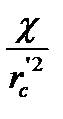

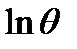учитывает дополнительный приток в зависимости от давления и площади затрубного пространства.

4. Интегральный метод учета переменного притока Г.И.Баренблатта, Ю.П.Борисова, С.Г.Каменецкого, А.П.Крылова.

Из всех рассмотренных методов этот метод является наиболее строго обоснованным математически и физически.

Метод основан на точном решении соответствующих обратных задач теории упругого режима и предусматривает вычисление интегралов от эмпирических функций, представляемой кривой восстановления давления.

В данном методе используется следующее основное соотношение:

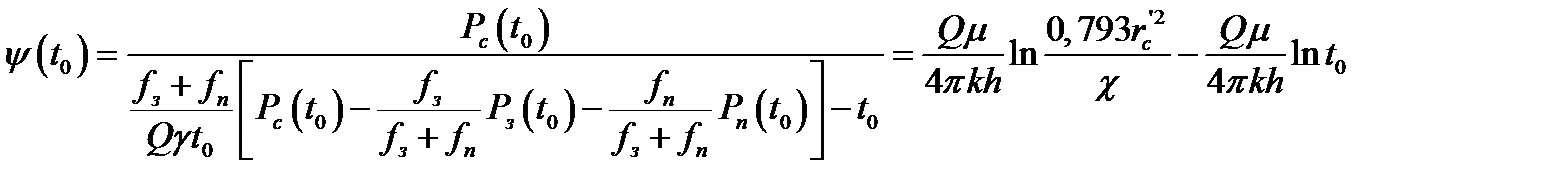, (1.52)

где: 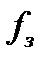и 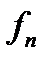- площадь сечения затрубного пространства и подъемных труб; 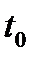- некоторая константа, имеющая размерность времен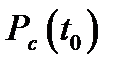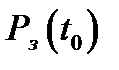и; , и 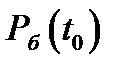- интегралы от соответствующих депрессий.

5. Интегральный метод Г.И.Баренблатта, и В.А.Максимова по определению некоторых неоднородностей пласта.

Данный метод является дальнейшим развитием главного интегрального метода. Рассматривается два случая: наличие вокруг забоя кольцевой загрязненной зоны и наличие на определенном расстоянии от скважины прямолинейного сброса. В зависимости от формы кривой построенной в координатах 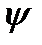и 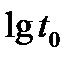возможно определить наличие одного из данных факторов.

6. Интегральный метод И.А.Чарного и И.Д.Умрихина.

В данном методе используется следующее основное соотношение:

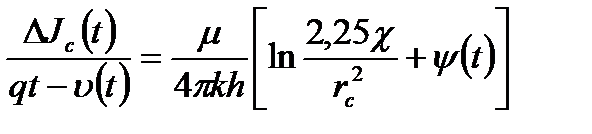, (1.53)

где

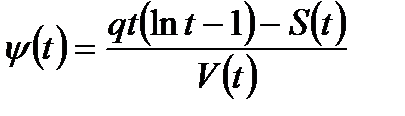, (1.54)

здесь

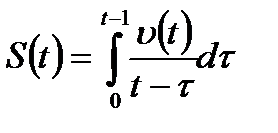, (1.55)

Графиком функции 1.53, преобразованной в координатах 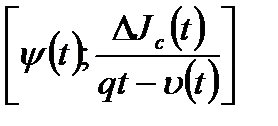, будет прямолинейный график с клоном 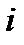и отрезком, отсекаемым его продолжение на оси ординат, по значениям которых определяются параметры 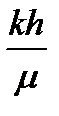и .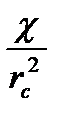

7. Интегральный метод Э.Б.Чекалюка.

Метод основан на использовании зависимости депрессии на забое скважины от суммарного объема притока упругой жидкости в виде интеграла Дюамеля:

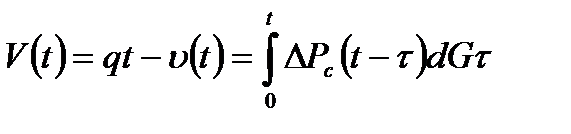, (1.56)

где 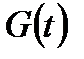- функция, определяющая объем добытой из пласта жидкости при постоянной депрессии, равной единице.

Основная расчетная формула интегрального данного метода имеет вид:

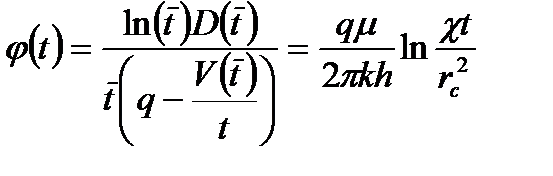, (1.57)

где 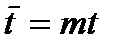- безразмерное время, 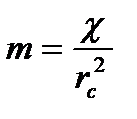- масштаб времени;

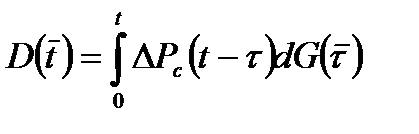, (1.58)

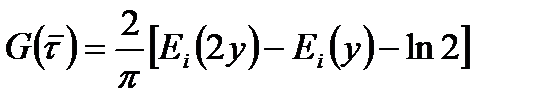
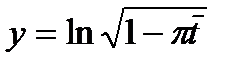
Графиком функции 1.57 в координатах 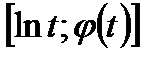будет прямолинейный график, по уклону и отрезку которых находят параметры пласта.

Большинство предложенных методов обработки КВД с учетом притока основываются на допущениях, что кривая 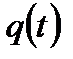имеет плавный монотонно убывающий «характер» зависящий от параметров пласта и пластовых флюидов. Однако на практике могут наблюдаться и немонотонные кривые, которые характеризуются наличием на кривой притока периодов времени, когда жидкость оттекает из ствола скважины в пласт после остановки на устье.

Тема №4. Обработка с помощью типовых кривых.

Типовые кривые – графическое представление давления как функции от времени для определенных конфигураций «скважина-пласт-граница». Они вычисляются на основе существующих аналитических моделей и выражаются в безразмерных переменных.

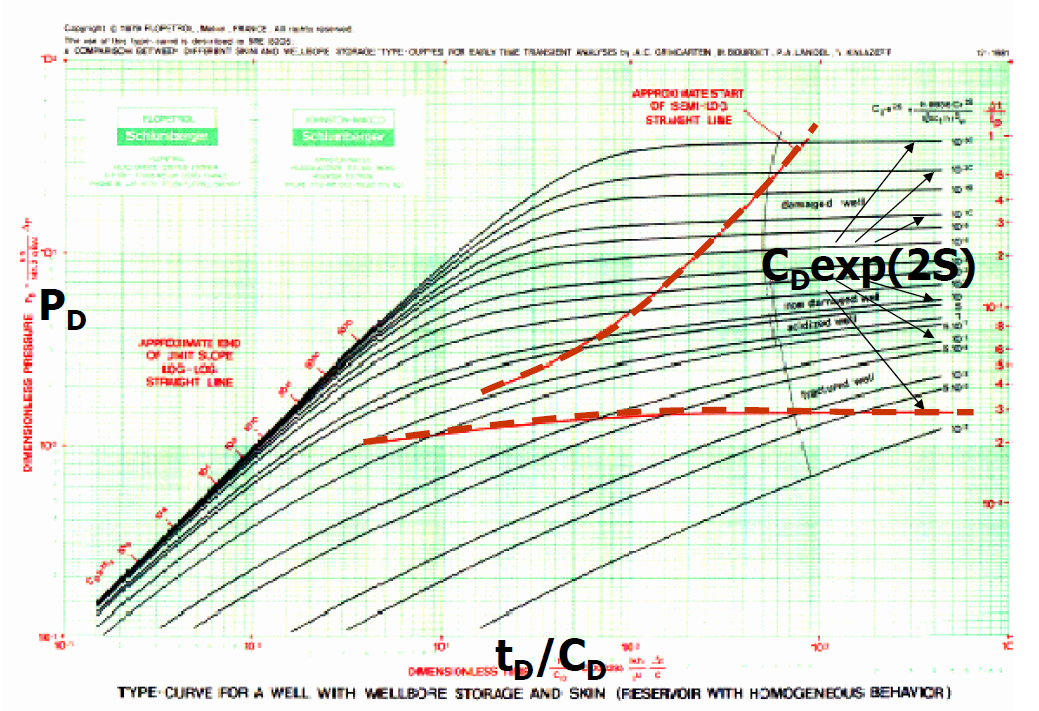
Универсальная кривая, построенная в билогарифмических координатах, наносится на прозрачную пленку (кальку) и накладывается на фактическую кривую - график прослеживания давления (также построенную в билогарифмических координатах, желательно с одинаковым масштабом бумаги в билогарифмических координатах) до возможно полного их совмещения, при обязательном соблюдении взаимной параллельности осей абсцисс и ординат фактического и универсального графиков. Это совпадение указывает на вероятность соответствия фактических данных модели (МПФС), для которой рассчитана данная (совпавшая) универсальная теоретическая кривая, вероятно, из-за неоднозначности решения обратных задач подземной гидродинамики.