Пересечение поверхностей с прямой
Универсальным способом определения точек пересечения прямой с поверхностью является способ вспомогательных секущих плоскостей, суть которого заключается в следующем: чтобы определить точки пересечения прямой с поверхностью, необходимо через прямую провести проецирующую плоскость, построить линию пересечения этой плоскости с поверхностью и отметить точки пересечения этой линии с прямой, которые и являются точками пересечения прямой с поверхностью.
П р и м е р 1. Построить точки пересечения поверхности вращения (тора) с прямой l (рис. 7.16).
Р е ш е н и е. Через проекцию прямой l2 проводим фронтально проецирующую плоскость Σ и строим на П1 проекцию линии пересечения этой плоскости с тором. Отмечаем точки пересечения этой линии с прямой l – М1 и N1. По принадлежности находим фронтальные проекции точек М2N2, определяем видимость этих точек и затем – всей прямой l.
Иногда рациональнее определять точки пересечения некоторых поверхностей с прямой с помощью преобразования комплексного чертежа.
П р и м е р 2. Построить пересечение сферы с прямой (рис. 7.17).
Р е ш е н и е. Через l1 проводим горизонтально проецирующую плос-
кость t. Плоскость пересекает сферу по окружности t1 с центром О. Параллельно плоскости окружности проводим ось П1/П4, из О1 – линию связи перпендикулярно П1/П4, определяем О4 и радиусом окружности проводим ее на П4. Строим проекцию и отмечаем точки М4 и N4, которые являются точками пересечения прямой со сферой. По принадлежности, с учетом видимости, определяем проекции точек М1, N1 и М2, N2.
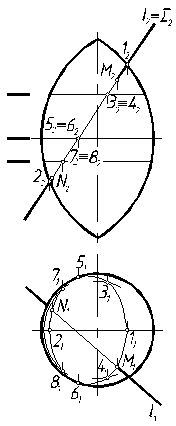
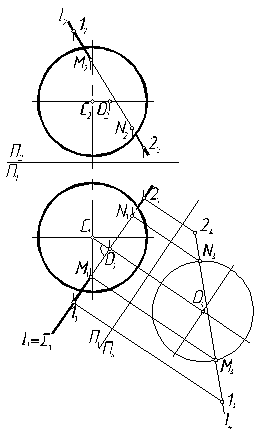
Рис. 7.16 Рис. 7.17
П р и м е р 3. Построить точки пересечения поверхности кругового цилиндра с прямой l (рис. 7.18).
Р е ш е н и е. Поверхность цилиндра можно представить в проецирующем положении, для чего достаточно заменить плоскость проекций П1 на П5. Построить проекции цилиндра и прямой, отметить точки М5 и N5, затем по принадлежности, с учетом видимости, – М2, N2, и М1, N1.
При построении точек пересечения прямой с эллиптическими цилиндрической или конической поверхностями целесообразно проводить вспомогательные плоскости через прямую параллельно образующим цилиндра или через вершину конуса соответственно. В этом случае плоскости пересекают эти поверхности по образующим; там, где эти образующие пересекают прямую, и находятся точки пересечения прямой с поверхностью. Образующие определятся при пересечении следа плоскости с основанием цилиндра (конуса).
П р и м е р 4. Определить точки пересечения прямой l с поверхностью наклонного эллиптического конуса (рис. 7.19).
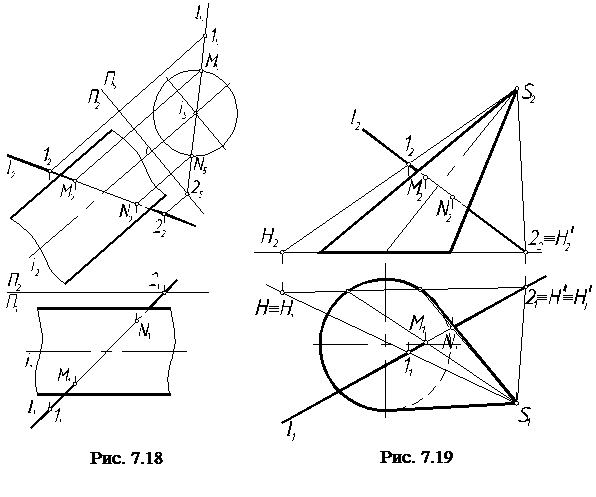
Р е ш е н и е. Через две произвольные точки прямой 1, 2 и вершину
конуса S проводим прямые. Определяем горизонтальный след полученной плоскости. Из точек пересечения следа плоскости и основания конуса проводим образующие. Отмечаем точки пересечения образующих и прямой – М1, N1 и М2, N2, которые и являются точками пересечения прямой l и конуса.
П р и м е р 5. Определить точки пересечения прямой l с поверхностью наклонного эллиптического цилиндра (рис.7.20).
Р е ш е н и е. Через две произвольные точки прямой 1, 2 проводим прямые параллельно образующим цилиндра. Определяем горизонтальный след полученной плоскости. Из точек пересечения горизонтального следа и основания цилиндра проводим образующие. Отмечаем точки пересечения образующих и прямой – М1, N1, M2, N2, которые и являются точками пересечения прямой l и цилиндра.
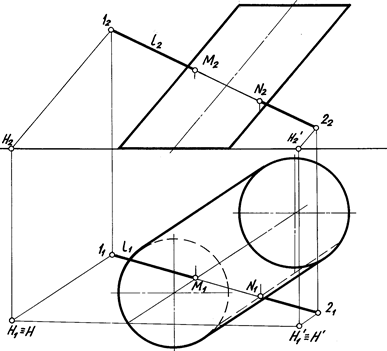
Рис. 7.20
Дата добавления: 2017-04-05; просмотров: 4368;











