Пересечение поверхностей плоскостью

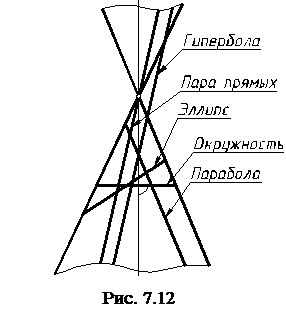Линия пересечения поверхности с плоскостью представляет собой плос-кую замкнутую линию, которая может быть плоской замкнутой ломаной прямой в случае пересечения многогранников. Линия определяется минимальным, но достаточным количеством точек, принадлежащих этой линии. Поверхность конуса вращения изображена на рис. 7.12. При различном наклоне секущей плоскости по отношению к оси конуса и образующим линия сечения представляет собой окружность, эллипс, гиперболу, параболу, пару прямых. При построении проекций эллипса достаточно иметь проекции точек, определяющие большую и малую оси. При построении параболы, гиперболы достаточно иметь проекции пяти точек, включая точки их вершин. При построении окружности необходимо знать ее центр и радиус. При построении линии пересечения многогранников необходимо определять точки пересечения ребер одного с гранями другого.

При определении линии пересечения поверхности плоскостью желательно иметь плоскость в проецирующем положении. С этой целью, при необходимости, выполняют преобразования комплексного чертежа. Тогда на одной из плоскостей проекции линия пересечения уже имеется, а на другой ее нужно определить из условия принадлежности точки поверхности. Это условие формулируется так: точка принадлежит поверхности, если принадлежит линии, лежащей в этой поверхности.

П р и м е р 1. Построить проекции сечения конуса вращения плоскостью Σ₂ (рис. 7.13).

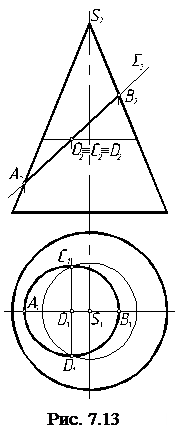Р е ш е н и е. Так как плоскость Σ является фронтально проецирующей и пересекает все образующие конуса, то в сечении получается эллипс.

На фронтальной плоскости проекций эллипс совпадает с Σ₂. Крайние точки А и В являются большой осью эллипса. На средине отрезка АВ находится малая ось эллипса СD. Решение задачи сводится к определению горизонтальных проекций точек А, В, С, D. Проекции А₁ и В₁ определены из условия, что эти точки принадлежат очерковым образующим конуса, их горизонтальные проекции совпадают с горизонтальной штрихпунктирной линией.

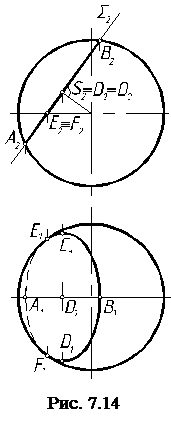Чтобы определить проекции точек С₁, D₁, через проекции точек C₂, D₂ проводим параллель, т. е. окружность, на которой лежат точки С, D. По большой и малой осям эллипса строится овал с помощью циркуля или лекала [5].

П р и м е р 2. Построить проекции линии сечения сферы проецирующей плоскостью Σ (рис. 7.14).

Р е ш е н и е. Так как плоскость фронтально проецирующая, то на П₂ линия сечения уже есть, она совпадает с Σ₂. Линия сечения представляет собой окружность, не параллельную П₂, поэтому проекция этой окружности на П₁ будет представлять собой эллипс. Чтобы построить этот эллипс, необходимы проекции точек большой и малой осей. Отрезок А₂В₂ является диаметром окружности в натуральную величину, т. е. фронталью, тогда А₁В₁ является малой осью эллипса. Проекции точек С₂D₂, лежащие на середине [А₂В₂], являются сопряженным диаметром фронтально проецирующего положения. Следовательно, С₁D₁ = [СD] = d_опр является большой осью эллипса. По большой и малой осям можно построить эллипс, но полезно предварительно построить точки смены видимости Е и F, которые лежат на экваторе. Линия эллипса слева от Е₁ и F₁ невидима, так как она находится под сферой.

П р и м е р 3. Построить проекции линии сечения поверхности конуса плоскостью общего положения (а h) (рис. 7.15).

Р е ш е н и е. Преобразуем плоскость общего положения в проецирующую способом замены плоскостей проекций. Для этого перпендикулярно горизонтали h₁ проводим координатную ось П₁/П₄ и на П₄ строим проекции плоскости и конуса, отмечаем большую ось А₄В₄ и малую С₄≡D₄. По принадлежности определяем проекции точек А₁, В₁, С₁, D₁, затем с условием видимости –
А₂, В₂, С₂, D₂.

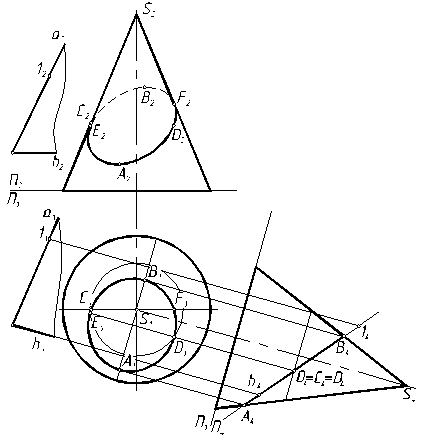
Рис. 7.15