Назначение коэффициентов смещения

Для нарезания зубчатых колёс

Коэффициенты смещения назначаются с целью:

– увеличения изгибной прочности зуба путём увеличения его опасного сечения вблизи основания;

– увеличения контактной прочности зуба путём использования участков эвольвенты, более удалённых от основной окружности;

– выравнивания максимальных удельных скольжений;

– предотвращения подреза малого колеса в передаче;

– увеличения плавности работы передачи путём удлинения активной линии зацепления;

– обеспечения заданного межосевого расстояния;

– обеспечения двухпарного зацепления в полюсе и других целей.

Расчёт геометрических размеров зубчатых колёс

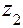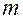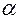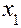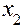Исходными данными для расчёта размеров служат: числа зубьев колёс и , модуль колёс , угол профиля исходного контура , коэффициенты смещения и , коэффициент высоты головки зуба 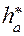и коэффициент радиального зазора .

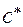Угол зацепления

Формулу для определения угла зацепления приведём здесь без вывода из-за его громоздкости

.

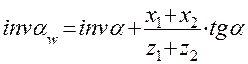Из этой формулы, в частности, видно, что в нулевой передаче 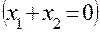угол зацепления равен углу профиля инструмента 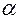, в положительной передаче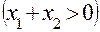 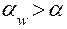, в отрицательной передаче всё наоборот, т.е. 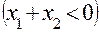и соответственно .

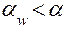Радиусы начальных окружностей и межосевое расстояние

Для вывода формул обратимся к рис. 3.17, на котором показаны необходимые элементы зацепления. Линия зацепления N₁N₂ образует угол зацепления α_w с общей касательной к начальным окружностям радиусов 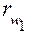и 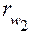, касающимся друг друга в полюсе Π. Опустив перпендикуляры из центров колёс O₁ и O₂ на линию зацепления, получаем два прямоугольных треугольника N₁O₁П и N₂O₂П с углами при вершинах O₁ и O₂, равными α_w. Из треугольника следует N₁O₁П , из треугольника N₂O₂П– 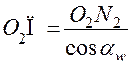. Так как имеют место равенства 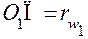, , 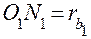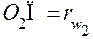и 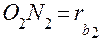, а также 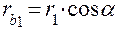, , 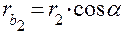то получаем 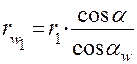и 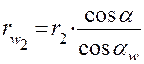. Вместо радиусов делительных окружносте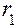й и 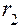в эти формулы можно вставить их выражения, записанные ранее, тогда

, .

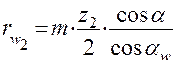Как видно из рисунка, межосевое расстояние равно сумме радиусов начальных окружностей, т. е. 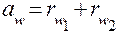, поэтому

.

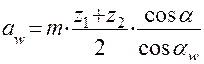Произведение первых двух слагаемых в этой формуле называется делительным межосевым расстоянием. Оно имеет место, когда передача изготавливается нулевой, т. е. когда суммарный коэффициент смещения равен нулю. При этом 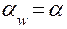, и косинусы сокращаются.