Метод неопределённых коэффициентов.
Предназначен для получения линейных форм логических формул, может быть применен для минимизации логических формул для любого числа переменных. В ручном варианте применяют для числа переменных не более пяти. Логическую функцию представляют в виде ДНФ. В общем виде, например, для трех переменных она имеет следующий вид:
f(x1,x2,x3) = k11x1Ú k01x1Ú k12x2Ú k02x2Ú k13x3Ú k03x3Ú k1112x1x2Ú k1012x1x2Ú k12x1x2Ú k0112x1x2 Ú k0012x1x2 k1113x1x3Ú k1013x1x3Ú k0013x1x3 Ú k1123x2x3 Ú k1023x2x3Ú k0123x2x3Ú k0023x2x3Ú k111123x1x2x3Ú k110123x1x2x3Ú k101123x1x2x3Ú k100123x1x2x3Ú k011123x1x2x3Ú k010123x1x2x3Ú k001123x1x2x3Ú k000123x1x2x3
В этой дизъюнктивной норм. форме коэффициенты с индексами – это определенный коэффициент, принимающий значение 0 и 1 и подбирается таким образом, чтобы ДНФ была минимальная. Задавая различные наборы переменных x1,x2,x3 и приравнивая полученные выражения соответствующим значениям функции, получают систему уравнений для определения коэффициента к:
f(0,0,0) = k01Ú k02 Ú k03Ú k0012Ú k0023Ú k000123
f(0,0,1) = k01Ú k02 Ú k13Ú k0012Ú k0113Ú k0123Ú k001123
……………………………………………
f(1,1,1) = k11Ú k12 Ú k13Ú k1112Ú k1113Ú k1123Ú k111123
f(x1,x2,x3) = 0 Ú 1
Задание некоторой функции определяет значение первых частей системы: если f = 0 на соответствующем наборе переменных, то все коэффициенты входящие в уравнение, будут равны нулю. Это следует из свойства дизъюнкции. Тогда и в уравнении, где функция принимает единичное значение, надо вычеркивать все нулевые коэффициенты. Из оставшихся коэффициентов надо выбрать такой, который определяет темп наименьшего, и приравнять его к единице. А остальные коэффициенты приравнять к 0. Т.о. единичные коэффициенты определяют искомую ДНФ для системы уравнений.
Рассмотрим f(x1,x2,x3) = Ú F(0,2,4,7), так называется десятичная форма записи для логического выражения f(x1,x2,x3)= ,, Ú , x2, Ú x1,, Ú x1, x2, x3
Для получения коэффициентов: 1) Выбрать строку, в которой функция равна нулю, и все коэффициенты приравнять к нулю. Если все нулевые строки просмотрены, то переходим к шагу 2. 2) Просмотрим строки, где функция равна еденице, и в этих строках вычеркиваем коэффициенты, которые принадлежат строкам с нулевым значением функции. 3)Переписывают все модифицированные уровнения.
В полученной системе уравнений просматривают каждую строку и вычеркивают максимально возможное количество коэффициентов таким образом, чтобы ранг оставшихся терминов был минимальным.
k0023Ú k0013Ú k000123=1
k0013Ú k000123=1
k0023Ú k000123=1
k000123=1
В модифицированной системе вычеркивают коэффициенты максимального ранга. Оставшиеся коэффициенты позволяют получить минимальную форму:
f*(x1,x2,x3)= ,Ú , Ú x1,x2,x3
Метод карт Карно
Метод Карно основан на законе склеивания. Склеиваются наборы , отличающиеся друг от друга значением одного разряда. Такие наборы называются соседними. Карно закодировал клетки своей карты так ,что в соседних клетках оказались соседние, а значит, склеивающиеся наборы. Соседними могут быть не только отдельные клетки, которые мы назовем элементарными квадратами Карно, но и целые группы соседних клеток(назовем их прямоугольниками Карно). Под прямоугольником Карно[13] будем понимать некоторую, зачастую разрозненную фигуру покрытия, все соседние клетки которой закодированы соседними наборами. Например, на вышеприведённом рисунке в поле карты для 4-х переменных изображён прямоугольник Карно P, состоящий из четырёх элементарных квадратов Карно, описываемых наборами x4'x3'x2'x1' , x4'x3'x2x1' , x4x3'x2'x1' , x4x3'x2x1' . Если над логической суммой этих четырёх наборов произвести последовательно операции склеивания, то мы аналитически получим результат в виде импликанты (под импликантой будем понимать неполный набор)x3'x1'. Карта Карно позволяет получить этот результат графически значительно быстрее и проще. Для решения этой задачи используем алгоритм графической минимизации.Кстати говоря,сам Карно никакого алгоритма не предложил.
Правило склеивания. Карты Карно
Упрощение выражений булевых функций (минимизация) основывается на понятии несущественности переменных. Переменная называется несущественной на паре наборов, если при изменении ее значения на противоположное булева функция сохраняет свое значение.
Например, для булевой функции трех переменных, f (1,3,5,6,7)=1 , которая рассматривалась в подразделе 1.3 "Теории переключательных схем", 6-я и 7-я конъюнкции имеют вид : x1x23, x1x2x3. По дистрибутивному закону :
x1x23 v x1x2x3 = x1x2 ( 3 v x3 ) = x1x2.
Таким образом, две конъюнкции, содержащие несущественную переменную, заменяются одной, в которой несущественная переменная отсутствует.
В кубическом виде склеивание имеет следующую интерпретацию : 1 1 0 1 1 1 = 1 1 X , что соответствует конъюнкции x1x2.
Приведем основные определения, используемые при минимизации булевых функций. Данные определения используют понятия нормальных (канонических) форм булевых функций, введенные в подразделе 1.3 .
Число переменных, входящих в элементарную конъюнкцию (для ДНФ) или в элементарную дизъюнкцию (для КНФ) называется ее рангом.
В основе любых методов минимизации лежит операция склеивания. Два элементарных произведения одного ранга (для ДНФ) или элементарных сумм одного ранга (для КНФ) склеиваются, если они различаются только по одной переменной.
Операция Аx v A = A называется полным склеиванием, а операция Аx v A = A v Аx v A - неполным склеиванием (для ДНФ).
Операция ( А v x )· ( A v ) = A называется полным склеиванием, а операция ( А v x )· ( A v ) = A· ( А v x )· ( A v ) - неполным склеиванием (для КНФ).
Например, полное склеивание (x1 v x2 v x3)· (x1 v x2 v 3) = x1 v x2 ;
Неполное склеивание x1x2x3 v x1x23 = x1x2 v x1x2x3 v x1x23 .
Импликантой называется элементарное произведение, равное 1 на одном или нескольких наборах, где данная функция равна 1, и равное 0 на всех наборах, где данная функция равна 0. Импликанта покрывает один или несколько минтермов рассматриваемой булевой функции. Обычно, импликанта - это результат склеивания соответствующих минтермов или импликант.
Простая импликанта - это импликанта, которая содержит хотя бы минтерм функции, но перестает быть импликантой после удаления любого аргумента (иными словами, это импликанта, к которой не нельзя применить операцию склеивания).
Сокращенная ДНФ - это дизъюнкция всех простых импликант.
Существенная импликанта - это простая импликанта, образованная склеиванием таких минтермов, что по крайней мере для одного из них эта операция была единственной. Существенные импликанты образуют ядро функции.
Тупиковая ДНФ - это дизъюнкция простых импликант, из которых ни одна не является лишней.
МДНФ (минимальная ДНФ) - тупиковая ДНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.
Имплицентой называется элементарная логическая сумма, равная 0 на одном или нескольких наборах, где данная функция равна 0, и равная 1 на всех наборах, где данная функция равна 1. Имплицента покрывает один или несколько макстермов рассматриваемой булевой функции. Обычно, имплицента - это результат склеивания соответствующих макстермов.
Простая имплицента - это имплицента, которая содержит хотя бы макстерм функции, но перестает быть имплицентой после удаления любого аргумента (иными словами, это имплицента, к которой не нельзя применить операцию склеивания).
Сокращенная КНФ - это конъюнкция всех простых имплицент.
Существенная имплицента - это простая имплицента, образованная склеиванием таких макстермов, что по крайней мере для одного из них эта операция была единственной. Существенные имплиценты образуют ядро функции.
Тупиковая КНФ - это конъюнкция простых имплицент, из которых ни одна не является лишней.
МКНФ (минимальная КНФ) - тупиковая КНФ с минимальным числом вхождений переменных (минимальным числом букв) по сравнению с другими тупиковыми формами этой функции.
Правила минимизации с использованием карт Карно
1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.
2. Количество клеток внути контура должно быть целой степенью двойки (1, 2, 4, 8, 16...).
3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).
4. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.
5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.
6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ). Целью минимизации является нахождение минимальной из множества тупиковых форм.
7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0. Для значений булевой функции, равных 0, записываются элементарные дизьюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1.
Если рассматривать запись результатов минимизации в кубическом виде, то при минимизации булевой функции по единичным значениям, каждой конъюнкции ранга R соответствует куб ранга R, где каждой переменной без инверсии соответствует 1 в кубе, переменной с инверсией - 0, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует единичное покрытие C1 (соответствующее ДНФ).
При минимизации булевой функции по нулевым значениям и представлении результатов минимизации в кубическом виде, нулевое покрытие C0 формируется на основе обратной ДНФ , которая является инверсной функцией по отношению к КНФ (способ построения инверсных функций и пример инверсных функций для f ( 1,3,5,6,7 ) = 1 рассмотрен в подразделе 1.3). Отметим, что обратная ДНФ строится на основе КНФ. Таким образом каждой дизъюнкции ранга R (из КНФ) соответствует куб ранга R, где каждой переменной без инверсии соответствует 0 в кубе, переменной с инверсией - 1, а на месте отсутствующей переменной ставиться X . Полученное множество кубов образует нулевое покрытие C0.

При данном способе задания таблица истинности функции представляется в виде координатной карты состояний, которая содержит 2n клеток (по числу входных наборов булевой функции n переменных). Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца карты, а другая - координаты строки.
При такoм способе построения каждая клетка определяется значениями переменных, соответствующих определенному двоичному набору. Внутри каждой клетки карты Карно ставится значение функции на данном наборе. Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е. были соседними. Поэтому значения переменных в столбцах и в строках карты образуют соседний код Грея. Такой способ представления очень удобен для наглядности при минимизации булевых функций.
Карты Карно были изобретены в 1952 Эдвардом В. Вейч’ем и усовершенствованы в 1953 Морисом Карно, физиком из "Бэлл Лабс"Метод карт Карно применим к минимизации булевых функций до 6-ти переменных (до 4 переменных на плоскости) и до 6 - в трехмерной интерпретации.
Если требуется получить карту Карно для какой – либо функции, сначала надо записать эту функцию в СДНФ, – в совершенной дизъюнктивно нормальной форме, или в виде таблицы истинности.
Каждое слагаемое булева выражения в СДНФ, или каждая единица в столбце функции таблицы истинности, задается на карте Карно единицей в соответствующей клетке. Координаты этой клетки содержат те же входные переменные и их инверсии, что и данное слагаемое СДНФ булева выражения ( или данная строка таблицы истинности ).
Taблица истинности для четырех переменных включает 16 строк, следовательно карта Карно должна состоять из 16 клеток, как показано на рисунке:
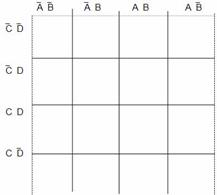
У карты Карно для четырех переменных клетки крайнего левого столбца должны рассматриваться как соседние для клеток крайнего правого столбца, а клетки верхней строки, – как соседние для клеток нижней строки. Другими словами можно сказать, что эта карта расположена на поверхности цилиндра (склеили правый край карты с левым ), изогнутого и растянутого так, что его верхний срез соединяется с нижним срезом; при этом цилиндр превращается в тор (бублик).
Правила упрощения заполненной карты Карно для четырех переменных заключаются в следующем :
– соседние две, четыре, или восемь единиц обводят общим контуром;
– контур должен быть прямоугольным без изгибов или наклонов;
– каждый контур превращает все входящие в него единицы в одну, т.е. объединенные таким образом слагаемые СДНФ булева выражения дают одно слагаемое в упрощенном выражении;
– те входные переменные, которые входят в координаты данного контура совместно со своими инверсиями, исключаются из слагаемого, которое дает этот контур в упрощенное выражение.
Примеры упрощения булевых выражений с помощью карты Карно:
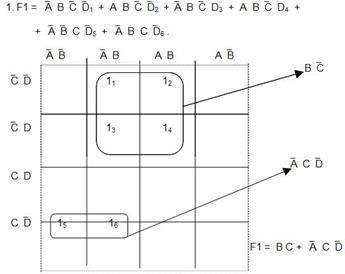
В первом примере минимизации булевой функции F1 нижний контур из двух единиц 15 и 16 , соответствующие пятому и шестому слагаемым в исходном булевом выражении, дает возможность опустить B и`B. После этого в нем остается произведение `A C`D. В верхнем контуре из четырех единиц 11, 12, 13 и 14 , соответствующие первым четырем слагаемым в исходном булевом выражении попарно опускаются A и`A, D и`D, так что в результате этого верхний контур дает произведение B C.
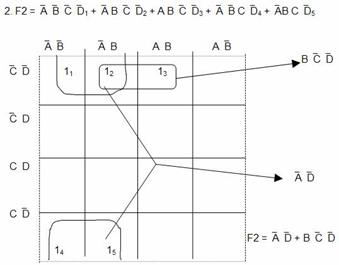
Во втором примере минимизации булевой функции F2 контур из двух единиц 12 и 13 , соответствующие второму и третьему слагаемым в исходном булевом выражении, дает возможность опустить А и`А. После этого в нем остается произведение B`C`D. В контуре из четырех единиц 11, 12, 14 и 15 , соответствующие другим четырем слагаемым из исходного булева выражения, попарно опускаются В и`В, С и`С, так что в результате этого верхний контур дает произведение `A`D.
Карта Карно представляется в данном случае свернутой в цилиндр, в котором верхний край совмещается с нижним. Этот пример показывает также, что контура могут накладываться друг на друга.
Правило покрытия 1.
Любой области из 2k смежных клеток можно поставить в соответствие конъюнкцию (n-k)-го ранга, состоящую из переменных, которые имеют постоянное значение во всех единичных наборах, соответствующих клеткам области. Причем переменная xi включается в конъюнкции в прямом виде, если эта переменная имеет значение 1 на всех клетках области. Соответственно переменная xi включается в конъюнкции в инверсном виде, если она имеет значение 0 на всех клетках области. "Покрытая" область на карте обводится контуром. Дизъюнкция конъюнкции, совместно покрывающих все клетки карты, заполненные единицами, есть одна из ДНФ переключательной функции.
Цель минимизации формулы ПФ по карте Карно - "покрыть" все клетки, содержащие единицы, наименьшим числом конъюнкции наименьшего ранга, т. е. "покрыть" наименьшим числом контуров, каждый из которых охватывает как можно большую область смежных клеток, все клетки, содержащие единицы. Дизъюнкция полученных конъюнкций есть одна из тупиковых (возможно, минимальная) ДНФ функции.
Простым импликантам (минималям) в методе Квайна-Мак-Класки на карте Карно соответствуют области смежных клеток, не являющиеся частью никакой другой области смежных клеток.
Обязательной простой импликанте (экстремали) в методе Квайна-Мак-Класки соответствует область смежных клеток, которая покрывает хотя бы одну единичную клетку, не входящую в состав никакой из других областей смежных клеток.
Правило покрытия 2.
Любой смежной области 2k клеток, заполненных нулями, можно поставить в соответствие дизъюнкцию (n-k)-го ранга, состоящую из переменных, которые имеют постоянное значение во всех нулевых наборах, соответствующих клеткам области, причем переменная xi входит в дизъюнкцию в прямом виде, если имеет значение 0 на всех клетках области, и, соответственно в инверсном виде, если она имеет значение 1 на всех клетках области. Конъюнкция минимального числа дизъюнкций, совместно покрывающих все клетки карты, заполненные нулями, есть одна из тупиковых (возможно, минимальных) КНФ переключательной функции.
Метод Петрика
Метод Петрика используется для нахождения всех минимальных покрытий конституент единицы и позволяет получить все тупиковые ДНФ по импликантной матрице. Суть метода заключается в следующем. По импликантной матрице строится так называемое конъюнктивное представление импликантной матрицы. Для этого все простые импликанты обозначаются разными буквами (обычно прописными латинскими). После этого, для каждого i-ro столбца импликантной матрицы строится дизъюнкция всех букв, обозначающих строки матрицы, пересечение которых с i-м столбцом отмечено крестиком. Конъюнктивное представление импликантной матрицы образуется как конъюнкция построенных дизъюнкций для всех столбцов матрицы. К конъюнктивному представлению матрицы могут быть применены все соотношения булевой алгебры с целью его упрощения. После раскрытия скобок и выполнения всех возможных поглощений получается дизъюнкция конъюнкций, каждая из которых содержит все импликанты тупиковой ДНФ.
Рассмотрим табл. 3, строки которой соответствуют простым импликантам функции f, а столбцы — конъюнкциям совершенной ДНФ (СДНФ). В каждую клетку записываем единицу, если соответствующая простая импликанта поглощает элементарную конъюнкцию и нуль — в противном случае. Такая таблица называется «импликантной таблицей».
Согласно определению, каждая тупиковая ДНФ определяется таким набором строк, что в таблице, образованной этими строками в каждом столбце имеется одна единица, причём из этого набора нельзя удалить ни одной строки так, чтобы при этом ни один столбец не стал нулевым.
Таблица 3
| СДНФ Сокр. ДНФ | |||||||||
| P1 | 1__0 | ||||||||
| P2 | 101_ | ||||||||
| P3 | _001 | ||||||||
| P4 | 0_11 | ||||||||
| P5 | 01_1 |
Пусть в общем случае в таблице имеется N столбцов и m строк. Поставим в соответствие простым импликантам сокращённой ДНФ переменные P1 … Pm. Фиксируем некоторую дизъюнкцию простых импликант. Будем считать, что Pi = 1, если i-я простая импликанта входит в эту дизъюнкцию и Pi = 0, в противном случае. Запишем в виде формалы условие того, что рассматриваемая дизъюнкция является ДНФ функции. Для этого необходимо, чтобы в каждом столбце таблицы была хотя бы одна единица, т.е.
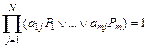 ,
,
где  — элемент матрицы (таблицы), стоящий в i-й строке и j-м столбце,
— элемент матрицы (таблицы), стоящий в i-й строке и j-м столбце, 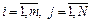 .
.
Эту формулу можно трактовать как КНФ некоторой двоичной функции от переменных P1 … Pm, которая принимает значение 1 только на тех наборах переменных, которые соответствуют некоторым ДНФ исходной функции, и значение 0 — на наборах, которые соответствуют наборам импликант, не являющихся ДНФ исходной функции.
Заметим, что функция 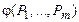 монотонна, так как формула 3 не содержит переменных с отрицаниями. Поэтому согласно утверждению 3 для нахождения её сокращённой ДНФ достаточно раскрыть скобки в формуле 3, а затем произвести все поглощения. Наконец, остаётся заметить, что в силу указанного выше свойства этой функции, её простые импликанты и только они будут давать тупиковые ДНФ исходной функции f.
монотонна, так как формула 3 не содержит переменных с отрицаниями. Поэтому согласно утверждению 3 для нахождения её сокращённой ДНФ достаточно раскрыть скобки в формуле 3, а затем произвести все поглощения. Наконец, остаётся заметить, что в силу указанного выше свойства этой функции, её простые импликанты и только они будут давать тупиковые ДНФ исходной функции f.
Для табл. 3 функция 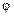 равна:
равна:
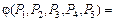
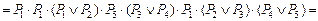
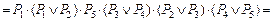
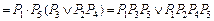 .
.
Отсюда P1P3P5 даёт для f тупиковую форму:
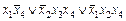 ,
,
а P1P2P4P5 даёт:
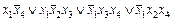 .
.
Метод Петрика используется для нахождения всех минимальных покрытий конституент единицы и позволяет получить все тупиковые ДНФ по импликантной матрице. Суть метода заключается в следующем. По импликантной матрице строится так называемое конъюнктивное представление импликантной матрицы. Для этого все простые импликанты обозначаются разными буквами (обычно прописными латинскими). После этого, для каждого i-ro столбца импликантной матрицы строится дизъюнкция всех букв, обозначающих строки матрицы, пересечение которых с i-м столбцом отмечено крестиком. Конъюнктивное представление импликантной матрицы образуется как конъюнкция построенных дизъюнкций для всех столбцов матрицы. К конъюнктивному представлению матрицы могут быть применены все соотношения булевой алгебры с целью его упрощения. После раскрытия скобок и выполнения всех возможных поглощений получается дизъюнкция конъюнкций, каждая из которых содержит все импликанты тупиковой ДНФ.
Пример.
Задана импликантная матрица (табл. 4.6.1). Найти методом Петрика все тупиковые ДНФ булевой функции f, описываемой данной матрицей.
| Таблица 4 | ||||||||
| Конституенты единицы | ||||||||
| Простые импликанты | /x1/x2/x3x4 | /x1/x2x3x4 | /x1x2/x3x4 | /x1x2x3x4 | x1x2x3/x4 | x1x2x3x4 | ||
| /x1x4 | Х | Х | Х | Х | ||||
| x2x3x4 | Х | Х | ||||||
| x1x2x3 | Х | Х | ||||||
Имеющиеся простые импликанты обозначим буквами:
/x1x4 = A. x2x3x4 = B. x1x2x3 = C.
Тогда конъюнктивное представление w матрицы имеет вид
w = A*A*A*(A v B)*C(B v C).
Упростим его.
w = A*(A v B)*C(B v C) = AC.
Тупиковая ДНФ содержит две простые импликанты: А = /x1x4 и C = x1x2x3 и имеем вид f = /x1x4 v x1x2x3."
Тема 21. Пять классов переключательных функций: линейные переключательные функции; переключательные функции, сохраняющие нуль; переключательные функции, сохраняющие единицу; монотонные переключательные функции; самодвойственные переключательные функции. Теорема о функциональной полноте. Основная функционально полная система логических функций. Функционально полные системы логических функций. Примеры функционально полных базисов.
Конечное множество булевых функций 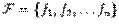 называют системой булевых функций. Систему булевых функций называют полной, если любая булева функция может быть выражена в виде формулы над этой системой (другими словами, если она представима через функции данной системы).
называют системой булевых функций. Систему булевых функций называют полной, если любая булева функция может быть выражена в виде формулы над этой системой (другими словами, если она представима через функции данной системы).
Примером полной системы является так называемый стандартный базис, содержащий дизъюнкцию, коньюнкцию и отрицание: 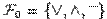 . Полнота этой системы легко доказывается тем, что любая булева функция может быть представлена в виде ДНФ или КНФ. А учитывая, что
. Полнота этой системы легко доказывается тем, что любая булева функция может быть представлена в виде ДНФ или КНФ. А учитывая, что 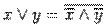 и
и  , полными являются даже системы
, полными являются даже системы 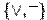 и
и  .
.
Другой распространённой полной системой булевых функций является базис Жегалкина: 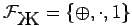 , включающий исключающее или, коньюнкцию и константу 1. Можно доказать, что любая булева функция представима в виде так называемого полинома Жегалкина:
, включающий исключающее или, коньюнкцию и константу 1. Можно доказать, что любая булева функция представима в виде так называемого полинома Жегалкина:

где 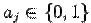 . В частном случае, полином Жегалкина имеет линейный вид:
. В частном случае, полином Жегалкина имеет линейный вид:

Булева функция, представимая в виде линейного полинома Жегалкина, называется линейной.
Существует простой способ выражения любой булевой функции над базисом Жегалкина. Этот способ носит название метода неопределённых коэффициентов. Рассмотрим этот метод на примере:
Рассмотрим функцию 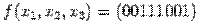 . В общем виде полином Жегалкина для этой функции имеет вид:
. В общем виде полином Жегалкина для этой функции имеет вид:
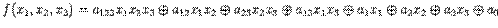
Вычислим все коэффициенты начиная с 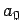 , последовательно подставляя в полином известные значения функции f:
, последовательно подставляя в полином известные значения функции f:

Таким образом, функция имеет вид:
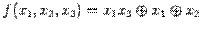
и не является линейной.
Теорема Поста
Существует метод проверки полноты системы, называемый теоремой Поста. Она основывается на выделении пяти классов Поста булевых функций:
Дата добавления: 2021-07-22; просмотров: 770;











