Класс линейных функций
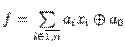 , т.е. функция представима в виде полинома Жегалкина первой степени.
, т.е. функция представима в виде полинома Жегалкина первой степени.
Можно доказать, что все эти классы являются замкнутыми, т.е. любая комбинация функций из одного класса остаётся в том же классе.
Теорема (Поста): система булевых функций полна тогда и только тогда, когда она целиком не лежит ни в одном из классов Поста. теорема Поста, которая гласит: для того чтобы система функций была базисной, необходимо и достаточно, чтобы она включала в себя хотя бы одну функцию, не принадлежащую 0, 1, 2, 3 и 4 классам
Рассмотрим пример: 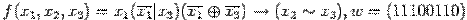 .
.
Необходимо проверить полноту системы 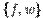 .
.
Функция f принимает следующие значения: 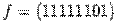 . Проверка принадлежности первых четырёх классов поста может быть проведена очень быстро. Для проверки линейности построим представление данных функций в виде полинома Жегалкина:
. Проверка принадлежности первых четырёх классов поста может быть проведена очень быстро. Для проверки линейности построим представление данных функций в виде полинома Жегалкина:
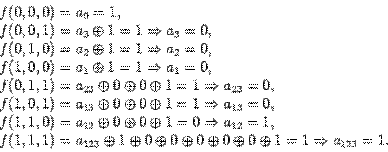
Поучается, что 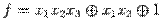 нелинейна.
нелинейна.
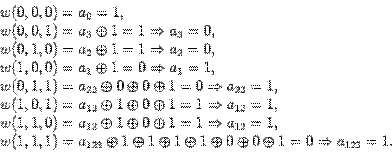
Поучается, что 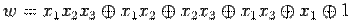 нелинейна.
нелинейна.
Принадлежность классам Поста обобщим в таблице:
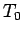
| 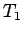
| 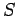
| 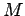
| 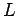
| |
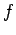
| - | + | - | - | - |
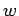
| - | - | - | - | - |
Система функций 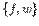 является полной, более того, полной является уже система
является полной, более того, полной является уже система 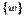 .Выразим стандартный базис
.Выразим стандартный базис 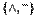 через функцию
через функцию 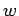 . Воспользуемся тем, что
. Воспользуемся тем, что 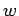 не сохраняет ни 0, ни 1, значит:
не сохраняет ни 0, ни 1, значит:
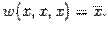
Так как 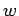 -- несамодвойственна, выразим константы через отрицание. Для этого найдём такой вектор
-- несамодвойственна, выразим константы через отрицание. Для этого найдём такой вектор 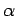 , что
, что 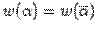 . Видно, что это выполняется при
. Видно, что это выполняется при 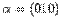 . Значит,
. Значит, 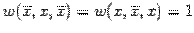 . Тогда 0 можно получить с помощью отрицания.
. Тогда 0 можно получить с помощью отрицания.
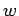 -- нелинейна, выразим коньюнкцию из полинома Жегалкина этой функции. Можно получить, что
-- нелинейна, выразим коньюнкцию из полинома Жегалкина этой функции. Можно получить, что 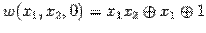 . Тогда
. Тогда
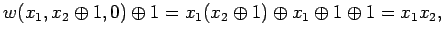
откуда 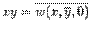 .
.
Дата добавления: 2021-07-22; просмотров: 552;











