Выравнивание уровней жидкости в резервуарах

Рассмотрим процесс выравнивания уровней жидкости в двух резервуарах, соединенных между собой трубопроводом, площадь сечения которого ω₀ (рис. 7.10).

На трубопроводе расположен затвор. Изначально уровень жидкости в одном резервуаре (левом на рис.7.10) находится на высоте z₁ относительно некоторой плоскости сравнения, а уровень жидкости в другом резервуаре – на высоте z₂, разность уровней (начальный напор) – H. Предположим, что в некоторый момент времени затвор мгновенно открывается. Жидкость начнет переливаться из одного резервуара в другой. За некоторый малый промежуток времени dt уровень жидкости в одном из резервуаров понизится на dz₁, а уровень жидкости в другом резервуаре повысится на dz₂.

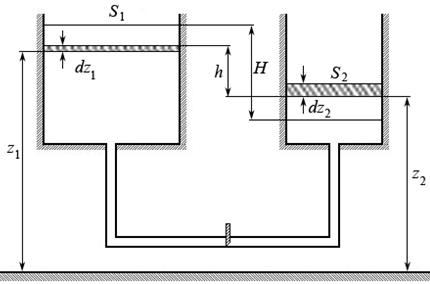
Рис. 7.10

Условие баланса объемов жидкости в резервуарах за промежуток времени dt запишется как

,

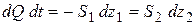где S₁ и S₂ – площади поверхности жидкости в резервуарах;

dQ – расход жидкости в трубопроводе.

Знак «минус» указывает на понижение уровня жидкости в первом резервуаре.

Это уравнение можно представить в виде двух равенств

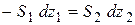	,	(7.6)
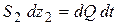	.	(7.7)

Действующий напор в каждый момент времени будет равен (рис. 7.10):

.

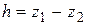Продифференцировав это выражение, получим

.

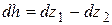Выразим dz₁ из равенства (7.6):

.

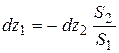Тогда

,

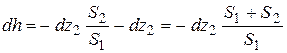откуда

.

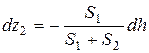Подставим полученное выражение в уравнение (7.7):

.

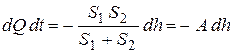Здесь введено обозначение 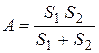– приведенная площадь поверхностей жидкости в резервуарах.

С другой стороны, расход жидкости, протекающей по трубопроводу, определяется формулой (6.13). Используя ее, для движения жидкости по трубопроводу при действующем текущем значении напора, равном h, можно записать

.

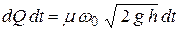Сравнивая два последних равенства, получим

,

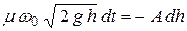откуда

.

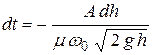Интегрируя это соотношение в пределах времени от 0 до t и соответствующих этим моментам времени напоров H и h, получим

.

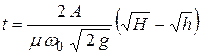(7.8)

Интегрируя, мы считали коэффициент расхода μ постоянным.

Формула (7.8) позволяет определить время выравнивания уровней жидкости в резервуарах. Это время T наступает, когда текущий напор h становится равным нулю. Тогда

.

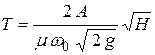Рассмотрим несколько частных случаев.

Пусть наполнение второго резервуара происходит из подводящего канала, имеющего 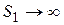. В этом случае

,

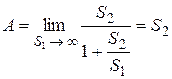и время наполнения резервуара

.

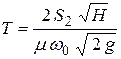В случае опорожнения первого резервуара в канал с 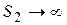получим:

,

.

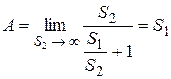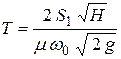Получаем формулу, аналогичную формуле (7.5) для опорожнения резервуара при переменном напоре.

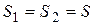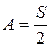В случае если , то и

.

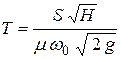В действительности время открытия затвора на трубопроводе не равно нулю. Пусть время открытия затвора равно t₀. Процесс расчета времени выравнивания уровней жидкости в резервуарах усложнится. Время выравнивания будет складываться из двух периодов:

· первый – от 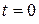до 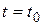, в это время коэффициент расхода μ будет изменяться во времени по мере открытия затвора;

· второй – от 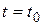до 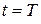, в этот период .

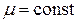Для первого периода, используя формулу (7.8), можно записать

.

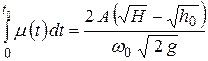Здесь h₀ – напор, соответствующий моменту времени t₀.

Поскольку 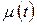определяется, как правило, эмпирическим путем, интеграл в левой части этого равенства вычисляется численно или одним из приближенных методов.

Для второго периода при постоянном значении μ будет справедлива формула

.

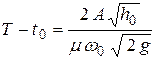Таким образом, время полного выравнивания уровней жидкости в резервуарах

.

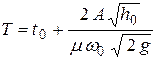(7.9)

В практических расчетах время открытия затвора t₀ обычно задается. Тогда из формулы (7.8) при известном начальном напоре H и времени t₀ находится значение h₀, и затем из уравнения (7.9) находится время выравнивания T.