Основные критерии работоспособности деталей машин
Ряды предпочтительных чисел
Стандарт (ГОСТ) – это технический закон, соблюдение которого является безоговорочным и обязательным.
Одной из основ стандартизации являются ряды предпочтительных чисел, получившие широчайшее применение в машиностроении для размеров, передаточных чисел, нагрузок, мощностей, скоростей и других параметров.
По ГОСТ 8032-84 принято пять рядов чисел геометрической прогрессии
| |
чают буквой R (по имени автора, Шарля Ренара, 1879 г.) и цифрой показателя n:
| n | |||||
| φ | 1,6 | 1,25 | 1,12 | 1,06 | 1,03 |
| ряд | R5 | R10 | R20 | R40 | R80 |
Наиболее распространенным является "средний" ряд чисел R20:
| 1 | 1,12 | 1,25 | 1,4 | 1,6 | 1,8 |
| 2 | 2,24 | 2,5 | 2,8 | 3,15 | 3,55 |
| 4 | 4,5 | 5 | 5,6 | 6,3 | 7,1 |
| 8 | 10. |
Примечание. Подчеркнутые цифры образуют ряд R10.
Предпочтительные числа других порядков можно получить переносом запятой в любую сторону, т.е. умножением на 10, 102… 10–2, 10–1 и т.д.
На основе рядов предпочтительных чисел построены стандарты конкретных объектов. Например, по ГОСТ 6636-69 ряды нормальных линейных размеров обозначают Ra (Ra10, Ra20 и т.д.).
Зная числа рядов, можно иметь "в голове" параметры многих стандартов.
Основные критерии работоспособности деталей машин
Критерий – это "мерило значения чего-либо", граница допустимости решения, ограничение целевой функции.
Важнейшими критериями работоспособности деталей машин являются прочность, жесткость, износостойкость, теплостойкость, вибрационная устойчивость.
При конструировании работоспособность деталей обеспечивают выбором материала и расчетом размеров по основному критерию. Выбор критерия обусловлен характером воздействия нагрузки, среды и вызываемым видом отказа.
В настоящее время самым распространенным критерием работоспособности является прочность.
Прочность – это способность детали сопротивляться разрушению или потере формы под действием приложенных к детали нагрузок. Этому критерию должны удовлетворять все детали и узлы.
На основании принципа независимости действия сил любое сложное напряженное состояние можно разложить на простые виды: растяжение, сжатие, изгиб, сдвиг (кручение), срез – это внутренние напряжения в сечениях деталей.
На поверхности соприкосновения (контакта) двух деталей под нагрузкой возникают поверхностные напряжения. Если размеры площадок контакта одного порядка с другими размерами деталей, то говорят о напряжениях смятия sсм. Если хотя бы один из размеров площадки контакта существенно мал по сравнению с другими размерами, то возникают контактные напряжения.
Исследованием контактных напряжений занимался Генрих Герц (Hertz). В его честь эти напряжения обозначают с индексом "Н": sН, τН.
В "Теории упругости" различают две контактные задачи:
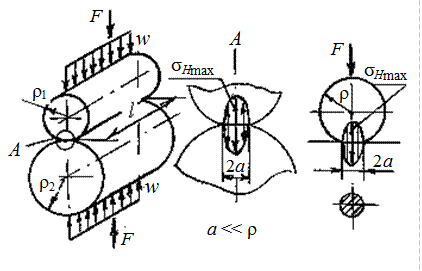
а) с первоначальным (до приложения нагрузки) контактом по линии,
| |
Вследствие упругих деформаций под действием сжимающей нагрузки w = F / l линия контакта переходит в узкую полоску шириной 2а (2а << r), на которой возникают контактные напряжения sН, изменяющиеся по эллиптическому закону.
Формула Герца для первоначального контакта по линии: sН = ZE (w / rпр)1/2 £ [sH] , (1.1)
где w = F / l – удельная (на 1 мм длины линии контакта) линейная нагрузка, Н/мм; ZE – коэффициент влияния механических свойств материалов деталей;
|
Рис. 1.1 Рис. 1.2
б) с первоначальным контактом в точке, например, сжатие шара на плоскости (рис. 1.2).
Числовые значения sН намного превышают другие виды напряжений и даже пределы текучести sТ и прочности sВ. Например, в подшипниках качения sНmax = = 4200 МПа, а sТ = 1700 МПа и sВ = 1900 МПа у стали ШХ15 для них.
Кроме sН , в зоне контакта возникают также касательные напряжения
tНmax = 0,3sНmax в точке, отстоящей от поверхности контакта на глубину 0,78а.
Отсутствие мгновенного разрушения объясняется тем, что в зоне действия sН и tН материал находится в условиях всестороннего объемного сжатия.
Рассчитав величины отдельных составляющих напряжений, по принципу суперпозиции (наложения) с учетом векторного характера, можно определить суммарное или эквивалентное напряжение sЕ. Например, для совместных напряжений изгиба s и кручения t: sЕ = (s2 + 3t2) 1/2 £ [s].
По критерию [s] делают оценку прочности изделия.
Дата добавления: 2021-07-22; просмотров: 439;