Задачи теории расписаний и раскраска графа
Задачи теории расписаний тесно связаны с задачей раскраски графа. Задачи составления расписания могут быть представлены графами, где вершины обозначают некоторые мероприятия (лекции / экзамены), а ребра обозначают конфликты между мероприятиями (например, тогда, когда студенты должны одновременно принимать участие в обоих мероприятиях).Построение расписания без конфликтов может быть смоделировано в виде задачи о раскраске графа. Задача состоит в том, чтобы раскрасить вершины графа так, чтобы никакие две смежные вершины не были окрашены одним цветом. Каждый цвет соответствует периоду времени в расписании. В литературе имеются различные эвристики для построения расписаний без конфликтов, основанные на раскраске графа.
Задача о раскраске графа («правильная раскраска вершин») является хорошо известной NP-полной задачей [4]. Она может быть сформулирована следующим образом: для простого неориентированного, но не обязательно связного графа G = (V, E) и целого число 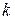 , решить, возможно ли назначить
, решить, возможно ли назначить 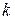 цветов
цветов 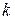 вершинам
вершинам 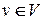 так, что никаким двум смежным вершинам
так, что никаким двум смежным вершинам 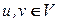 не присваивается одинаковый цвет. Задача о раскраске графа имеет ряд приложений, начиная от составления университетских расписаний и задач назначения частот в сотовых сетях, до распределения в регистров в компиляторах.
не присваивается одинаковый цвет. Задача о раскраске графа имеет ряд приложений, начиная от составления университетских расписаний и задач назначения частот в сотовых сетях, до распределения в регистров в компиляторах.
Так как 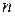 цветов всегда будет достаточно для раскраски любого графа с
цветов всегда будет достаточно для раскраски любого графа с 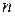 вершинами, простая модель ЦЛП для раскраски графа может быть получена с помощью введения двух следующих бинарных переменных:
вершинами, простая модель ЦЛП для раскраски графа может быть получена с помощью введения двух следующих бинарных переменных: 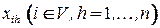 , причем
, причем 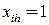 , если вершине
, если вершине 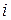 присваивается цвет
присваивается цвет 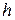 , и
, и 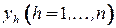 , причем
, причем 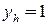 , если цвет
, если цвет 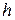 используется в решении. Модель ЦЛП для задачи раскраски графа имеет вид:
используется в решении. Модель ЦЛП для задачи раскраски графа имеет вид:
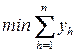
при ограничениях
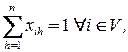
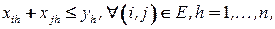
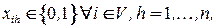
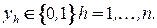
Дата добавления: 2016-06-05; просмотров: 2957;











