Расчётно-графическая задача №2
Балки
На статически неопределимую балку из прокатного профиля действует нагрузка. Необходимые данные приведены на рис.5.2 и в таблице 5.2.
Таблица 5.2
| Номер | L1, | L2/L1 | Номер | Р/ql1 | М*/ql2 | |
| строки | схемы | м | двутавро- | |||
| (см. рис. 5. 2) | вой балки | |||||
| 0,1 | 0,02 | |||||
| 0,8 | 0,2 | 0,03 | ||||
| 3,6 | 0,6 | 0,3 | 0,04 | |||
| 4,5 | 0,8 | 0,4 | 0,05 | |||
| 3,8 | 0,7 | 0,5 | 0,05 | |||
| 0,6 | 0,6 | 0,04 | ||||
| 0,5 | 0,7 | 0,03 | ||||
| 0,6 | 0,8 | 0,02 | ||||
| 0,9 | 0,04 | |||||
| 1,2 | 1,0 | 0,03 | ||||
| е | а | б | в | д | г |
 |
Требуется:
1. Выполнить расчет статически неопределимой балки, выразив нагрузки через один параметр 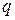 , Р или М* и построить эпюры бающих моментов М* и поперечных сил Q.
, Р или М* и построить эпюры бающих моментов М* и поперечных сил Q.
2. Выполнив анализ эпюры М* определить нагрузку, при которой возникнет текучесть в наиболее нагруженном сечении балки.
3. Задавшись кинематически возможной схемой разрушения балки определить предельную нагрузку.
4. Построить в масштабе схему балки и изобразить на чертеже необходимые эпюры внутренних усилий.
Указание.
При определении нагрузки текучести принимается Мт = σnWx, где Wx приведены в сортаменте прокатного профиля.
При определении предельной нагрузки принимается Мпр = σnWпл, где пластический момент сопротивления 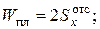
Расчетно-графическая задача №3
Рамы.
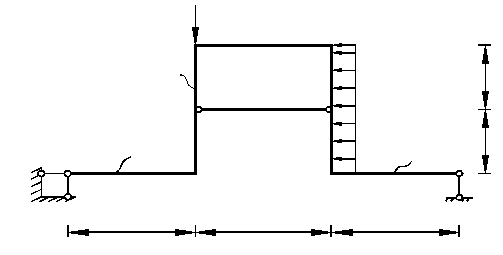
Для статически неопределимой рамы, изображённой на рис.5.3, определить нагрузку текучести и предельную нагрузку, считая нагру-жение простым. Напряжение текучести σт принять равным 100 мПа.
Требуется:
1. Выполнить расчёт статически неопределимой рамы (см. рис.5.3) в соответствии с исходными данными, заданными в таблице 5.3.
2. Подобрать из условия прочности
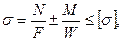
где F = b ∙ h, W = b ∙ h2/6, размеры квадратного или прямоугольного поперечного сечения (b ∙ h) вертикальных и горизонтальных стержней рамы.
Указание. Задача вычисления размеров поперечного сечения сводится к решению кубического уравнения. Однако эту задачу можно упростить, найдя отдельно площадь от изгиба и от растяжения (сжатия), а затем сложить эти площади. Можно решить эту задачу и путём подбора.
3. Выразив нагрузку q, Р через один параметр, определить их значения qт, Рт, при которых начнут возникать пластические деформации в наиболее нагруженном сечении рамы. При этом Мт = σтWx, где W = b ∙ h2/6.
4. Выполнив анализ напряжённого состояния и составив схему разрушения рамы, определить предельные значения нагрузок
qпр, Рпр. При этом Мпр = σтWпл, где Wпл = b ∙ h2/6.
5. Сделать чертёж, на котором изобразить в масштабе раму и все
необходимые эпюры внутренних сил.
Таблица 5.3.
| Номер | L | H | P | q | Ir/IB | h/b | |
| строки | схемы | м | м | кН | кН/м | ||
| (см. рис.5.3) | |||||||
| 1,2 | |||||||
| 2,4 | 1,5 | ||||||
| 5,2 | |||||||
| 6,2 | |||||||
| 0,5 | |||||||
| 2,5 | 1,5 | ||||||
| 3,5 | 4,2 | 0,5 | |||||
| 4,5 | |||||||
| 1,2 | |||||||
| 2,2 | |||||||
| е | а | б | в | г | д | д |
 | |||
 |

| |||||||
| |||||||
| |||||||
 |
5.2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
Пример 1. Рассмотрим деформирование прямолинейного стержня при растяжении – сжатии.
Стержень переменного поперечного сечения (рис.5.4,а) площадью F, длиной L, состоящий из трёх участков, нагружен в сечении С силой Р. Торцы А и В закреплены неподвижно. Условная диаграмма растяжения
σ – ε материала схематизирована в виде диаграммы без упрочнения (рис.5.4, в).
Исходные данные следующие (рис. 5.4, а):
а = 0,1 м; b = 0,04м; с = 0,08м; L = а + b + с; Е = 2∙ 1011 Па; F = 1 см2; σтс = – 280 ∙106 Па; σтр= 210 ∙ 106Па.
Исследовать деформацию стержня в пределах и за пределами упругости.
I. Решение упругой задачи.
Выполним расчёт статически-неопределимого стержня. Разрежем мысленно стержень у торца А, приложив в сечении неизвестную реакцию RА (рис. 5.4,б). У торца В возникает реакция RВ. Мы видим, что неизвестных сил две, а статических уравнений равновесия можно записать только одно - такая система является статически неопределимой.
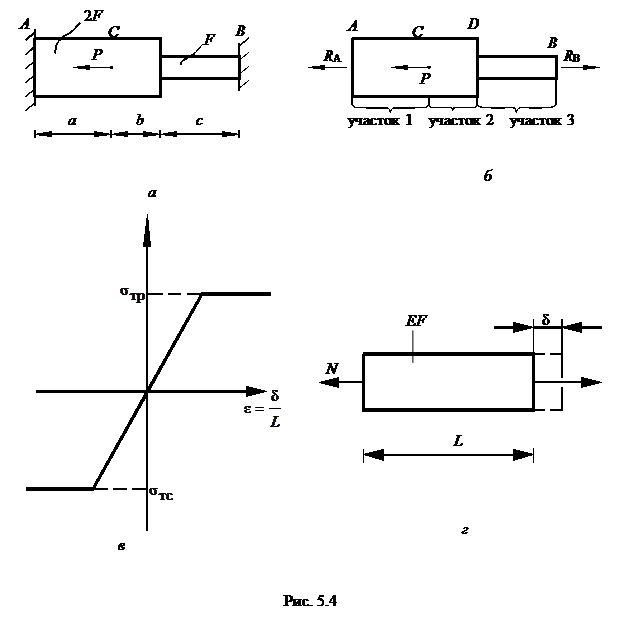
Известно, что если продольная сила N на участке длиной L постоянная (рис.5.4,г), то удлинение или укорочение этого участка стержня жёсткостью ЕF можно определить по формуле:
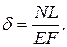
 |
Допустимой силы мы пока не знаем, для удобства пусть она равна параметру Р.
Теперь, если закрепить только левый торец стержня от смещения (рис.5.5,а), то от силы Р стержень укоротится на величину
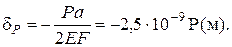
 | |||
|
Аналогично от правой реакции Rb стержень удлинится (рис.5.5,б) на величину δ:
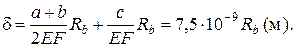
Так как сечение В неподвижно, то сумма этих перемещений должна равняться нулю δp + δ = 0. Отсюда определяем возникающую в сечении В реакцию:
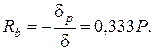
Окончательная эпюра усилий (рис.5.5, д) в упругой статически неопределимой задаче складывается из эпюры N (рис.5.5,г), умноженной на 0,ЗЗЗ Р и эпюры NР (рис.5. 5,в).
Итак , усилия будут такими:
N1= – P + RB; N1= – 0,667 P ; - участок 1
N2 = RB N2 = 0,333 P; - участок 2
N3 = RB N3= 0,333 P; - участок 3
Упругие удлинения участков будут равны :
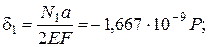
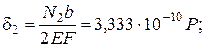
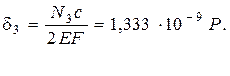
Сумма удлинений всех участков , равная нулю, должна являться проверкой:
2. Решение упруго – пластической задачи.
Выполним расчет по предельному состоянию. Из условия возникновения пластических деформаций
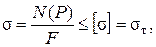
определим усилия, от которых эти деформации возникнут на участках 1,2,3:
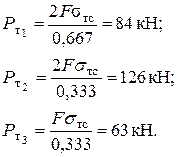
Отсюда видим, что пластические деформации в первую очередь возникнут на участке 3 при Р = Ртз.
При дальнейшем увеличении силы Р, напряжения на участке 3 увеличиваться не будут в соответствии с диаграммой деформирования материала без упрочнения ( рис. 5.4,в), а останутся постоянными и равными напряжению текучести при сжатии (рис. 5.6,а); усилие также будет постоянным: Nтз = σтр F =21 кН .
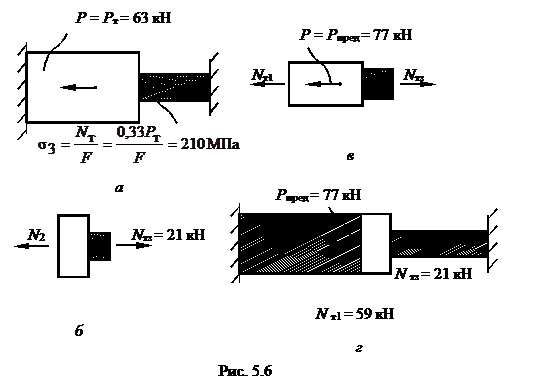
Участки стержня, на которых возникнут пластические деформации в дальнейшем на рисунках будут показаны заштрихованными.
В данной задаче усилие на участке 2 будет всегда равным усилию на третьем участке – это видно из равновесия отсеченной части этих двух участков ( рис. 5.6, б):
N2 = Nтз.
Напряжение всегда будет оставаться меньше напряжения текучести, поэтому этот участок будет всегда упругим.
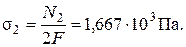
Пластичность на первом участке возникнет тогда, когда
Nт1 = σтс2F = – 56 кН.
Из уравнения равновесия (рис.5.6,в) определим предельную нагрузку;
Рпоед = Nтз – Nт1 = 77 кН.
При этом значении силы Р пластичность возникает на участках 1 и 3. Большую силу конструкция не выдержит. Участок 2 останется упругим (рис.5.6,г).
По методу предельного состояния предельная нагрузка уменьшается на коэффициент запаса, равный, например n =1,4. Тогда допускаемая нагрузка равна
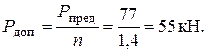
По методу допускаемых напряжений предельной нагрузкой является сила, от которой впервые возникла пластичность; тогда допускаемая нагрузка будет вычисляться по формуле
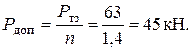
Сопоставляя значения допускаемых нагрузок, заключаем , что метод расчета по предельному состоянию вскрывает дополнительные прочностные ресурсы , не используемые в методе допускаемых напряжений.
Пример.2 Исследуем процесс деформирования шарнирно-стержневой системы, состоящей из четырех одинаковых стержней, поддерживающих абсолютно жесткую на изгиб балку (рис.5.7,а) нагруженную силой Р методом последовательного нагружения. Стержни деформируются согласно условной диаграмме Прандтля (рис.5.7,б)
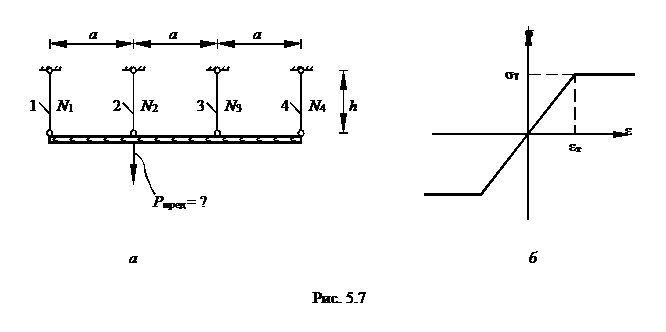 |
Общую картину поведения статически неопределимой
упруго – пластической системы в течение всего процесса нагружения может дать серия расчётов упругих систем, получающихся из заданной путем последовательного исключения связей, пришедших в состояние текучести. Первоначально система (рис.5.7,а) дважды статически неопределима. Предельная нагрузка Рпред ещё неизвестна, поэтому усилия в стержнях 1 – 4 в начале примем нулевыми:
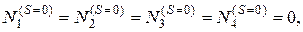
где S-шаг нагружения.
На первом шаге деформирования S = 1 загрузим систему по направлению действия силы Рпред приращением нагрузки ∆Р1 (рис.5.8). Стержневая система работает как полностью упругая, её статический расчёт можно выполнить с помощью метода сил (см. дополнение 1), который даёт следующие усилия в стержнях (рис.5. 8,а):
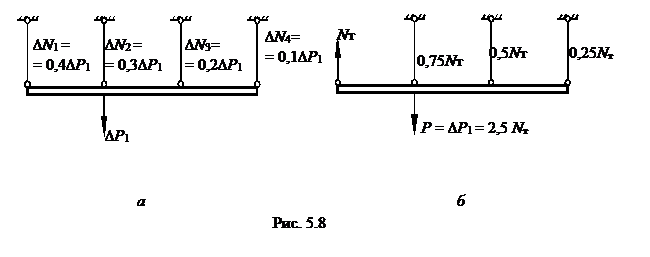 |
∆N1 = 0,4 ∆P1; ∆N2 = 0,3 ∆P1; ∆N3 = 0,2 ∆P1; ∆N4 = 0,1 ∆P1.
Наибольшее усилие ∆N1 = 0,4 ∆P1 возникает в первом стержне. Приравняв N1 усилию Nт = σт F, где F - площадь поперечного сечения, определить значение ∆P1, при котором возникнут пластические деформации в первом стержне:
∆N1= 0,4 ∆P1 = Nт 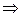 ∆Р1=Nт/ 0,4 =2,5 Nт .
∆Р1=Nт/ 0,4 =2,5 Nт .
Таким образом, если к системе приложить силу Р = ∆Р1 = 2,5Nт то получим распределение накопленных усилий в стержнях на первом шаге нагружения (рис.5. 8,6):
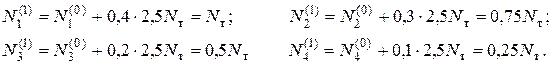
Анализируя распределение усилий в стержнях отметим, что в первом стержне усилие достигло значения Nт и далее не будет увеличиваться, а остальные стержни работают в упругой стадии согласно диаграмме Прандтля (рис.5. 7,б).
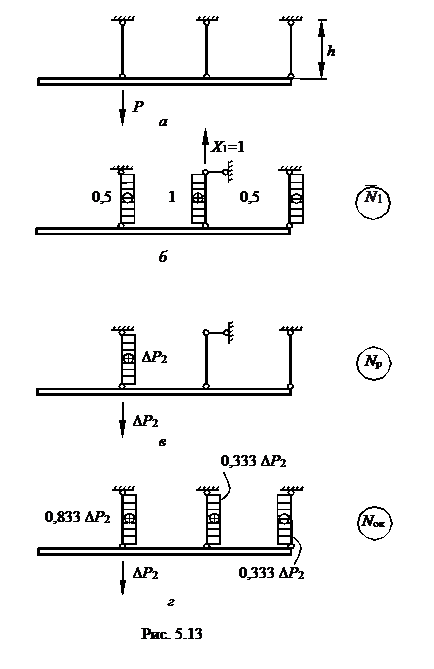
На втором шаге деформирования S = 2 нагрузим стержневую с тему (однажды статически неопределимую) силой ∆Р2 (рис.5.9а) выполним расчёт методом сил (см. дополнение 2).
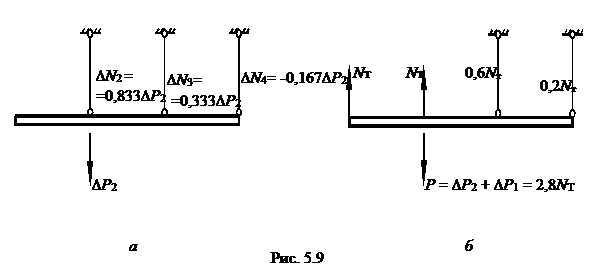 |
Упругий расчёт даёт следующие приращения усилий в стержнях:
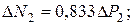
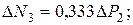
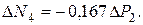
Наиболее натруженным оказался стержень 2, поэтому в нем усилие достигнет Nт:
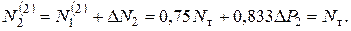
Отсюда
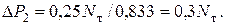
Таким образом, если к стержневой системе приложить силу 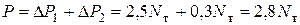 (рис.5.9,б), получим накопленные усилия в стержнях на втором шаге нагружения:
(рис.5.9,б), получим накопленные усилия в стержнях на втором шаге нагружения:
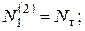
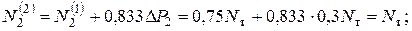
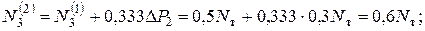
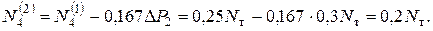
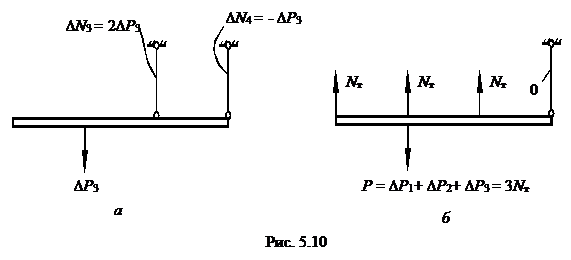
На третьем шаге S=3 нагружения рассмотрим расчет статически определимой системы, к которой приложены приращение ∆Р (рис.5.10, а).
Приращения усилий определяется из уравнений равновесия и равны:
∆N3 =2∆Р3; ∆N4 = – ∆Р3.
Приравнивая суммарное усилие в стержне 3 усилию текучести Nт
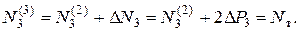
или
0,6NT +2∆P3 =Nт,

получим
∆Р3=0,4 Nт/2 = 0,2 Nт
Таким образом, если к стержневой системе приложить силу
Р = ∆Р1+∆Р2+∆Р3 = 3Nт, то получим распределение накопленных усилий в стержнях на третьем шаге нагружения (рис.5.10,б):
 |
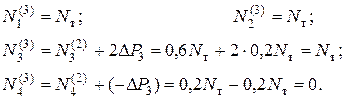
Таким образом Рпред - полная предельная нагрузка стержневой системы, то есть несущая способность последней равна Рпред= ЗNт. Если
σт = 250 мПа, а F = 1 см2, то Рпред= Зσт F = 75 кН.
Определим абсолютную деформацию ∆h2 стержня 2, под которым приложена сила Р в конце каждого шага нагружения (см. дополнение 3):
График зависимости абсолютной деформации от величины достигнутой силы Р показан на рис. 5.11.
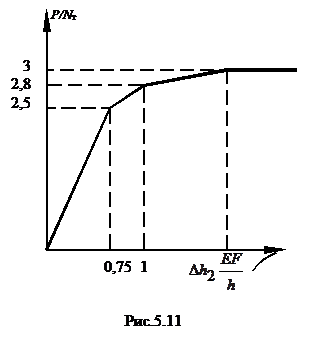
Зависимость изображается ломаной линией, которая при достижении предельного равновесия Р = ЗNт становится горизонтальной.
Проведенный расчёт даже
для такой простой системы
оказывается громоздким, но
зато он даёт возможность
описать всё поведение конструкции
в процессе её нагружения.
Дополнение 1. Расчёт стержневой системы методом сил. Для симметричной системы выберем
основную систему метода сил
|
с использованием групповых неизвестных (рис.5.12,а). Единичные и грузовые эпюры показаны на рис.5.12(в – д). Окончательная эпюра приведена на рис. 5.12,е.
δijXj+∆iр= 0; i, j = 1, 2.; 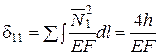 ;
;
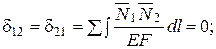
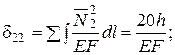
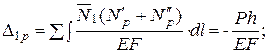
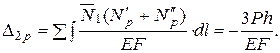


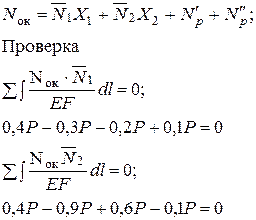
Дополнение 2. Расчет однажды статически неопределимой системы (рис.5.13,а). Основная система и эпюра N изображены на рис. 5.13, б, грузовая – на рис. 5.13, в.
δ11Х1 + ∆1р=0;
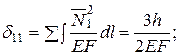
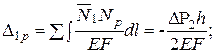
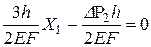 .
.
Отсюда 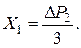
Окончательная эпюра
Nок = 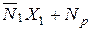
Показана на рис. 5.13,г.
Дополнение 3 Требуется определить перемещение в точке приложения силы Р. Чтобы определить перемещение, нужно в любой основной системе метода сил по направлению искомого перемещения приложить единичный груз Х1= 1 и построить эпюру 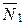 (рис. 5.14, а). Интегралы
(рис. 5.14, а). Интегралы 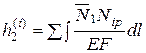 дают значения перемещений по искомому направлению.
дают значения перемещений по искомому направлению.
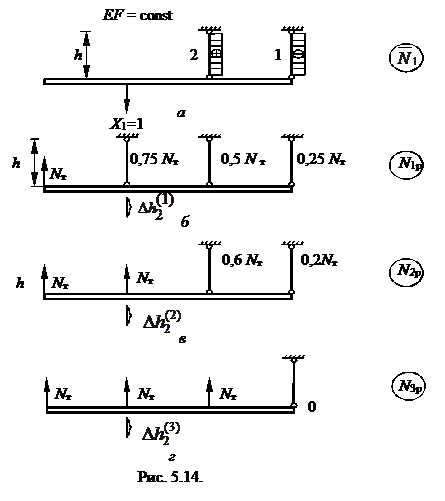 |
|
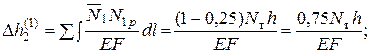
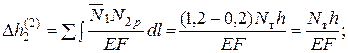
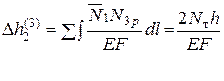
Пример 3. Определим состояние предельного равновесия шарнирно-
стержневой системы кинематическим методом.
Рассмотрим шарнирно – стержневую систему (рис.5.15,а) и будем читать, что стержни одинаково сопротивляются растяжению и сжатию, а балка абсолютно жёсткая на изгиб. Кроме того, упругие деформации стержней настолько малы, что ими можно пренебречь по сравнению деформациями текучести.
Зададимся тремя кинематически возможными формами разрушения системы, а именно поворотами балки на малый угол вокруг точек А, С, Д и из условий равновесия определим величину нагрузки Р.

Из рис.5.15,6 записываем
ΣmA=0; l – Nт · (l+2l+3l) = 0 ; →P = 6 Nт.
Из рис.5. 15,в записываем
Σmс = 0; Nт · 2l + Nт l+ Nт l –Рl) = 0 ; →= 0; → P =3Nт .
Видим, что минимальное усилие Р усилие Р=Рпред равное 3Nт получается получается при повороте балки вокруг точки Д, то есть, когда в состоянии тякучести находятся первые три стержня.
Дата добавления: 2021-07-22; просмотров: 463;











