Шарнирно-стержневые системы

РАСЧЁТ КОНСТРУКЦИЙ ЗА ПРЕДЕЛОМ УПРУГОСТИ

Задачи, решённые в главе, посвящены основам расчёта конструк­ций с учётом возникновения в них пластических деформаций. Определяются нагрузки, при которых возникают пластические деформации и нагрузки предельного состояния. В первом пункте настоящей главы в примере 1 анализируется упругопластический расчёт стержня ступенчато-переменной жесткости с разгрузкой. Шарнирно-стержневые системы рассматриваются в примерах 2 – 3. Причём, в первом из них применяется шаговый процесс нагружения, позволяющий описать поведение конструкции за весь период деформирования. Во втором примере используется более простой, кинематический метод определения предельного состояния. Пункт второй посвящен кручению круглых валов. В примере 1 определяется предельный крутящий момент и деформированное состояние круглого вала. Аналогичная задача для статически неопределимого вала ступенчато-переменной жесткости решается в примере 2. Примеры 1 – 2 посвящены статически определимым балкам, в которых изучается распределение зон пластичности по объему конструкций. В примерах 3 – 5 проводится методика определения предельных нагрузок в статически неопределимых балках. Примеры 6 – 7 затрагивают определение нагрузок текучести и предельных нагрузок в простейших рамах.

В начале главы приводятся схемы заданий для выполнения расчетно-графических работ. Исходные данные берутся в строгом соответствии с личным номером (шрифтом) зачетной книжки. Для этого три последние цифры своего шифра написать дважды, а затем под шестью цифрами подписать буквы а,б,в,г,д,е. Например, при шифре 436628 это будет выглядеть так:

6 2 8 6 2 8

а б в г д е

Тогда цифра над буквой а укажет, какую строку следует брать из столбца а; под буквой б и т.д. Преподаватель может выдавать другие варианты заданий по необходимости.

В конце главы приведены вопросы для самоконтроля, подобранные из перечня экзаменационных вопросов. С замечаниями и вопросами по задачам обращаться на кафедру технической механики: ауд. Д – 204 тел. 629 –593.

5.1 РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ

Расчётно-графическая задача № 1

Шарнирно-стержневые системы

Абсолютно жёсткий на изгиб брус (рис.5.1), имеющий одну шарнирно-неподвижную опору в точке А и прикреплённый двумя тягами из стали, нагружён переменной по значению силой Р. Площадь попереч­ного сечения тяг F₁ и F₂, модуль упругости и предел текучести мате­риала тяг

Е = 2 ∙ 10⁵ мПа и 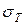= 240 мПа; допускаемое напряжение [σ] = σ_Т /k,

где k– коэффициент запаса прочности k = 1,5.

Требуется:

1. Сделать чертёж всей конструкции по заданным размерам, соблю­дая масштаб.

2. Найти в зависимости от силы Р значения усилий в тягах.

3. Определить в процессе увеличения силы Р её значение Р_т, при котором напряжение в одной из тяг достигнет предела текучести.

4. Определить в процессе дальнейшего увеличения силы Р её пре­дельное значение Р_пред в предположении, что несущая способность обеих тяг исчерпана.

5. Найти значения грузоподъёмности из расчёта по методам допу­скаемых напряжений и предельного состояния при одном и том же коэффициенте запаса прочности.

Указание. Диаграмма зависимости между напряжением и удлине­нием принимается в виде упругопластической зависимости Прандтля без упрочнения. Исходные данные взять из таблицы 5.1.

Таблица 5.1

	Номер	F1	F2	а	b	с	l1	l2
	строки	столбца	cм2	см2 см	м	м	м	м	м
		(см.рис.5.1)
					1,1	1,0	1,5	0,8	0,6
					1,2	1,9	1,4	0,9	0,8
					1,3	1,8	1,3	1,2	1,0
					1,8	1,7	1,2	1,4	1,2
					1,6	1,6	1,1	1,6	1,4
					1,5	1,5	1,0	1,8	1,5
					1,7	1,4	1,6	2,0	1,6
				1,9	1,3	1,7	2,1	1,8
				1,4	1,2	1,8	0,6	2,0
				1,0	1,1	1,9	2,2	2,2
	е	а	б	д	г	в	е	а