НОРМИРОВАНИЕ ТОЧНОСТИ УГЛОВЫХ РАЗМЕРОВ

Единицами измерения углов могут быть следующие величины:

– международные единицы - радиан и стерадиан (ГОСТ 8.417);

– практическая единица в градусной мере (градус, минута, секунда);

– метрические единицы (мкм; мм), учитывающие соотношение угловых и линейных единиц на заданной длине измерения [1,2,4,6].

Нормальные ряды углов общего назначения даны в ГОСТ 8908 (табл. 1.9), а углы конусов нормальных конусностей и области их применения даны в табл. 1.10.

Допуск угла обозначается – АТ. Установлено 17 степеней точности в порядке уменьшения точности: 1, . . . ,17.

Степени точности АТ1 ¸ АТ5 применяются для углов измерительных средств и калибров и требуют тонкого шлифования с последующей доводкой.

Степени точности АТ4 ¸ АТ12 используются для сопрягаемых углов и конусов, остальные – для углов с неуказанными допусками.

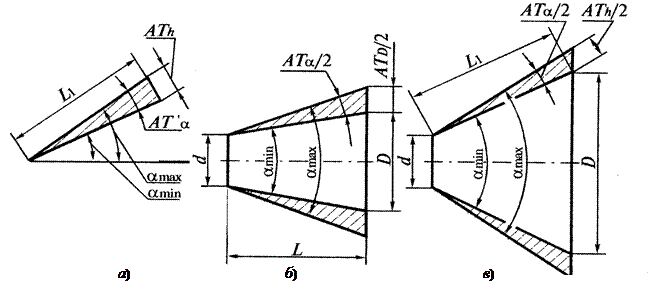
Допуски углов назначаются в зависимости от номинальной длины меньшей стороны угла, так как чем меньше длина, тем труднее изготовить и измерить угол (рис. 1.8.):

- АТ_a– в угловых единицах рад; мкрад;

- АТ′_a– округлённое значение допуска угла в градусной мере; (360° = 2p = 6,2831рад; 1° = 2p/360 = 0,01743рад; 1рад = 360/2p =57° 17′43");

- АT_h; АТ_D – допуски угла в метрической системе единиц (мкм).

- АТh – длина противолежащего отрезка на перпендикуляре к стороне угла на расстояние L от вершины угла (рис. 1.8, а и рис. 1.8, в);

- АТ_D – разность диаметров в двух сечениях конуса на расстояние L между ними (рис. 1.8, б).

Различают три основных типа расположения поля допуска относительно номинального угла: плюсовое (+АТ_a) ; минусовое (-АТ_a); симметричное (±АТ_a/2), (рис. 1.9 и 1.10).

Допуски углов даны в табл. 1.10. На чертежах указываются числовое значение допуска угла с учётом знака, единица измерения, а также координаты расположения угла относительно оси или плоскости детали.

Конусность С определяется по формуле С=(D - d)/L=2tg(a/2).

Для малых углов (С£1:3): АT_D@ AT_h.

Связь между допусками углов в угловых и линейных единицах определяется по формуле: АТ_h=10^-3АT_aL , где AT_hв мкм; АТ_a – мкрад; L – мм

Для конусов с конусностью больше, чем 1:3, значение АТ_D определяется по формуле. АТ_D = АТ_h/cos(a/2), где a – номинальный угол конуса.

.

Рис. 1.8. Виды допусков углов:

а – допуск угла; б – конусность С £ 1:3; в – конусность С > 1:3

	а) б) в)

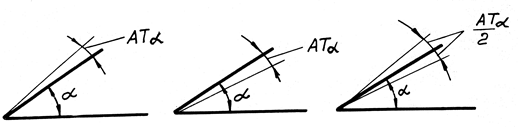Рис. 1.9. Типы расположения полей допусков для угла призматического элемента:

а – (a + АТ_a); б – (a – АТ_a); в – (a ± АТ_a/2)

	а) б) в)

Рис. 1.10. Типы расположения полей допусков для угла конуса:

а – (a + АТ_a); б – (a – АТ_a); в – (a ± АТ_a/2)

Т а б л и ц а 1.9