Проблема репрезентативности выборки

Задача индуктивной статистики – определять, достаточно ли велика разность между средними двух распределений для того, чтобы можно было объяснить ее действие независимой переменной, а не случайностью, связанной с малым объемом выборки, отсутствием репрезентативности.

Основная проблема репрезентативности выборки – величина и верность образцов. Величина представленности образцов зависит от степени однородности целого (чем однороднее целое, тем меньше требуется образцов); от численности категорий и классов, на которые подразделяются результаты исследования (чем их больше, тем больше должно быть образцов); от количества работников, привлеченных к исследованию; от финансирования.

Выборки называются статистически однородными, если их распределения сходны, а различия между ними пренебрежимо малы. В противном случае, когда различия велики, а сходство пренебрежимо мало, выборки статистически неоднородны.

В некоторых случаях исследователю приходится проверять гипотезы об однородности (неоднородности) через параметры, делая определенные допущения о виде распределения. Это делается не просто путем проверки сходства или различия средних арифметических значений, но с учетом того, что все распределения (кроме Пуассона) имеют два или больше параметров, к примеру, нормальное распределение Гаусса и гамма-распределение, которым следуют многие психологические и педагогические явления, являются двухпараметрическими. Поэтому вместо простой гипотезы о сходстве (различии) двух функций распределения необходимо проверять сложную гипотезу о сходстве двух средних арифметических и одновременно о сходстве двух дисперсий. Только такая гипотеза может быть адекватной в этом случае.

Размер выборки находится в зависимости от размера генеральной совокупности, подлежащей изучению, а также цели исследования. Когда цель исследования заключается в изучении состояния знаний ограниченного количества учащихся, например, одного класса, объем выборки не может превысить численность этого класса. В отдельных случаях объем выборки может быть меньше численности учащихся класса из-за того, что не учитываются результаты новеньких в данном классе, пропустивших много занятий по болезни.

При изучении больших по объему совокупностей проблема отбора решается с учетом количественной и качественной представительности выборки, это называется требованием репрезентативности.

Во-первых, необходимо определить минимальное число объектов, необходимых для того, чтобы при измерении их характерных особенностей начал действовать закон больших чисел, что именуется условием массовости выборки. Соблюдение данного условия необходимо для получения надежных выводов.

Во-вторых, необходимо обдумать соблюдение качественной представительности выборки. Под качественной представительностью выборки понимается подбор такой группы объектов, в которой отражены все основные свойства генеральной совокупности.

Репрезентативная выборка имеет достаточно большой объем и отражает основные свойства генеральной совокупности. Требование репрезентативности соблюдается лишь при случайном отборе объектов в выборке.

Метод случайного отбора характеризуется двумя отличительными особенностями: 1) каждый объект генеральной совокупности имеет одинаковый шанс быть избранным, 2) отбор одного объекта не имеет никакого влияния на отбор какого-либо другого объекта. К этим методам относятся следующие: простой случайный отбор, отбор методом случайных чисел, стратифицированный отбор, систематический отбор.

Простой случайный отбор применяется, когда выборка составляется из совокупности небольшого объема. В этом случае каждому элементу совокупности присваивается порядковый номер. Все номера записываются на одинаковые карточки, которые тщательно перемешиваются. Затем выбирается число карточек, требуемое объемом выборки. Выборку составят те объекты, чьи порядковые номера оказались на вынутых карточках.

Отбор методом случайных чисел отличается от предыдущего только процессом отбора карточек. При отборе карточек применяется таблица случайных чисел. С любого места таблицы выписываются столько случайных чисел, сколько объектов необходимо взять в выборку. Те объекты, порядковые номера которых соответствуют этим числам, составят нужную выборку. Данный метод отбора учащихся непригоден при объеме генеральной совокупности больше тысячи учащихся в виду большой сложности в организации и финансового обеспечения усилий многих людей.

Стратифицированный отбор. В процессе исследования бывает необходимо учитывать некоторые качественные или количественные характеристики отдельных групп изучаемой совокупности. Например, требуется исследовать учащихся младших, средних и старших классов, а также учащихся с плохой, средней и хорошей успеваемостью, с учетом места жительства в городе или сельской местности. Во избежание увеличения объема выборки стратифицированный отбор предполагает обследование каждой из этих групп учащихся в отдельности с последующим объединением результатов обследования.

Стратификация есть деление генеральной совокупности на однородные по одному или нескольким признакам группы (страты). Если затем из каждой группы пропорционально ее объему отбирается нужное число объектов, то выборка будет качественно представительной для данной совокупности. Этот способ называется пропорциональным стратифицированным отбором.

Методика стратифицированного отбора включает в себя три этапа: 1) деление совокупности на типические группы (страты), 2) составление случайной выборки из каждой страты, 3) объединение статистических оценок, полученных по каждой выборке, в составную статистическую оценку, взвешенную пропорционально объему страт.

Систематический (систематизированный, интервальный) отбор. Метод систематического отбора заключается в том, что выборку из совокупности производят путем отбора объектов через фиксированный интервал, что можно применить при исследовании упорядоченных объектов (например, пачка тетрадей с контрольными работами), или переписанных объектов (список фамилий учащихся). Если известен объем совокупности (N) и объем выборки (n), величина интервала (k) устанавливается следующим образом:

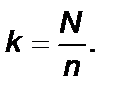
Величина интервала будет равна отношению N к n. Величина интервала может быть установлена произвольно, когда одно из этих чисел неизвестно.

Использование метода систематического отбора может привести к ошибочным выводам, если объекты совокупности расположены в циклическом порядке (например, в стопке тетрадей контрольные работы каждого класса сложены по оценкам: сначала отличные работы, затем хорошие, посредственные и неудовлетворительные). При совпадении величины интервала отбора с периодом цикла в выборку могут попасть объекты (например, посредственные работы), которые составят непредставительную выборку.

К неслучайным методам выборки относятся бессистемный отбор, доступная и целенаправленная выборка. Бессистемный отбор заключается в изучении объектов, случайно встретившихся исследователю. Доступная выборка составляется из объектов, изучение которых находится в возможностях исследователя, от предыдущего отличается систематизированностью. Целенаправленная выборка составляется в тех случаях, когда исследователь прибегает при отборе объектов измерения к помощи лица, хорошо знающего всех членов совокупности (например, учителя или директора).

В процессе педагогического исследования невозможно устранить влияние всех случайных или не подлежащих изучению факторов на конечные результаты. Очень большое множество как объективных, так и субъективных факторов оказывают воздействие в ходе эксперимента на те или иные стороны учебно-воспитательного процесса. Это влияние может быть ограничено, если при составлении выборки учащихся будут соблюдаться следующие условия: объем выборки устанавливается в зависимости от цели исследования и должен составлять достаточно большую часть объема той совокупности, которая подлежит изучению; объекты измерения (учащиеся, школы) должны быть максимально вариативны по состоянию измеряемого признака; объекты измерения должны быть максимально однородны по состоянию общих (не подлежащих изучению) признаков; выводы, полученные на основе изучения репрезентативной выборки, можно распространить на учащихся, не включенных в выборку, если они принадлежат к той же совокупности, из которой сделана выборка.

Основные понятия по теме

ВАРИАНТА [< лат. varians (variantis) – изменяющийся] – в статистике – каждый член ряда чисел.

ВАРИАНСА (дисперсия) – показатель разброса (дисперсии) данных, соответствующих среднему квадрату отклонений этих данных от средней арифметической; варианса равна стандартному отклонению, возведенному в квадрат.

ВЫБОРКА – это небольшое количество элементов, отобранных с помощью научных методов так, чтобы она была репрезентативной, то есть отражала популяцию в целом.

ГЕТЕРОГЕННОСТЬ (выборки) – свойство выборки, данные которой в значительной степени разбросаны на шкале распределения, что проявляется большим стандартным отклонением и свидетельствует о том, что данные сильно отличаются друг от друга.

ГИПОТЕЗА СТАТИСТИЧЕСКАЯ – утверждение, касающееся распределения популяции или различия между двумя популяциями, основанное на данных, полученных на выборках из этих популяций; существует в форме нулевой гипотезы и альтернативной гипотезы.

ГИПОТЕЗА НУЛЕВАЯ – гипотеза, согласно которой различия между выборками обусловлены только случайностью и не отражают действительных различий между популяциями, из которых взяты эти выборки. Обычно нулевая гипотеза выдвигается с целью ее опровержения в пользу альтернативной гипотезы.

ГИПОТЕЗА АЛЬТЕРНАТИВНАЯ – гипотеза, согласно которой различия между выборками являются значимыми, т.е. отражают соответствующее различие между популяциями, из которых взяты эти выборки. Обычно альтернативная гипотеза соответствует рабочей гипотезе исследователя.

ГЕНЕРАЛИЗАЦИЯ [< лат. generalis – общий, главный] – обобщение, логический переход от частного к общему; подчинение частных явлений общему принципу.

КРИВАЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ – колоколообразная кривая, обладающая симметрией относительно средней и характерная для популяции, подчиняющейся закону нормального распределения.

КРИВАЯ КОЛОКОЛООБРАЗНАЯ – кривая, характеризующая распределение большинства количественных данных или результатов. Такую кривую для уровней интеллекта можно получить, исследуя распределение результатов интеллектуального тестирования большой группы лиц. Из подобных кривых видно, что результаты большинства исследуемых группируются вокруг среднего уровня, а по мере удаления в ту или иную сторону от этого уровня число их становится все меньше. Именно это и обусловливает характерную колоколообразную форму кривой.

КРИТЕРИЙ СТАТИСТИЧЕСКИЙ – статистический показатель, позволяющий принять или отвергнуть ту или иную гипотезу в зависимости от вероятности того, что различия обусловлены чистой случайностью.

МЕДИАНА [< лат. mediana – средняя] в статистике – срединное или центральное значение.

МОДА [< лат. modus – мера, образ, способ, правило, предписание] в статистике – величина признака, измерение исследуемого явления, которым соответствует наибольшее число случаев или показаний и которым выражают наиболее часто встречающийся тип данного явления.

ОБОБЩЕНИЕ СТАТИСТИЧЕСКОЕ – изучение выводов, которые могут быть распространены на популяцию, исходя из данных, полученных на выборке, а также оценка степени достоверности таких выводов.

ОТКЛОНЕНИЕ СТАНДАРТНОЕ – показатель, характеризующий разброс в распределении относительно среднего.

ПОПУЛЯЦИЯ (в статистике) – совокупность всех элементов реальной или теоретической группы лиц, предметов и т.п.

РЕПРЕЗЕНТАТИВНОСТЬ [< фр. representatif – представительный; показательный] в статистике, в экспериментальных исследованиях – показательность каких-либо наблюдений; соответствие характеристик, полученных в результате частичного (выборочного) обследования какого-либо объекта, характеристикам этого объекта в целом, позволяющее распространить выводы частичного обследования на весь изучаемый объект.

СТАТИСТИКА [< нем. statistik < лат. status – состояние] – 1) вид практической деятельности, направленной на сбор, обработку, анализ и публикацию информации, характеризующей количественные закономерности жизни общества в связи с их количественным содержанием; 2) наука, излагающая общие вопросы сбора, измерения и анализа массовых количественных данных; 3) математическая статистика - раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов.

Вопросы и задания для самоконтроля

1. Каково значение методов сводки и обработки результатов в научном исследовании?

2. Раскройте основные этапы применения статистических методов.

3. В чём сущность главных разделов статистики: описательная статистика, индуктивная статистика, изменение корреляции?

4. В чём заключается проблема репрезентативности выборки в исследовании?