Приложение 2. измерение скорости дозвукового потока газа

При течении газа с существенно дозвуковой скоростью (М < 0,3) его плотность не зависит от скорости движения и это движение может быть описано уравнениями, полученными для несжимаемой жидкости. В этом случае скорость газа находится из уравнения Бернулли, записанного для двух сечений элементарной струйки, в которой происходит энергетически изолированное и изоэнтропийное торможение несжимаемого газа от скорости потока до нулевой скорости:

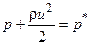
Разрешая это уравнение относительно скорости, получаем:

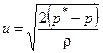(П.2.1)

Из уравнения (П.2.1) следует, что для определения скорости газа при М<0,3 необходимо измерить статическое и полное давления в одной и той же точке потока. При этом плотность газа считается известной.

Схема измерения полного и статического давлений представлена на рис. П.2.1. Полное давление измеряется с помощью трубки Пито 1, перед которой происходит энергетически изолированное и изоэнтропийное торможение газа. Статическое давление должно измеряться в той же точке потока, в которой измеряется полное давление. Но при дозвуковом течении статическое давление постоянно поперек потока и поэтому его можно измерить в любой точке сечения, проходящего через срез трубки Пито. Обычно это давление измеряется на обтекаемой стенке с помощью отборника статического давления 2, представляющего собой отверстие диаметром порядка 0,5 мм в стенке, вдоль которой движется поток. Ось отверстия должна быть перпендикулярна поверхности стенки.

С целью уменьшения погрешности определения скорости газа при использовании формулы (П.2.1) следует измерять не каждое из давлений р^* и р, а непосредственно разность давлений (р^* - р) с помощью дифференциального манометра. При величине (р^* - р), не превышающей 0,01…0,015 МПа можно использовать водяной U-образный дифманометр 3. В этом случае измеряется перепад уровней воды в дифманометре Dh_p в м вод.ст., которые переводятся в паскали следующим образом: (р^* - р) [Па] = 10⁴Dh_p [м вод.ст.]. Необходимая точность измерения разности давлений с помощью водяного дифманометра, изображенного на рис. П.2.1, обеспечивается только в том случае, если перепад уровней жидкости в этом дифманометре не менее 1 мм. Данный перепад соответствует при нормальных условиях скорости воздуха 4 м/с.

При меньшей скорости газа для измерения разности давлений необходимо использовать наклонный микроманометр, например типа ММН (поз. 4 на рис. П.2.1). Для повышения точности измерения малых разностей давлений в этом манометре в качестве рабочей жидкости используется этиловый спирт с плотностью r_сп = 809,5 кг/м³ и наклонная измерительная трубка 5. Разность давлений, измеряемая этим микроманометром, равна

p^* - p =r_спgDh_usina = 10³×gDh_uK (П.2.2)

В этом выражении: Dh_u – отклонение уровня жидкости от нулевой отметки в наклонной измерительной трубке, м, K – постоянная прибора (K = 10^-3×r_спsina). Значения K нанесены на шкале микроманометра.

Подстановка (П.2.2) в (П.2.1) при K = 0,2 дает:

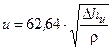[м/с] (П.2.3)

В формуле (П.2.3) r – плотность газа, которая рассчитывается по уравнению состояния

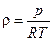[кг/м³]

Здесь: р – давление газа, Па; Т – температура газа, К; R – удельная газовая постоянная, Дж/(кг×К).

ЛИТЕРАТУРА

1. Абрамович Г.Н. Теория турбулентных струй. - М.: Физматгиз, 1960. - 715с.

2. Абрамович Г.Н. Прикладная газовая динамика. В 2 ч. Ч. 1. Учеб. руководство: Для втузов. – 5-е изд., перераб. и доп. – М.: Наука. Гл. ред. Физ.-мат. лит., 1991. – 600 с.

3. Абрамович Г.Н., Гиршович Т.А., Крашенинников С.Ю., Секундов А.Н., Смирнова И.П. Теория турбулентных струй. - М.: Наука, 1984. - 716 с.

4. Бетчелор Дж. Введение в динамику жидкости. М.: Мир, 1973. – 758 с.

5. Борисенко А.И. Газовая динамика двигателей. – М.: Оборонгиз, 1962. – 793 с.

6. Зуев В.С., Макарон В.С. Теория прямоточных и ракетно-прямоточных двигателей. М.: Машиностроение, 1971. – 368 с.

7. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1973. – 848 с.

8. Сергель О.С. Прикладная гидрогазодинамика. М.: Машинострое­ние, 1981 - 374с.

9. Степчков А.А. Прикладная гидрогазодинамика. Учеб. пособ. к лаб.раб. – М.: МАИ, 1980. – 58 с.

10. Хинце И.О. Турбулентность. Ее механизм и теория. - М.: Физматгиз, 1963. - 680 с.