Приложение 1. Модель турбулентности Прандтля

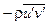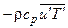Для расчета параметров пространственных турбулентных течений используются дифференциальные уравнения в частных производных, все члены которых осреднены по времени. В случае двумерного течения эти уравнения содержат члены и , которые можно рассматривать как дополнительное (кажущееся) турбулентное напряжение 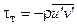и дополнительный поток тепла 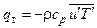. Осредненные по времени произведения пульсационных параметров жидкост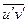и и 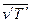называются моментами корреляции.

Чтобы получить замкнутую систему осредненных уравнений турбулентных течений, необходимо выразить моменты корреляции через осредненные параметры жидкости. Для этого используются модели турбулентности. Ограничимся рассмотрением одной из самых простых моделей турбулентности, которая называется моделью пути перемешивания (или смешения) Прандтля.

Рассмотрим плоское течение с направлением, одинаковым во всех точках пространства, и со скоростью, изменяющейся только при переходе от одной линии тока к другой. Направление главного течения пусть совпадает с осью х (рис. П.1.1).

Следовательно,

u=u(y), v=0, w=0.

Из дополнительных (кажущихся) турбулентных касательных напряжений в рассматриваемом случае имеется только касательное напряжение

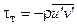(П.1.1)

Вследствие пульсаций давления в турбулентном потоке возникают области с повышенным и пониженным давлением. В областях с повышенным давлением формируются объемы жидкости (моли) которые движутся из этих областей в области с пониженным давлением.

Л.Прандтль предположил, что в слое с координатой у формируется моль, который движется вдоль оси у с положительной скоростью v', не взаимодействуя с окружающей жидкостью. При этом он переносит с собой х-составляющую количества движения, определяемую продольной проекцией скорости u(y). Пройдя расстояние l', моль разрушается, сливаясь с жидкостью в слое (y+l'). При этом в слое (y+l') возникает отрицательная пульсация скорости u'

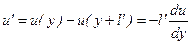(П.1.2)

Таким образом, моли жидкости, перемещающиеся из слоя у в слой (y+l') с положительным значением v', вызывают отрицательную пульсацию u'. И наоборот, моли, движущиеся из слоя (y+l') в слой у с отрицательной скоростью v' , вызывают положительную пульсацию u', т.е. знаки u' и v' противоположны.

Из опыта известно, что 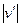~ 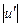. Следовательно, с учетом знаков u', v' и (П.1.2) можно записать

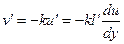
Произведение u'v' равно

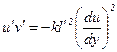
Проводя осреднение последнего выражения по времени и вводя обозначение 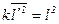, получаем

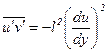(П.1.3)

Для того чтобы согласовать знак момента корреляции 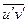со знаком производной du/dy в (П.1.3) это выражение записывают в виде

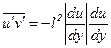(П.1.4)

Подстановка выражения (П.1.4) в (П.1.1) дает

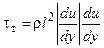
В случае двумерного течения, при котором u=u(x,y), в приведенных выше формулах полные производные заменяются на частные производные:

, .

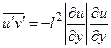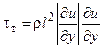Величина l называется путем перемешивания (или смешения) Прандтля.

Выражение для кажущегося турбулентного напряжения t_т можно записать по аналогии с напряжением молекулярного трения 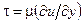, введя кажущуюся вязкость m_т

;

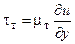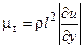
Аналогично дополнительный турбулентный поток тепла записывается в виде:

;

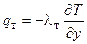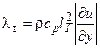
Здесь: l_т – коэффициент турбулентной теплопроводности, l_T – путь перемешивания для турбулентного переноса тепла.

Коэффициенты турбулентной вязкости и теплопроводности не зависят от природы жидкости, а определяются видом течения.