Описание экспериментальной установки

Изложение теории

Течения в каналах являются пространственными течениями и для определения всех их параметров необходимо решать систему дифференциальных уравнений в частных производных. Но для расчета изменения по длине канала давления и средней по сечению канала скорости можно использовать математическую модель, полученную для элементарной струйки, т.е. модель одномерного течения. Для того чтобы применить уравнения элементарной струйки к потокам реальной жидкости в каналах, необходимо учесть в этих уравнениях отличие кинетической энергии, рассчитанной по среднемассовой скорости от истинной кинетической энергии неравномерного потока. Это делается с помощью коэффициента Кориолиса a, равного отношению действительной кинетической энергии потока с неравномерным полем скоростей к кинетической энергии потока с тем же расходом, но имеющего равномерное поле скоростей в том же сечении канала. Значение коэффициента Кориолиса зависит от режима течения жидкости (числа Рейнольдса); для ламинарного режима a = 2, для турбулентного a = 1,1 [5].

С учетом изложенного при стационарном течении вязкой несжимаемой (r = const) жидкости в канале переменного сечения среднемассовая скорость и давление жидкости в любом сечении канала могут быть найдены из решения системы двух уравнений – уравнения неразрывности и уравнения энергии в механической форме (уравнения Бернулли), записанных для двух сечений канала – 1 и 2:

F₁W₁ = F₂W₂ (1.1)

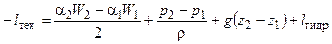(1.2)

В этих уравнениях: F – площадь поперечного сечения канала, W – среднемассовая скорость жидкости, r - ее плотность, p – давление, z – расстояние центра сечения канала от нивелирной плоскости, для которой z = 0, g – ускорение свободного падения, l_тех – техническая работа, l_гидр – работа, затраченная жидкостью на преодоление гидравлических сопротивлений, a - коэффициент Кориолиса.

Первый член правой части уравнения (1.2) описывает изменение кинетической энергии жидкости, второй – изменение потенциальной энергии давления и третий – изменение потенциальной энергии положения. В соответствии с уравнением Бернулли (1.2) техническая работа l_тех, подведенная к жидкости, идет на изменение ее кинетической энергии W²/2, потенциальной энергии давления р/r [совершение работы проталкивания (р₂-р₁)/r], потенциальной энергии положения gz и совершение работы по преодолению гидравлических сопротивлений l_гидр.

Последний член уравнения (1.2) учитывает гидравлические потери – уменьшение механической энергии жидкости вследствие трения о твердые поверхности и внутри жидкости. Гидравлические потери подразделяются на потери на трение и местные потери. Потери на трение связаны с движением вязкой жидкости вдоль твердых поверхностей, а местные потери – с образованием вихревых зон, возникающих при повороте потока, изменении площади канала и т.п.

Местные потери рассчитываются по формуле Вейсбаха [4]

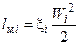(1.3)

Здесь: W_i – скорость в i-ом сечении канала, x_i – коэффициент местного сопротивления.

Потери на трение в канале круглого сечения длиной l и диаметром d определяются по формуле Дарси-Вейсбаха [4]

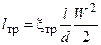(1.4)

В этой формуле: x_тр – коэффициент трения, W – средняя скорость жидкости на рассматриваемом участке канала (на его длине l).

Если поперечное сечение канала не является кругом, то в формулу (1.4) вместо диаметра d необходимо подставлять гидравлический диаметр d_г[4]:

.

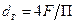Здесь: F – площадь поперечного сечения канала, П – его периметр.

Коэффициент трения зависит от числа Рейнольдса (режима течения) и относительной шероховатости стенок трубы:

x_тр = f(Re, D/r)

Здесь: Re – число Рейнольдса, D - средняя высота гребешков шероховатости, r – радиус (гидравлический радиус) канала.

Число Рейнольдса рассчитывается по формуле:

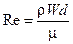
в которой: r, W и m - плотность, скорость и динамический коэффициент вязкости, d – диаметр (гидравлический диаметр) канала.

Для ламинарного режима течения жидкости в трубе (Re < 2300) [1, 4]

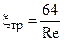
В этом случае

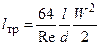~ W,

т.е. при ламинарном течении потери на трение пропорциональны скорости течения в первой степени.

При турбулентном режиме течения в трубе с гидравлически гладкой поверхностью стенок коэффициент трения рассчитывается по формуле Блазиуса [1, 4]

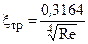2300 < Re < 10⁵

или по формуле Конакова [4]

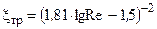Re > 10⁵

При больших значениях числа Рейнольдса (Re > 10⁵) коэффициент трения слабо зависит от Re; в этом случае потери на трение пропорциональны квадрату скорости жидкости и определяются только величиной относительной шероховатости стенок канала (рис. 1.1).

Из уравнения (1.1) следует, что при течении несжимаемой жидкости по каналу с постоянной площадью поперечного сечения (F₁ = F₂) W₁ = W₂, т.е. в этом случае скорость по всей длине канала остается постоянной: W = const. Если режим течения в канале не меняется, то a₁ = a₂ и первый член в правой части уравнения (1.2) обращается в нуль.

При течении несжимаемой жидкости по горизонтальному каналу (z₁=z₂) и отсутствии технической работы между рассматриваемыми сечениями (l_тех=0) уравнение (1.2) принимает вид:

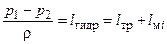[Дж/кг] (1.5)

В этом случае гидравлические потери на участке канала равны по абсолютной величине работе проталкивания или изменению потенциальной энергии давления на этом участке, т.е гидравлические сопротивления преодолеваются несжимаемой жидкостью за счет уменьшения потенциальной энергии давления этой жидкости при неизменном значении ее кинетической энергии.

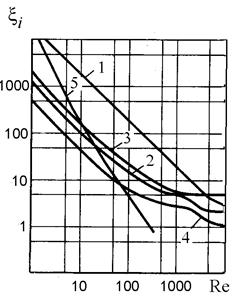
Местные потери определяются по формуле (1.3). При этом необходимо знать коэффициент местного сопротивления x_i. В первом приближении для типовых элементов трубопроводов (крана, фильтра и т.п.) значение этого коэффициента может быть определено по справочнику [3]. Зависимость коэффициента местного сопротивления некоторых элементов трубопроводов от числа Рейнольдса приведена на рис. 1.2.

В том случае, если местное сопротивление не является типовым или необходимо знать величину потерь с большей точностью, значение коэффициента местного сопротивления можно определить экспериментально. При этом используется уравнение (1.5), которое с учетом (1.4) принимает вид:

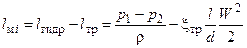[Дж/кг] (1.6)

В соответствии с формулой (1.3)

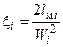(1.7)

Для того чтобы определить местные потери на каком-либо элементе трубопровода необходимо измерить разность давлений в двух сечениях трубопровода (перед и за местным сопротивлением) и скорость жидкости в трубопроводе. Вычитая из суммарных гидравлических потерь потери на трение на прямолинейном участке трубопровода, можно по формуле (1.6) определить l_мi.

Наряду с коэффициентом местных потерь для количественной оценки этих потерь в трубопроводах используют эквивалентную длину трубопровода l_экв. Это длина трубопровода, потери на трение по длине которого при той же скорости и диаметре равны потерям на местном сопротивлении, т.е.

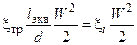
Отсюда

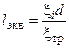
1.2. Лабораторная работа "Определение гидравлического сопротивления крана"

Цели работы - определение местного гидравлического сопротивления крана, коэффициента сопротивления крана, эквивалентной длины трубопровода, зависимости этих величин от числа Рейнольдса.

Описание экспериментальной установки

Эксперимент проводится на аэродинамической трубе, схема которой приведена на рис. 1.3.

Труба 1 изготовлена из прозрачного материала с гидравлически гладкой поверхностью и имеет квадратное поперечное сечение размером 100´100 мм. В центре трубы установлена модель крана 2. Установка работает на расширении воздуха, засасываемого из помещения вентилятором 3. Для обеспечения равномерного поля скоростей в мерном сечении 1 входной канал 4 в трубу спрофилирован по формуле Витошинского [2]. Наряду с обеспечением равномерного поперечного поля скоростей в трубе этот канал позволяет ускорять поток с минимальными потерями полного давления, т.е. можно принять, что полное давление в сечении 1 трубы р₁^* примерно равно атмосферному давлению В₀: р₁^* @ В₀. С помощью приемников статического давления 5 и 6, расположенных в сечениях 1 и 2, измеряется разность давлений (р₁–р₂). Эта разность давлений регистрируется в виде перепадов уровней воды Dh_p в двух вертикальных трубках батарейного манометра 7. Скорость воздуха в трубе определяется по разности полного и статического давлений (р₁^*-р₁), измеряемых в сечении 1 трубы. Полное давление р₁^* измеряется с помощью трубки Пито 8, а статическое давление – с помощью приемника статического давления 5. Разность давлений (р₁^*-р₁) регистрируется микроманометром 9, камера которого соединена с трубкой Пито 8, а наклонная трубка – с приемником статического давления 5. Измеряемая разность давлений (р₁^*-р₁) пропорциональна отклонению уровня спирта Dh_w в наклонной трубке микроманометра от нулевой отметки.

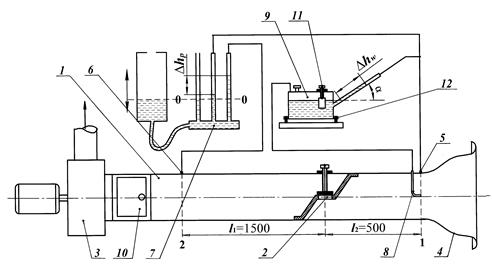
Рис. 1.3. Схема экспериментальной установки:

1 – аэродинамическая труба, 2 – модель крана, 3 – вентилятор, 4 – профилированный входной канал, 5 и 6 – приемники статического давления, 7 – водяной батарейный манометр, 8 – трубка Пито, 9 – наклонный микроманометр, 10 – окна перепуска, 11 – регулировочный винт установки уровня жидкости в наклонной трубке в нулевое положение, 12 – регулировочные винты установки микроманометра в горизонтальное положение

Так как скорость воздуха в трубе существенно дозвуковая (М<<0,3), то для расчета этой скорости используется формула (П.2.3), полученная для несжимаемой жидкости (см. Приложение 2):

.

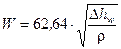При этом плотность воздуха в трубе r принимается равной плотности заторможенного потока r^*:

.

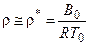Данная формула записана в предположении, что r = const, p₁^* @ B₀ и Т₁^* = Т₀ (B₀ и Т₀ – атмосферное давление и температура воздуха в помещении, в котором располагается экспериментальная установка).

Труба снабжена окнами перепуска 10, открывая которые можно изменять расход, а, следовательно, и скорость воздуха внутри трубы.