Косые скачки уплотнения

Изложение теории

Картина обтекания одного и того же тела дозвуковым и сверхзвуковым потоками качественно различна. При обтекании тела дозвуковым потоком элементарные волны давления, возникающие при взаимодействии потока с телом, распространяются во все стороны со скоростью звука. Эти волны уже на достаточном расстоянии искривляют линии тока, подготавливая поток для плавного обтекания тела. При обтекании затупленного тела сверхзвуковым потоком элементарные волны давления не могут распространяться против сверхзвукового потока и "подготавливать" его для плавного обтекания. Поэтому сверхзвуковой поток "натыкается" на препятствие так, что на некотором расстоянии от тела образуется скачок уплотнения, на котором ударно тормозится сверхзвуковой поток. Скачок уплотнения представляет собой сильную волну сжатия малой толщины (порядка длины свободного пробега молекул), в которой все параметры газа изменяются на конечную величину. Наличие скачкообразного изменения параметров газа на участке, имеющем малую протяженность (порядка длины свободного пробега молекул) указывает на то, что здесь имеет место внутренний молекулярный перенос, связанный с переходом кинетической энергии упорядоченного течения газа в кинетическую энергию беспорядочного теплового движения молекул. В результате этого происходит разогрев газа при прохождении его из невозмущенной области перед фронтом скачка уплотнения в область возмущенного движения за фронтом скачка уплотнения. Повышение средней квадратичной скорости движения молекул вызывает также возрастание давления и плотности невозмущенного газа при прохождении его через фронт скачка уплотнения.

При составлении математической модели течения газа через скачок уплотнения принимается, что газ является идеальным, а скачок уплотнения в связи с его малой толщиной рассматривается как геометрическая поверхность. Поверхность скачка является поверхностью сильного разрыва параметров газа – на ней все параметры газа и их производные терпят разрыв. В случае скачка уплотнения поверхность разрыва является нормальной, так как она перпендикулярна вектору скорости или его нормальной составляющей.

Скачки уплотнения могут быть прямыми или косыми. Прямыми скачками уплотнения называются скачки, фронт которых перпендикулярен вектору скорости набегающего потока. Косыми скачками уплотнения называются скачки, фронт которых составляет с вектором скорости набегающего потока угол a, отличный от прямого. Этот угол может меняться от угла характеристики a₀ до 90°. Косые скачки уплотнения возникают при повороте сверхзвукового потока, например при сверхзвуковом обтекании клина.

На рис. 2.1 показана фотография обтекания клина, полученная теневым методом. Ось клина совпадает с направлением вектора скорости невозмущенного потока. В этом случае на вершине клина образуются два косых скачка уплотнения, симметричных относительно оси симметрии клина.

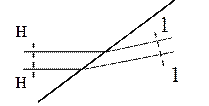
Задача обтекания клина сверхзвуковым потоком сводится к задаче обтекания этим потоком внутреннего тупого угла (180°- w), изображенного на рис. 2.2. На косом скачке уплотнения сверхзвуковой поток поворачивает на угол w: если первоначально газ двигался параллельно поверхности АВ, то после поворота он будет двигаться параллельно поверхности ВС. Параметры потока перед скачком уплотнения обозначим индексом н, а за скачком – индексом 1. До скачка уплотнения вектор скорости 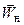составляет с фронтом скачка угол a, а за скачком вектор скорости 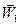составляет с фронтом скачка угол b. Из рисунка следует, что

a=w+b (2.1)

Разложим векторы скорости газа до скачка 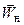и за скачком на составляющие, нормальные и тангенциальные к фронту скачка: W_нn, W_нt и W_1n, W_1t.

При пересечении косого скачка уплотнения газом нормальная составляющая его вектора скорости скачкообразно уменьшается на конечную величину (W_1n<W_нn), а тангенциальная оcтается неизменной (W_1t=W_нt=W_t). Для того, чтобы доказать это рассмотрим рис. 2.3, на котором изображен косой скачок уплотнения и контрольный объем н-1-1-н. Боковые поверхности н-1 этого объема перпендикулярны, а торцевые поверхности н-н и 1-1 параллельны фронту скачка. При этом площади поверхностей н-н и 1-1 равны: F_н = F₁. Так как давления на обеих боковых поверхностях н-1 одинаковы, то из уравнения количества движения, записанного в проекции на направление фронта скачка следует, что тангенциальная составляющая скорости W_t остается неизменной, откуда и вытекает условие W_1t=W_нt=W_t. Уравнение количества движения в проекции на нормаль к скачку с учетом равенства площадей F_н и F₁ (F_н=F₁=F)записывается следующим образом

F(p_н – р₁) = G(W_1n – W_нn)

В этом уравнении G – расход газа через поверхность н-н (или 1-1). Так как р₁> p_н, то W_1n< W_нn.

В связи с тем, что при пересечении косого скачка нормальная составляющая скорости газа W_n уменьшается, а тангенциальная составляющая W_t остается неизменной, косой скачок уплотнения можно представить как прямой скачок для нормальной составляющей скорости, сносимый вдоль фронта косого скачка со скоростью W_t.

В теории косых скачков уплотнения вводятся дополнительно три параметра течения: температура частичного торможения Т_n, условная критическая скорость звука a_крn и приведенная скорость l_n.

Температура частичного торможения - температура, которую принимает газ при энергетически изолированном погашении до нуля только нормальной составляющей скорости. Эта температура рассчитывается по формуле:

Т_n^*=Т+W_n²/2c_p

в которой: T - статическая температура газа, c_p – удельная теплоемкость газа при постоянном давлении.

Условная критическая скорость звука – критическая скорость звука, рассчитанная по формуле

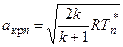
Приведенная скорость l_n – отношение нормальной составляющей скорости к условной критической скорости звука:

l_n=W_n/a_кpn

Получим формулы, связывающие параметры газа перед и за косым скачком уплотнения.

Течение в косом скачке уплотнения, также как и течение в прямом скачке уплотнения является энергетически изолированным (l_тех = 0 и q_н= 0) и поэтому из уравнения энергии в тепловой форме, записанного для элементарной струйки, пересекающей скачок (рис. 2.4), q_н - l_тех= i₁^* - i_н^* = с_р(Т₁^* - Т_н^*) следует i₁^* = i_н^* , Т₁^* = Т_н^* . Т.е. полная энергия газа, равная полной энтальпии (энтальпии торможения) газа, на косом скачке уплотнения не изменяется. Так как 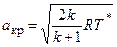и Т₁^* = Т_н^*, то а_кр1 = а_кр.н= а_кр.

Можно показать, что температура частичного торможения Т_n^*, также как и температура торможения Т^*, на косом скачке остается постоянной.

По определению Т_n^*=Т+W_n²/2c_p. Так как W² = W_n² +W_t², то

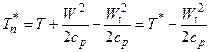
или для сечений н-н и 1-1 элементарной струйки, пересекающей скачок (рис. 2.4):

,

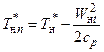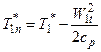
На косом скачке уплотнения Т₁^* = Т_н^* и W_1t = W_нt, следовательно Т_1n^* = Т_нn^*. Из этого равенства следует, что a_кр1n= a_кр.нn= a_крn.

Приведенные скорости l_нn и l_1n не являются нормальными составляющими приведенных скоростей l_ни l₁. Покажем это на примере приведенной скорости l_нn. Из рис. 2.2 следует, что W_нn = W_н×sina. Для того, чтобы в этом уравнении перейти к приведенным скоростям, необходимо левую часть разделить на a_кр.нn, а правую - на a_кр.н. Так как a_кр.нn ¹ a_кр.н, то l_нn¹l_н×sina. Таким же образом можно доказать, что l_1n¹l₁×sinb.

В отличие от приведенной скорости l_n число Маха М_n является нормальной составляющей М как перед, так и за скачком уплотнения

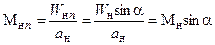(2.2а) 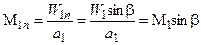(2.2б)

Так как косые скачки уплотнения являются прямыми скачками уплотнения для нормальных составляющих вектора скорости, то эти скачки можно рассчитывать по формулам, полученным для прямых скачков уплотнения с заменой l_ни l₁на l_нn и l_1n. Выполнив эту замену, получим следующие формулы, связывающие параметры течения за скачком с параметрами течения перед скачком:

- основное кинематическое соотношение

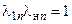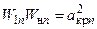или (2.3)

- уменьшение полного давления газа

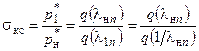(2.4)

- увеличение плотности газа

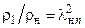(2.5)

- увеличение статического давления газа

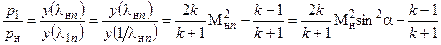(2.6)

- увеличение статической температуры

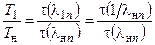(2.7)

Уравнение ударной адиабаты, состоящее из скалярных параметров, сохраняет ту же форму, что и для прямого скачка

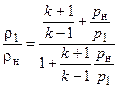
Часто при решении задач необходимо знать величину приведенной скорости за косым скачком уплотнения l₁. Связь между l₁ и l_нможно найти из треугольников скоростей за и перед скачком уплотнения (рис. 2.2):

W_1t = W₁ cosb = W_нt = W_н cosa

Отсюда

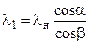
Из этих треугольников скоростей также можно получить уравнение, связывающее углы a, b и приведенную скорость l_нn. Разделив почленно W_нn = W_нttga на W_1n = W_1ttgb с учетом W_нt= W_1t, имеем:

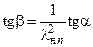(2.8)

Формулы (2.3)-(2.7) позволяют проводить как расчет, так и анализ изменения параметров газа при пересечении им косого скачка уплотнения.

Из формулы (2.3) следует, что за косым скачком уплотнения всегда l_1n < 1 и W_1n < a_крn, так как l_нn > 1 и W_нn > a_крn. Но скорость W₁ за косым скачком может быть как дозвуковой, так и сверхзвуковой. Так как при увеличении l значение газодинамической функции t(l) уменьшается, значение у(l) увеличивается и при l > 1 значение q(l) уменьшается, то t(l_нn)<t(l_1n), y(l_нn)>y(l_1n) и q(l_нn)<q(l_1n). В соответствии с формулами (2.4), (2.6) и (2.7) s_кс = р₁^*/ р_н^* < 1, p₁/p_н >1 и Т₁/Т_н >1. Из формулы (2.5) следует, что r₁/r_н >1. Это означает, что в косом скачке уплотнения (также как и в прямом, но в меньшей степени) полное давление уменьшается, а статическое давление и статическая температура увеличиваются. Качественное изменение параметров газа при пересечении им косого скачка уплотнения показано на рис. 2.2.

Приведенный формальный анализ изменения параметров газа при пересечении им скачка уплотнения полностью соответствует физической картине течения. Действительно, течение газа, пересекающего скачок уплотнения, является энергетически изолированным. Это означает, что полная энергия газа, равная полной энтальпии, остается постоянной. Полная энергия газа складывается из его тепловой энергии, потенциальной энергии давления и кинетической энергии (потенциальная энергия положения в случае газовых течений мала по сравнению с перечисленными видами энергии и ей можно пренебречь). Как было отмечено выше, при пересечении скачка уплотнения газом происходит увеличение его температуры и давления, что приводит к увеличению тепловой энергии и потенциальной энергии давления газа. В результате этого при постоянной полной энергии газа уменьшается кинетическая энергия и, соответственно, скорость газа. Уменьшение скорости газа при пересечении им скачка уплотнения следует и из уравнения обращения воздействий

,

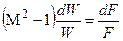в соответствии с которым при уменьшении площади сечения элементарной струйки сверхзвукового потока (рис. 2.4) скорость этого потока должна уменьшаться.

В соответствии с формулой (2.4) полное давление газа при пересечении им скачка уплотнения уменьшается. Это позволяет сделать вывод о том, что прохождение идеального газа сквозь скачок уплотнения не является изоэнтропическим процессом, а сопровождается необратимым переходом механической энергии в тепло.

На практике расчет косого скачка уплотнения сводится к определению параметров газа за скачком уплотнения по заданным значениям угла w, числа Маха М_н и известным параметрам газа перед скачком уплотнения с использованием формул (2.4)-(2.7).

Для того, чтобы воспользоваться этими формулами, необходимо знать приведенную скорость l_нn, которую можно определить по нормальной составляющей числа Маха перед скачком уплотнения 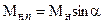. Связь между l_нn иМ_нn устанавливается формулой [1, 4]

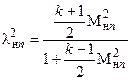(2.9)

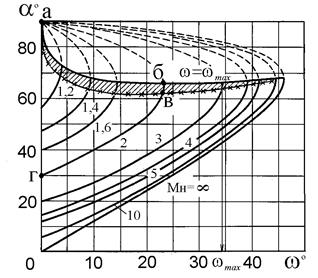При проведении расчетов значение l_нn удобнее находить по значению М_нn из таблиц газодинамических функций, не обращая внимания на индекс n. Заменив l_нn наМ_нn, мы заменили одно неизвестное на другое, так как для вычисления М_нn необходимо знать угол a. Этот угол можно найти по графикам a=f(М_н,w), построенным в результате решения системы уравнений (2.1), (2.2а), (2.8) и (2.9). Зависимость a=f(М_н,w) для газа с показателем адиабаты k = 1,4 (воздуха) графически представлена на рис. 2.5.

Точки пересечения кривых М_н= const с прямой w = 0 (точки г) соответствуют характеристикам сжатия, для которых 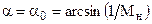. Участки кривых г-в соответствуют косым скачкам уплотнения, за которыми поток остается сверхзвуковым (М₁ > 1). Такие скачки называются слабыми косыми скачками. Участки кривых в-а соответствуют так называемым сильным косым скачкам, за которыми скорость потока становится дозвуковой (М₁ < 1). Опыт показывает, что в обычных условиях сильные косые скачки, соответствующие участкам кривых б-а, не реализуются, так как они являются неустойчивыми. Из рисунка видно, что прямая w = const пересекает кривые М_н = const в двух точках, т.е. одному значению w при заданном М_н могут соответствовать два значения угла a. Из приведенного выше следует, что из этих углов a необходимо выбирать меньшее значение, при котором реализуется устойчивый косой скачок уплотнения. Кроме этого из рис. 2.5 следует, что для заданного значения числа М_н существует максимальный угол отклонения потока в косом скачке уплотнения w_max. Если w > w_max, то поворот потока в косом скачке уплотнения не возможен и перед телом возникает отошедшая (отсоединенная) ударная волна, в которой угол a меняется от 90° до a₀.

2.2. Лабораторная работа "Теоретическое и экспериментальное исследование косых скачков уплотнения"

Цель работы - теоретическое и экспериментальное исследование изменения параметров газа на косом скачке уплотнения. После обработки экспериментальных данных и проведения теоретических расчетов должны быть получены зависимости a=f₁(w), s=f₂(a) и р₁/р_н=f₃(a), которые представляются в виде графиков, позволяющих сравнить результаты расчета и эксперимента.