Построение диаграммы суммарной поршневой силы
Масштабы длин и сил на диаграмме суммарной поршневой силы принимаем такими же, как и на индикаторной диаграмме. По оси абсцисс откладываем двойной ход, по оси ординат – силы П, Iп, Rп (рис. 3.10).
Графическое перестроение индикаторной диаграммы сил от давления пара на поршень рFп = f(s) в развернутую диаграмму сил по углу поворота вала рFп = f(α) производим по методу Брикса. Под диаграммой суммарной поршневой силы проводим две полуокружности диаметром, равным ходу поршня. Из центров полуокружностей к середине диаграммы в принятом масштабе откладываем отрезки длиной ∆ = λr/2, где λ = r/lш = 0,038/0,18 = = 0,211; ∆ = 0,211·0,038/2 = 0,00401 м.

Рис. 3.10. Диаграмма суммарной свободной силы
Из точки ОI через угол 15º проводим линии до пересечения с полуокружностями. Проекции точек пересечения линий с полуокружностями на ось абсцисс показывают перемещение поршня, соответствующее повороту вала на угол α. Левая часть диаграммы соответствует ходу поршня к валу (α = 0 ÷ 180), правая – обратному ходу (α = 180 ÷ 360).
Силы от давления пара на поршень, взятые из индикаторной диаграммы, силы инерции и силы трения откладываем на вертикальных линиях диаграммы в соответствии с углом поворота кривошипа α. Для расчета сил инерции первого и второго порядка определим угловую скорость вала компрессора и массу поступательно движущихся частей: ω = 2πn; ω = 2·3,14·24 = 151 рад/с:
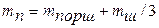 ,
,
где mпорш = 0,5 кг – масса поршня в сборе с поршневым кольцом, уплотнительными и маслосъемными кольцами; mш = 1,1 кг – масса шатуна.
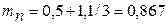 кг.
кг.
Результаты расчета сил инерции в зависимости от поворота угла α приведены в табл. 3.7.
Сила трения для одного цилиндра Rп1 = Rп/z = 0,65Nтр/сmz = 0,65·3,3·103/3,65·8 = 73,7 Н, где Nтр и сm взяты из теплового расчета. Сумма ординат всех сил для каждого угла поворота соответствует значениям суммарной силы. Из диаграммы видно, что наибольшие значения силы Р, а следовательно, и сжимающей шатун силы Рш действуют в момент, когда поршень приближается к верхней мертвой точке.
Таблица 3.7.
Результаты расчета сил инерции
| α | λcos2α | In2, Н | In2, Н | In, Н |
| 0,2111 | – 751 | – 159 | – 910 | |
| 0,182818 | – 726 | – 137 | – 863 | |
| 0,10555 | – 651 | – 79 | – 730 | |
| – 531 | – 531 | |||
| – 0,10555 | – 376 | – 296 | ||
| – 0,18282 | – 194 | – 57 | ||
| – 0,2111 | ||||
| – 0,18282 | ||||
| – 0,10555 | ||||
| 0,10555 | – 79 | |||
| 0,182818 | – 137 | |||
| 0,2111 | – 159 | |||
| 0,182818 | – 137 | |||
| 0,10555 | – 79 | |||
| – 0,10555 | ||||
| – 0,18282 | ||||
| – 0,2111 | ||||
| – 0,18282 | – 194 | – 57 | ||
| – 0,10555 | – 376 | – 296 | ||
| – 531 | – 531 | |||
| 0,10555 | – 651 | – 79 | – 730 | |
| 0,182818 | – 726 | – 137 | – 863 | |
| 0,2111 | – 751 | – 159 | – 910 |
Значения газовой и суммарной сил в зависимости от угла поворота α приведены в табл. 3.8.
Построение диаграммы суммарной тангенциальной силы
Тангенциальную силу для одного цилиндра (табл. 3.9) рассчитываем на основе полученных выше значений суммарной свободной силы для 24 положений кривошипа. Значения функции sin(α+β)/cosβ могут быть определены с помощью уравнений
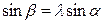
и
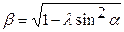
Таблица 3.8.
Результаты расчета суммарной поршневой силы
| Α | Rтр, Н | Iп, H | Pг, Н | P, Н | |||||
| – 74 | – 910 | ||||||||
| – 74 | – 863 | ||||||||
| – 74 | – 730 | ||||||||
| – 74 | – 531 | ||||||||
| – 74 | – 296 | ||||||||
| – 74 | – 57 | – 71 | |||||||
| – 74 | – 92 | – 7 | |||||||
| – 74 | – 92 | ||||||||
| – 74 | – 92 | ||||||||
| – 74 | – 92 | ||||||||
| – 74 | – 92 | ||||||||
| – 74 | – 92 | ||||||||
| – 74 | – 92 | ||||||||
| – 57 | |||||||||
| – 296 | |||||||||
| – 531 | |||||||||
| – 730 | |||||||||
| – 863 | |||||||||
| – 910 |
В координатах Рt, α строится кривая тангенциальных сил для одного цилиндра. Затем, последовательно смещая по углу поворота кривошипа кривую тангенциальных сил одного цилиндра на угол развала между рядами компрессора, равный 45°, строятся кривые тангенциальных сил для всех цилиндров. Кривая суммарной тангенциальной силы получается сложением ординат всех кривых тангенциальных сил.
Тангенциальная сила трения вращающихся частей Rвр компрессора принимается постоянной. Ее влияние учитывается смещением начала отчета ординат суммарной кривой тангенциальных сил от оси абсцисс на отрезок равный в масштабе сил диаграммы. Среднее значение суммарной тангенциальной силы определяется планиметрированием площади под кривой ∑Рt + Rвр. Частное от деления полученной площади на длину диаграммы (0 – 360°) дает ординату Рtср.
Кривая суммарных тангенциальных сил в соответствующем масштабе является кривой моментов, противодействующих вращению вала (рис. 3.11):
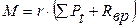 .
.
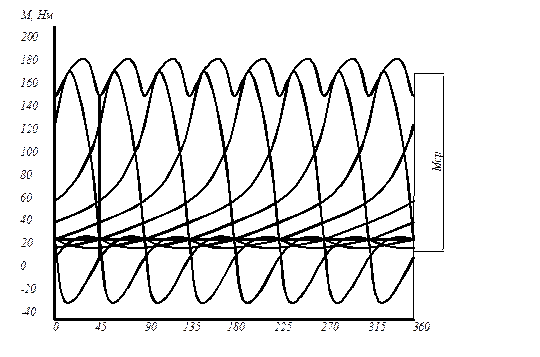
Рис. 3.11. Диаграмма суммарного противодействующего момента
Площадки над прямой Мср принято считать положительными, под прямой – отрицательными. При точном определении Мср алгебраическая сумма всех площадок должна равняться нулю. По наибольшей площади рассчитывается маховик.
Результаты расчета тангенциальных сил и противодействущего момента в зависимости от поворота угла α приведены в табл. 3.9.
Момент, действующий от силы Rвр: Мвр = 316·0,038 = 12 Нм, тогда момент, противодействующий вращению вала, будет равен:
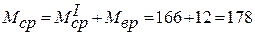 Нм,
Нм,
где МIср – среднее значение суммарного момента от сил Pt, определенное путем планиметрирования площади под кривой Мкр∑,.
Мощность на валу компрессора по диаграмме противодействующего момента:
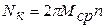 ;
; 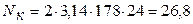 кВт
кВт
Из теплового расчета Nк = 25,6 кВт, следовательно, графические построения выполнены достаточно точно.
Таблица 3.9.
Результаты расчета тангенциальных сил и противодействующего момента
| α | 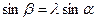
| 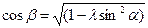
| 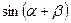
| P, Н | P, Н | Pt, Н | Mкр, Нм | МкрΣ, Нм |
| 0,0578 | 0,9925 | 0,3127 | -1669 | -63 | ||||
| 0,1118 | 0,9717 | 0,5826 | -1191 | -45 | ||||
| 0,1580 | 0,9425 | 0,7782 | -482 | -18 | ||||
| 0,1936 | 0,9123 | 0,8869 | -68 | -3 | ||||
| 0,2159 | 0,8896 | 0,9152 | -71 | -73 | ||||
| 0,2235 | 0,8812 | 0,8812 | -7 | -2 | ||||
| 0,2159 | 0,8896 | 0,8035 | -157 | -6 | ||||
| 0,1936 | 0,9123 | 0,6933 | -223 | -8 | ||||
| 0,1580 | 0,9425 | 0,5547 | -215 | -8 | ||||
| 0,1118 | 0,9717 | 0,3891 | -160 | -6 | ||||
| 0,0578 | 0,9925 | 0,2010 | -84 | -3 | ||||
| -0,0578 | 0,9925 | -0,2010 | ||||||
| -0,1118 | 0,9717 | -0,3891 | ||||||
| -0,1580 | 0,9425 | -0,5547 | ||||||
| -0,1936 | 0,9123 | -0,6933 | ||||||
| -0,2159 | 0,8896 | -0,8035 | ||||||
| -0,2235 | 0,8812 | -0,8812 | ||||||
| -0,2159 | 0,8896 | -0,9152 | ||||||
| -0,1936 | 0,9123 | -0,8869 | ||||||
| -0,1580 | 0,9425 | -0,7782 | ||||||
| -0,1118 | 0,9717 | -0,5826 | ||||||
| -0,0578 | 0,9925 | -0,3127 | ||||||
Построение диаграммы радиальных сил
Диаграмма радиальных сил строится в координатах Pr, α (рис. 3.12). Необходимые для расчета радиальной силы значения функции cos(α+β)/cosβ = f(λ;α) приведены в работе [3]. Значения радиальной силы в зависимости от угла поворота кривошипа, полученные в ходе расчета, приведены в таблице 3.10.
В радиальном направлении на кривошип кроме силы Pr, действуют постоянные по величине силы инерции Iш.ш от массы части шатунной шейки, приходящейся на один шатун, и от вращающейся части шатуна Iш.вр: Iш.ш. = mIш.шrω2, где mIш.ш = πd2ш.ш lш.шρ/(4i) – масса шатунной шейки, приходящейся на один шатун; i – число шатунов на одной шейке; ρ – плотность материала коленчатого вала.
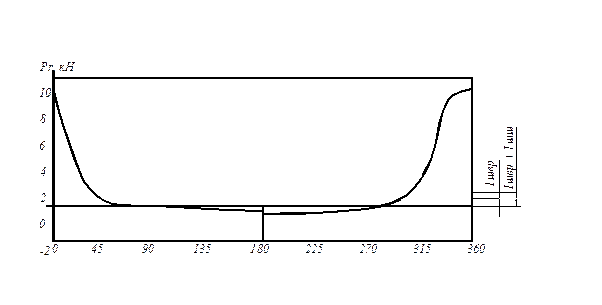
Рис. 3.12. Диаграмма радиальных сил
После подстановки получим
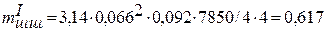 кг;
кг;
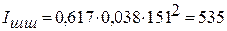 Н;
Н;
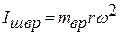 ,
,
где mвр = 2/3mш – масса вращающейся части шатуна.
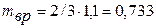 кг;
кг;
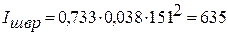 Н.
Н.
Результирующая сила, действующая на шатунный подшипник:
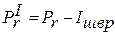 .
.
Результирующая сила, действующая на вал компрессора:
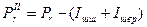 .
.
Результаты расчетов результирующих радиальных сил приведены в табл. 3.10.
Таблица 3.10.
Результаты расчета радиальных сил
| α | cos(α + β)/cosβ | Р | Рr | РIr | РIIr |
| 0,9518 | |||||
| 0,8132 | |||||
| 0,6009 | – 284 | – 819 | |||
| 0,3398 | – 611 | – 1146 | |||
| 0,0588 | – 73 | – 4 | – 639 | – 1174 | |
| – 0,2148 | – 635 | – 1170 | |||
| – 0,4588 | – 80 | – 715 | – 1250 | ||
| – 0,6601 | – 194 | – 829 | – 1364 | ||
| – 0,8134 | – 297 | – 932 | – 1467 | ||
| – 0,9189 | – 368 | – 1003 | – 1538 | ||
| – 0,98 | – 406 | – 1041 | – 1576 | ||
| – 1 | – 417 | – 1052 | – 1587 | ||
| – 1 | – 657 | – 1292 | – 1827 | ||
| – 0,98 | – 661 | – 1296 | – 1831 | ||
| – 0,9189 | – 658 | – 1293 | – 1828 | ||
| – 0,8134 | – 615 | – 1250 | – 1785 | ||
| – 0,6601 | – 523 | – 1158 | – 1693 | ||
| – 0,4588 | – 395 | – 1030 | – 1565 | ||
| – 0,2148 | – 217 | – 852 | – 1387 | ||
| 0,0588 | – 558 | – 1093 | |||
| 0,3398 | – 485 | ||||
| 0,6009 | |||||
| 0,8132 | |||||
| 0,9518 | |||||
Уравновешивание
При проектировании компрессоров путем выбора схем расположения кривошипов коленчатого вала и цилиндров, подбора противовесов стремятся обеспечить условия, при которых суммарные силы инерции ∑Iп1; ∑Iп2; ∑Iвр, а также моменты этих сил ∑Мп1; ∑Мп2; ∑Мвр были бы равны нулю. С учетом сил инерции высоких порядков ввиду необходимости значительного усложнения конструкции полное уравновешивание практически неосуществимо.
При равенстве mп в рядах уравновешивание сил инерции и их моментов для компоновки проектируемого компрессора (рис. 3.13) будет следующим [3]: силы инерции первого порядка и силы инерции неуравновешенных вращающихся масс взаимно уравновешены за счёт симметричного расположения колен вала. Силы инерции второго порядка не уравновешиваются. Моменты от действия этих сил уравновешиваются следующим образом.

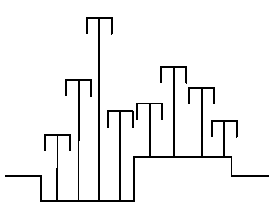
Рис. 3.13. Компоновка компрессора
Момент от действия сил инерции первого порядка:
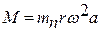 ;
; 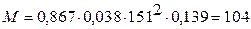 Нм.
Нм.
Он может быть уравновешен двумя противовесами с массой приведенной к радиусу кривошипа (рис. 3.14):
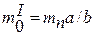 ;
; 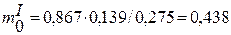 кг.
кг.
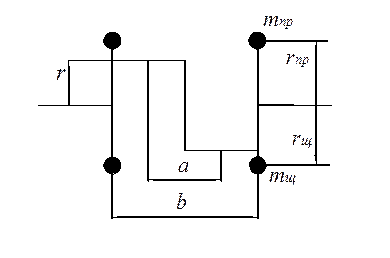
Рис. 3.14. Уравновешивание вращающихся масс
Момент сил инерции второго порядка равен нулю.
Момент сил инерции неуравновешенных вращающихся масс:
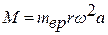 ,
,
где mвр – неуравновешенная вращающаяся масса, приведенная к радиусу кривошипа.
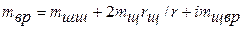 ,
,
где rщ – радиус инерции щеки (рис. 3.15); rщ = 0,052 м; mщ – масса неуравновешенной части щеки.
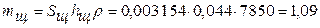 кг.
кг.
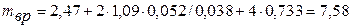 кг.
кг.
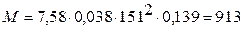 Нм.
Нм.
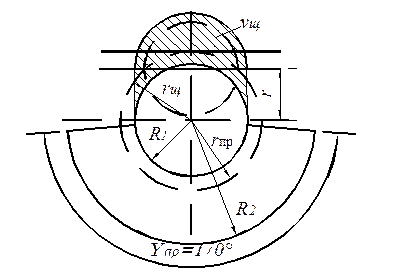
Рис. 3.15. Схема расчета противовеса
Приведенная масса противовеса, уравновешивающая момент сил инерции неуравновешенных вращающихся масс mII0 = mвра/b, откуда mII0 = = 7,58·0,139/0,275 = 3,83 кг.
Полная приведенная масса противовеса m0 = mI0 + mII0 = 0,44 + 3,83 = 4,27 кг.
Определяются основные размеры противовеса:
R1 = 0,0415 м;
R2 = 0,092 м;
θпр = 170°;
радиус инерции противовеса (рис. 3.15):
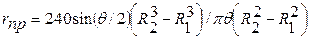 ;
;
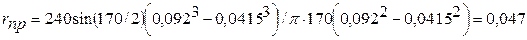 м.
м.
Масса противовеса находится по равенству mпр = m0r/rпр, откуда mпр = 4,27·0,038/0,047 = 3,45 кг.
Угол габарита противовеса:
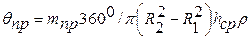 ,
,
где hср – средняя толщина противовеса.
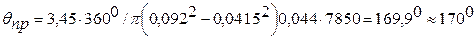 .
.
Угол, задаваемый первоначально, и угол, найденный из массы, противовеса совпадают, значит габариты противовеса были определены точно.
Расчет маховика
Планиметрированием находим площадки, образованные кривой суммарного противодействующего момента и прямой Мср и строим векторную диаграмму. Общая высота этой диаграммы определяет предельное изменение кинетической энергии маховика на протяжении одного оборота коленчатого вала. Определим требуемый момент инерции маховика [7, 8]:
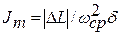 ,
,
где |ΔL| – максимальная избыточная работа, соответствующая наибольшей избыточной площадке на диаграмме противодействующего момента; δ – степень неравномерности движения, в случае привода от синхронного двигателя δ – 1/250.
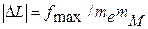 ,
,
где me = lx/2πr = 360/6,28٠0,038 = 1509 мм/Н – масштаб длин; mM = 1 мм/Н – масштаб моментов, тогда
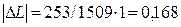 Нм;
Нм; 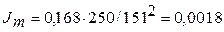 кгм2.
кгм2.
Как видно, требуемый момент инерции маховика мал. Его функции вполне может выполнять ротор электродвигателя. Потребность в установке дополнительного маховика отсутствует.
Дата добавления: 2021-06-28; просмотров: 478;











