Построение диаграмм суммарного противодействующего момента
Противодействующий момент, вызванный силами, действующими в ряду, в котором расположена i-я ступень, обозначим Мi. Он определяется по формуле
.
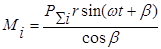Расчет моментов М1 и М2 представлен в виде таблицы 3.6. При построении суммарного противодействующего момента МΣ = М1 + М2 следует учесть смещение моментов, возникающих в каждом ряду от действия поршневых сил, на угол, соответствующий развалу цилиндров. Вращение коленчатого вала компрессора происходит против часовой стрелки, следовательно, поршень I ступени в своем движении отстает от поршня II ступени на угол ωt = 180º. Если за начало отсчета угла поворота кривошипа взять угол ωt = 0º, соответствующий положению поршня I ступени в ВМТ, то в этот момент поршень II ступени будет находиться в точке соответствующей ωt = 180º. Исходя из этого построение противодействующего момента М2 следует выполнять, начиная с точки, соответствующей ωt = 180º.
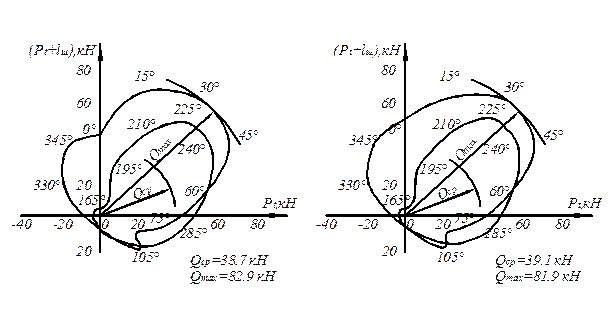а) б)
Рис. 3.6. Векторная диаграмма сил, действующих на шейку вала:
а) первой ступени; б) второй ступени
Дополнительно следует учесть момент сил трения вращательного движения:
.
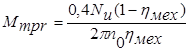Подставим значения в это выражение:
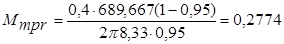кН.
Опустим ось абсцисс диаграммы на величину, соответствующую Мтрr. По диаграмме суммарного противодействующего момента определим значение среднего момента Мср и нанесем его на эту диаграмму. Эта величина пропорциональна потребляемой компрессором мощности: Nu = ωМср.
По диаграмме определяем Мср = 13,81 кН.
Получим Nu = 52,34·13,81 = 722,82 кВт.
Из термодинамического расчета Nu = 689,667 кВт. Погрешность укладывается в допустимые 5 %, следовательно, графические построения выполнены достаточно точно.
Таблица 3.6.
| ωt | М1 | М2 | МΣ |
| 0º | 0,000 | 0,000 | 0,000 |
| 15º | 4,089 | 1,114 | 10,407 |
| 30º | 8,410 | 3,725 | 24,271 |
| 45º | 10,544 | 7,113 | 35,313 |
| 60º | 8,394 | 8,944 | 34,676 |
| 75º | 5,314 | 9,160 | 28,949 |
| 90º | 2,930 | 8,190 | 22,240 |
| 105º | 3,288 | 6,790 | 20,156 |
| 120º | 0,774 | 4,308 | 10,164 |
| 135º | – 0,341 | – 0,533 | – 1,748 |
| 150º | – 0,554 | – 2,979 | – 7,067 |
| 165º | – 0,345 | – 2,484 | – 5,659 |
| 180º | 0,000 | 0,000 | 0,000 |
| 195º | 1,179 | 3,863 | 10,085 |
| 210º | 3,693 | 8,315 | 24,016 |
| 225º | 6,970 | 10,544 | 35,029 |
| 240º | 8,882 | 8,471 | 34,707 |
| 255º | 9,087 | 5,478 | 29,130 |
| 270º | 8,030 | 3,330 | 22,720 |
| 285º | 6,465 | 3,288 | 19,506 |
| 300º | 4,385 | 0,774 | 10,319 |
| 315º | – 0,468 | – 0,341 | – 1,618 |
| 330º | – 2,931 | 0,554 | – 4,754 |
| 345º | – 2,458 | – 0,345 | – 5,607 |
| 360º | 0,000 | 0,000 | 0,000 |
Планиметрированием найдем площадки, образованные кривой МΣ и прямой Мср и построим векторную диаграмму (рис. 3.7). Общая высота этой диаграммы определяет предельное изменение кинетической энергии маховика на протяжении одного оборота коленчатого вала.
Из диаграммы определили f = 8300 мм2.
Тогда требуемый момент инерции маховика:
,
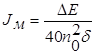где δ = 1/250 – степень неравномерности вращения.
,
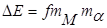где mα = 0,026 и mМ = 100 Нм/мм – масштабные коэффициенты на диаграмме.
Получим ΔЕ = 8300·100·0,026 = 21580 Нм.
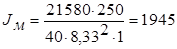Нм2.
Как видно, требуемый момент инерции маховика меньше момента инерции электродвигателя (см. разд. «подбор электродвигателя» в тепловом расчёте). Следовательно, нет необходимости в маховике, его функции вполне может выполнять ротор электродвигателя.
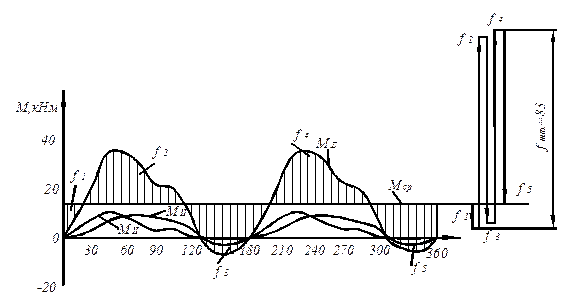
Рис. 3.7. Диаграмма суммарного противодействующего момента
Дата добавления: 2021-06-28; просмотров: 356;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
