Обратимые и необратимые процессы. Теорема Карно

Процесс называется обратимым, если он может быть проведен в обратном направлении через те же промежуточные состояния, что и прямой процесс, причем во всех остальных телах никаких изменений произойти не должно. Если же это сделать невозможно, то процесс называется необратимым.

Обратимые процессы являются идеализацией реальных процессов. Все реальные процессы в той или иной степени являются необратимыми. Степень необратимости определяется значительностью или незначительностью изменений, которые должны произойти в окружающих систему телах, чтобы провести обратный процесс. Процесс можно считать обратимым, если есть принципиальная возможность изменить его направление на обратное путем бесконечно малого изменения внешних условий, в которых находится система.

Обратимый процесс обязательно должен быть квазистатическим. Напомним, что квазистатический – это бесконечно медленный процесс, последовательность состояний, бесконечно мало отличающихся от равновесных.

Укажем некоторые признаки принципиально необратимых процессов.

Необратимы процессы, протекающие с конечными скоростями, т.к. если скорость процесса имеет определенное, отличное от нуля значение, она должна входить в число внутренних параметров системы. Тогда состояния системы в прямом и обратном процессах не могут быть тождественными – они всегда будут отличаться знаками скоростей. Это различие исчезнет только в пределе, когда процесс идет квазистатически – бесконечно медленно.

Процессы, в которых существенную роль играют силы трения, также необратимы из-за неизбежного при этом перехода механической энергии во внутреннюю. Обратный процесс запрещен постулатом Томсона.

Необратимость процесса теплообмена при конечной разности температур тоже обусловлена вторым началом термодинамики (формулировка Клаузиуса).

Рассмотренный в § 8 цикл Карно является обратимым циклом, т.к. он не включает в себя принципиально необратимых процессов. Обратимость этого цикла будет существенно использована в доказательстве первой теоремы Карно:

КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя Т₁ и холодильника Т₂, но не зависит от вида рабочего тела и конкретного устройства машины.

Для доказательства рассмотрим две машины Карно, имеющие общий нагреватель с температурой Т₁ и общий холодильник с температурой Т₂. Обозначим КПД одной машины (машины а) h_а, а второй (машины в) - h_в. Допустим, что h_а > h_в, и покажем, что это допущение приводит к противоречию со вторым началом термодинамики. Заставим машину а проходить цикл в прямом направлении. В процессе работы она забирает у нагревателя количество тепла Q_1а, передает холодильнику тепло Q_2а и совершает работу А_а = h_а×Q_1a =Q_1a – Q_2a, за счет которой можно поднять какой-либо груз на некоторую высоту. Остановим после этого машину а и используем потенциальную энергию поднятого груза, чтобы привести в действие машину в по обратному циклу (как холодильную машину). Проходя цикл Карно в обратном направлении, машина в будет забирать тепло у холодильника и отдавать тепло нагревателю. На рис. 10.1 схематически изображена работа машин а и в.

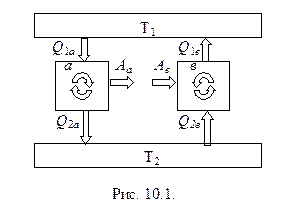Если для работы машины в по обратному циклу использовать всю энергию (А_а = А_в), накопленную в результате работы машины а, то количество тепла, переданное ею нагревателю Q_1в=А_в /h_в будет больше (из-за допущения, что h_а > h_в) количества тепла Q_1a = A_a /h_a, отобранного у нагревателя машиной а. В результате такой последовательной работы машин а и в, нагреватель получит положительное количество тепла Q = Q_1в – Q_1a. Такое же количество тепла Q = Q_2в – Q_2a, будет отобрано у холодильника. При этом никаких изменений в окружающих систему телах не произойдет. Таким образом, единственным результатом будет передача тепла от тела менее нагретого к телу более нагретому, что запрещено постулатом Клаузиуса. Поэтому предположение о том, что h_а > h_в неверно.

Точно так же неверно предположение h_в > h_а. Чтобы убедиться в этом, надо заставить машину в проходить цикл Карно в прямом направлении, а машину а - в обратном. При этом направления стрелок на рис. 10.1 изменятся на противоположные. Повторяя предыдущие рассуждения, вновь придем к противоречию. Следовательно, h_а = h_в, и теорема Карно доказана.

Следует отметить, что если только одна из машин, рассматриваемых при доказательстве теоремы, является обратимой, то доказательство проходит лишь «наполовину». Если обратимый цикл Карно реализуется машиной в, то можно доказать ложность предположения h_а > h_в. Поменять машины местами теперь нельзя. Только обратимая машина в обратном цикле делает все так же, как в прямом, но с противоположным знаком. В таком случае можно сформулировать следующее положение, называемое второй теоремой Карно:

КПД любой машины, совершающей цикл между двумя тепловыми резервуарами, не может превосходить КПД машины, работающей по циклу Карно с теми же температурами нагревателя и холодильника.

Таким образом, цикл Карно имеет максимально возможный КПД при заданных температурах нагревателя и холодильника.