Основные теоремы о сходящихся числовых рядах.

Числовые и функциональные ряды.

1. Основные понятия и определения.

Пусть 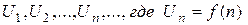- бесконечная числовая последовательность.

Выражение 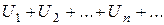называется бесконечным числовымрядом, а числа 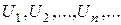- членами ряда; называется общим членом. Ряд часто записывают в виде .

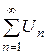Сумму первых и членов числового ряда обозначают через 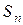и называют п-й частичной суммой ряда:

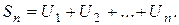
Ряд называется сходящимся, если его п-я частичная сумма 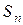при неограниченном возрастании и стремится к конечному пределу, т.е. если 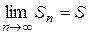. Число S называют суммой ряда. Если же п-я частичная сумма ряда при 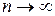не стремится к конечному пределу, то ряд называют расходящимся.

Ряд 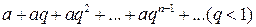, составленный из членов убывающей геометрической прогрессии, является сходящимся и имеет сумму .

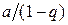Ряд 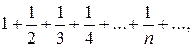называется гармоническим, расходится.

Основные теоремы о сходящихся числовых рядах.

Теорема.

Если сходится ряд

,

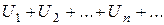то сходится и ряд

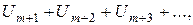
получаемый из данного ряда отбрасыванием первых 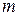членов (этот последний ряд называют 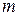- м остатком исходного ряда); наоборот, из сходимости 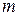- го остатка ряда вытекает сходимость данного ряда.

Теорем.

Если сходится ряд

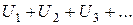
и суммой его является число S, то сходится и ряд

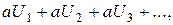
причем сумма последнего ряда равна аS.

Теорема.

Если сходится ряды

, ,

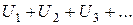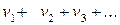имеющие соответственно суммы S и 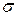, то сходится и ряд

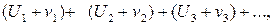
причем сумма последнего ряда равна S + .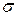

Теорема.

Если ряд

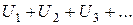
сходится, то 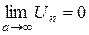, т.е. при 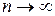придел общего члена сходящегося ряда равен нулю (необходимый признак сходимости ряда).

Таким образом, если 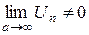, то ряд расходится.