Признаки сходимости рядов с положительными членами.
Первый признак сравнения. Пусть даны два ряда
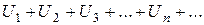 (1)
(1)
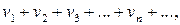 (2)
(2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. 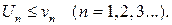 Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Тогда если сходится ряд (2), то сходится и ряд (1). Если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства 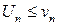 выполняются не при всех п, а лишь начиная с некоторого номера п = N.
выполняются не при всех п, а лишь начиная с некоторого номера п = N.
Второй признак сравнения. Если существует конечный и отличный от нуля предел 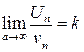 , то оба ряда
, то оба ряда 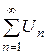 ,
, 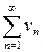 одновременно сходятся или одновременно расходятся.
одновременно сходятся или одновременно расходятся.
Радикальный признак Коши. Если для ряда
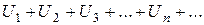
существует 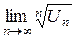 = q, то этот ряд сходится при q <1 и расходится при q >1.
= q, то этот ряд сходится при q <1 и расходится при q >1.
Признак Даламбера. Если для ряда
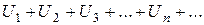
существует 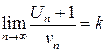 , то этот ряд сходится при k <1 и расходится при k >1.
, то этот ряд сходится при k <1 и расходится при k >1.
Интегральный признак Коши. Если f(x) при 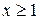 - непрерывная, положительная и монотонная убывающая функция, то ряд
- непрерывная, положительная и монотонная убывающая функция, то ряд 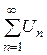 , где
, где 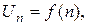 сходится или расходится в зависимости от того, сходится или расходится интеграл
сходится или расходится в зависимости от того, сходится или расходится интеграл
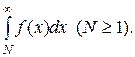
Пример. Исследовать сходимость ряда
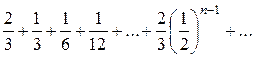
Решение: Данный ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем его сумму 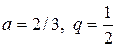 (знаменатель геометрической прогрессии). Следовательно
(знаменатель геометрической прогрессии). Следовательно
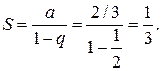
Пример. Исследовать сходимость ряда 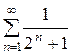 .
.
Решение: Член данного ряда меньше соответствующих членов ряда 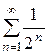 , т.е. ряда
, т.е. ряда 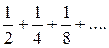
Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, сходится и данный ряд.
Пример . Исследовать сходимость ряда
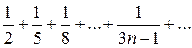
Решение: Сравним ряд с гармоническим рядом, у которого 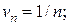
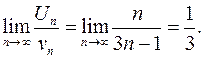
Следовательно, данный ряд расходится.
Пример. Исследовать сходимость ряда
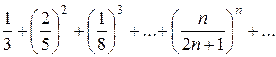
Решение: Здесь удобно применить признак Коши, поскольку 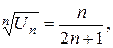 а предел
а предел
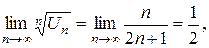
т.к. 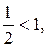 то ряд сходится.
то ряд сходится.
Пример.Исследовать сходимость ряда
 .
.
Решение: Применим признак Даламбера: имеем
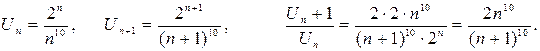
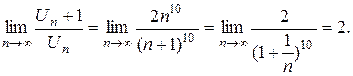
Дата добавления: 2017-03-12; просмотров: 3831;











