Применение степенных рядов.
Разложение в степенной ряд методом интегрирования.
Дифференцируя или интегрируя известные разложения функций в ряд Тейлора, можно получать разложения новых функций в степенные ряды. Так, например, интегрируя
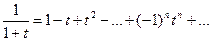 в пределах от 0 до x, |x|<1 (это законно, так как ряд равномерно сходится на отрезке с концами в точках 0 и x при |x|<1), получим формулу ln(1+x)=
в пределах от 0 до x, |x|<1 (это законно, так как ряд равномерно сходится на отрезке с концами в точках 0 и x при |x|<1), получим формулу ln(1+x)= 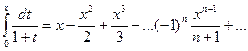
Ряд в правой части сходится при x=1 и, значит, сумма его непрерывна в этой точке.
Пример. Разложить по степеням x функцию arctg x.
Известно, что arctg x= 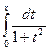 . Разложим подынтегральную функцию в степенной ряд:
. Разложим подынтегральную функцию в степенной ряд: 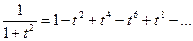 (из биномиального разложения, полагя t2=x).
(из биномиального разложения, полагя t2=x).
Этот ряд сходится для всех значений t, удовлетворяющих неравенствам –1<t<1.
Итак: arctg x =
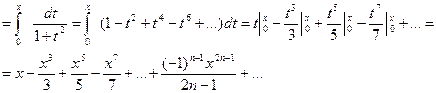
Вычисление значений функций с помощью рядов.
Пусть нужно вычислить значение функции f(x) при x=x0 с заданной точностью e.
Пусть f(x) разлагается в ряд: f(x)=a0+a1(x-a)+…+an(x-a)n+… в интервале (a-R, a+R) и точка x0 принадлежит интервалу.
Тогда, f(x0)=a0+a1(x0-a)+a2(x0-a)2+…
Взяв достаточное число первых членов, получим приближенное равенство, точность которого увеличивается с увеличением n. Абсолютная погрешность |f(x0)-Sn(x0)|=|Rn(x0)|, где Rn(x0)=an+1(x0-a)n+1+an+2(x0-a)n+2+…
Необходимо, чтобы |Rn(x0)|<e
Пример. Вычислить с точностью до 0,001 число e.
Решение. ex= 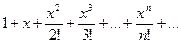
e1=1+1+ 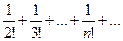
e»1+1+ 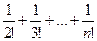
Rn(x)= 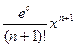 , где 0<c<x, при x=1
, где 0<c<x, при x=1
Rn(1)= 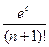 и так как eс<e1<3, получим Rn(1)<
и так как eс<e1<3, получим Rn(1)< 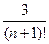 и подбором получим, что достаточно n=6 e»1+1+
и подбором получим, что достаточно n=6 e»1+1+ 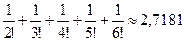 .
.
Приближенное вычисление интегралов.
Пример. 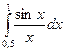 с точностью до 0,001.
с точностью до 0,001.
Так как sinx=x- 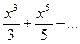 , то деля почленно на x, получим
, то деля почленно на x, получим 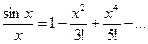
Интегрируя
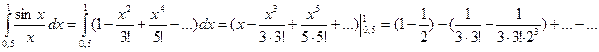
Ряд можно рассматривать как разность сходящихся знакопеременных рядов:
1- 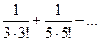
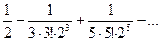
Погрешность не превосходит первого из отброшенных членов, и, подбором, видим, что достаточно трех скобок в разложении 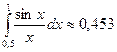
Пример. 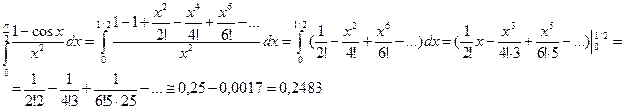
7.Тригонометрические ряды. Ряды Фурье
Тригонометрическим рядом называется ряд вида
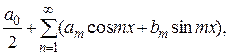 (6)
(6)
где 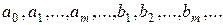 - действительные числа.
- действительные числа.
Рядом Фурье периодической функции 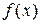 с периодом
с периодом 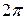 , определенной на интервале
, определенной на интервале 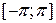 , называется ряд (6), коэффициенты которого определяются по формулам – Фурье:
, называется ряд (6), коэффициенты которого определяются по формулам – Фурье:
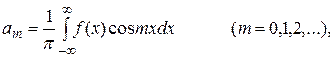
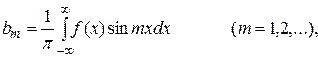
Если ряд (6) сходится, то его сумма S(x) есть периодическая функция с периодом 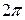 , т.е.
, т.е. 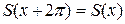 .
.
Теорема Дирихле. Пусть функция f(x) на интервале 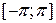 имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва I рода (т.е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке интервала
имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва I рода (т.е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке интервала 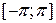 и сумма S(x) этого ряда:
и сумма S(x) этого ряда:
1) 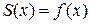 во всех точках непрерывности функции f(x), лежащих внутри интервала
во всех точках непрерывности функции f(x), лежащих внутри интервала 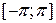 ;
;
2) 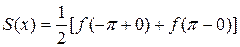 на концах интервала, т.е. при
на концах интервала, т.е. при 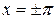 ;
;
3) 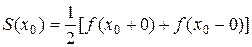 , где
, где 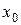 - точка разрыва I рода функции f(x).
- точка разрыва I рода функции f(x).
Если функция f(x) задана на интервале 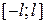 , где
, где 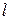 произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье
произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье
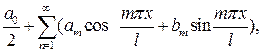
где
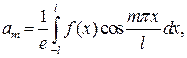

В случае, когда 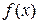 - четная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
- четная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
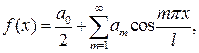
где 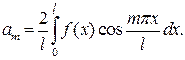
В случае, когда 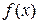 - нечетная функция, её ряд Фурье содержит только синусы, т.е.
- нечетная функция, её ряд Фурье содержит только синусы, т.е.
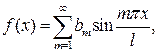
где 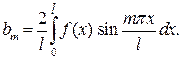
Если функция 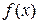 задана на интервале
задана на интервале 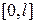 , то для разложения в ряд Фурье достаточно доопределить её на интервале
, то для разложения в ряд Фурье достаточно доопределить её на интервале 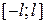 . Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках интервала
. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках интервала 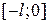 находились из условия
находились из условия 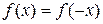 или
или 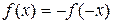 . В первом случае функция
. В первом случае функция 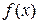 на интервале
на интервале 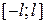 будет четной, а во втором – нечетной. При этом коэффициенте разложения такой функции (
будет четной, а во втором – нечетной. При этом коэффициенте разложения такой функции ( 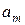 в первом случае и
в первом случае и 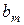 - во втором) можно определить по приведенным формулам для коэффициентов четных и нечетных функций.
- во втором) можно определить по приведенным формулам для коэффициентов четных и нечетных функций.
Пример. Разложить в ряд Фурье функцию с периодом 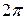 , определенную так
, определенную так
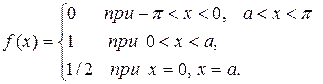
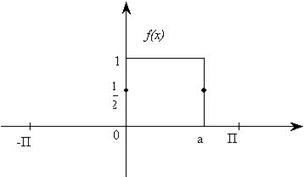
Решение: Из определения функции 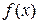 следует, что она удовлетворяет условиям Дирихле. Поэтому заданная функция разлагается в свой ряд Фурье.
следует, что она удовлетворяет условиям Дирихле. Поэтому заданная функция разлагается в свой ряд Фурье.
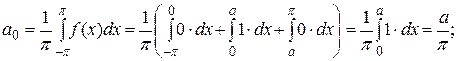
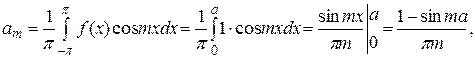
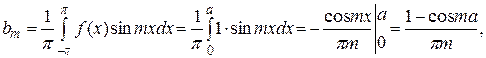
поэтому
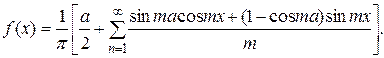
Пример. Разложить в ряд Фурье функцию с периодом 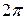 , определенную равенством.
, определенную равенством.
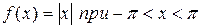
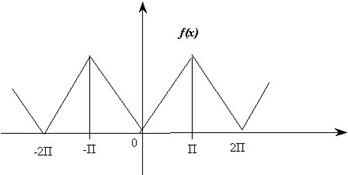
Решение: Эта непрерывная функция, очевидно, удовлетворяет условиям Дирихле и, следовательно, разлагается в свой ряд Фурье, она четная, поэтому
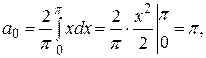
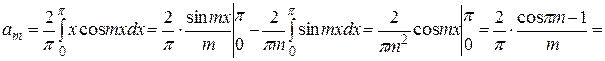
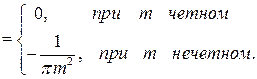
Следовательно,
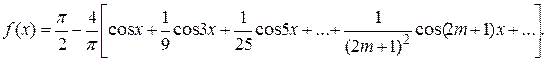
Пример. Разложить в ряд Фурье функцию определенную равенством
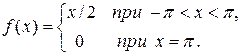
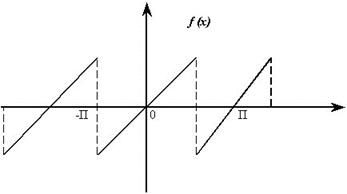
Решение: Эта функция разрывная, удовлетворяет условиям Дирихле, и, следовательно, разлагается в свой ряд Фурье. Функция нечетная, поэтому
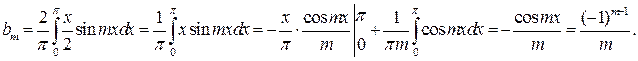
Следовательно
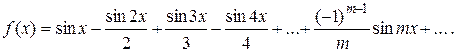
Пример. Функцию 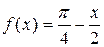 разложить в ряд косинусов на интервале
разложить в ряд косинусов на интервале 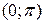 .
.
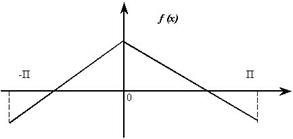
Решение: Продолжая заданную функцию четным образом, как показано на рис. 17 пунктиром, будем иметь
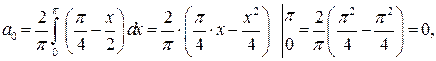
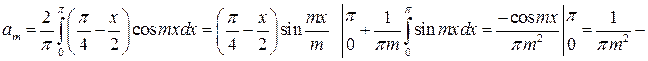
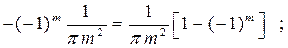
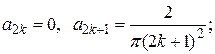
поэтому 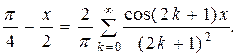
Пример. Разложить в ряд Фурье функцию 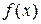 с периодом 4, график функции на интервале – периоде (-2,2) изображен на рис.
с периодом 4, график функции на интервале – периоде (-2,2) изображен на рис.
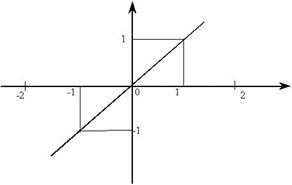
Решение. Заданная функция нечетная с периодом 2 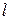 =4, поэтому
=4, поэтому
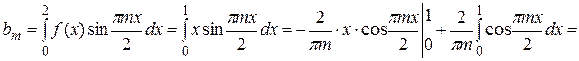
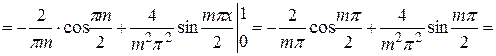
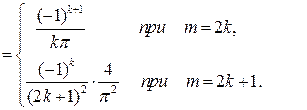
В результате получим
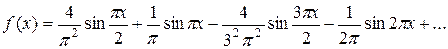
Дата добавления: 2017-03-12; просмотров: 1661;











