Полный дифференциал. Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Основные понятия и определения.
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
z = f(x, y)
Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Окрестностью точкиМ0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию 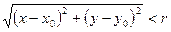 .
.
Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие
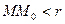
также верно и условие 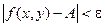 .
.
Записывают: 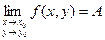
Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М0(х0, у0), если
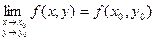 (1)
(1)
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрывафункции f(x, y). Это может быть в следующих случаях:
1) Функция z = f(x, y) не определена в точке М0(х0, у0).
2) Не существует предел 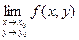 .
.
3) Этот предел существует, но он не равен f( x0, y0).
Свойства функций нескольких переменных, связанные с их непрерывностью.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка
N(x0, y0, …), такая, что для остальных точек верно неравенство
f(x0, y0, …) ³ f(x, y, …)
а также точка N1(x01, y01, …), такая, что для всех остальных точек верно неравенство
f(x01, y01, …) £ f(x, y, …)
тогда f(x0, y0, …) = M – наибольшее значение функции, а f(x01, y01, …) = m – наименьшее значениефункции f(x, y, …) в области D.
Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка
N0(x0, y0, …) такая, что f(x0, y0, …) = m.
Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.
Свойство. Функция f(x, y, …), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство 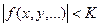 .
.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х1, y1) и (х2, у2) области, находящихся на расстоянии, меньшем D, выполнено неравенство
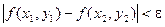
2. Частные производные. Частные производные высших порядков.
Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.
Можно записать
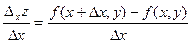 .
.
Тогда 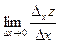 называется частной производнойфункции z = f(x, y) по х.
называется частной производнойфункции z = f(x, y) по х.
Обозначение: 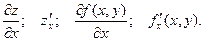
Аналогично определяется частная производная функции по у.
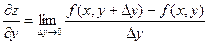
Геометрическим смысломчастной производной (допустим 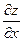 ) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
Если функция f(x, y) определена в некоторой области D, то ее частные производные 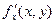 и
и 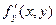 тоже будут определены в той же области или ее части.
тоже будут определены в той же области или ее части.
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второго порядка.
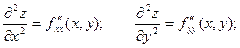
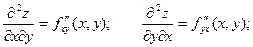
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Частные производные вида 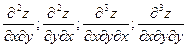
 и т.д. называются смешанными производными.
и т.д. называются смешанными производными.
Теорема. Если функция f(x, y) и ее частные производные 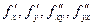 определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:
определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:
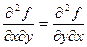 .
.
Т.е. частные производные высших порядков не зависят от порядка дифференцирования.
Аналогично определяются дифференциалы высших порядков.
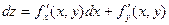
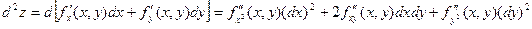
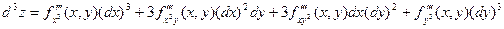
…………………
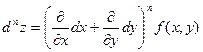
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего с скобках выражения.
Полный дифференциал. Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
Выражение 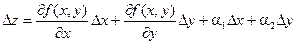 называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
Полным дифференциаломфункции z = f(x, y) называется главная линейная часть относительно Dх и Dу приращения функции Dz в точке (х, у).
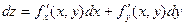
Для функции произвольного числа переменных:
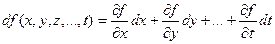
Пример 3.1. Найти полный дифференциал функции 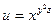 .
.
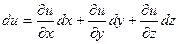
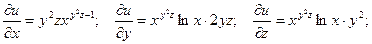
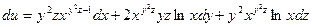
Пример 3.2. Найти полный дифференциал функции 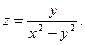
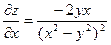
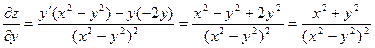
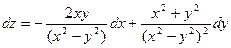
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Нормальюк поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
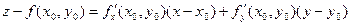 .
.
Уравнение нормали к поверхности в этой точке:
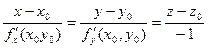
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример 3.3. Найти уравнения касательной плоскости и нормали к поверхности
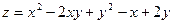
в точке М(1, 1, 1).
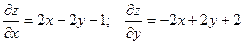
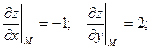
Уравнение касательной плоскости:
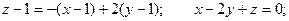
Уравнение нормали:
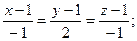
Дата добавления: 2017-03-12; просмотров: 3912;











