Наибольшее и наименьшее значения функции в области.
Дифференцируемая в ограниченной замкнутой области 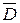 функция
функция 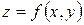 достигает своих наибольшего и наименьшего значений, либо в стационарной точке, лежащей внутри области
достигает своих наибольшего и наименьшего значений, либо в стационарной точке, лежащей внутри области 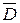 , либо на границе этой области.
, либо на границе этой области.
Алгоритм поиска наибольшего и наименьшего значений:
Найти все критические точки функции 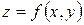 , лежащие внутри области
, лежащие внутри области 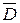 .
.
Исследовать поведение функции 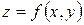 на границе области
на границе области 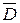 .
.
Вычислить значения функции во всех найденных точках и выбрать из них наибольшее и наименьшее.
Пример 7.1. Найти наибольшее и наименьшее значения функции 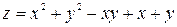 в области, ограниченной линиями:
в области, ограниченной линиями:
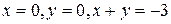 .
.
1) находим стационарную точку, лежащую в области:
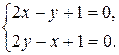 →
→ 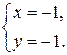 →
→ 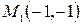 .
.
2) исследуем данную функцию на границе области.
a) При 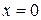 функция z имеет выражение:
функция z имеет выражение:
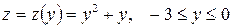 .
.
Критические точки на границе 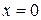 находим из уравнения:
находим из уравнения:
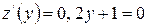 . Отсюда
. Отсюда 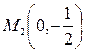 .
.
b) При 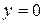 для функции z имеем выражение:
для функции z имеем выражение:
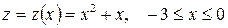 .
.
Критические точки на границе 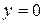 находим из уравнения:
находим из уравнения: 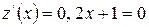 . Отсюда
. Отсюда 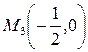 .
.
c) При 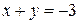 для функции z имеем выражение:
для функции z имеем выражение:
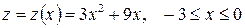 .
.
Критические точки на границе 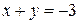 находим из уравнения:
находим из уравнения: 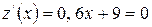 . Отсюда
. Отсюда 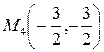 .
.
вычисляем значения в критических точках 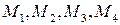 , а также в точках
, а также в точках 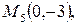
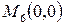 ,
, 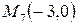 :
:
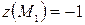 ,
, 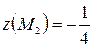 ,
, 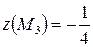 ,
, 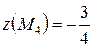 ,
, 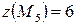 ,
, 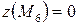 ,
, 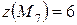 .
.
Итак, наибольшее значение: 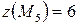 ,
, 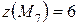 ; наименьшее значение:
; наименьшее значение: 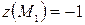 .
.
Дата добавления: 2017-03-12; просмотров: 2185;











