Пример расчета коэффициента корреляции Спирмэна.

<19 20 212223 24 25 >

Необходимо определить по Таблице 2, существует ли связь между количеством часов, посвященных студентом подготовке к тестовому экзамену по статистике, и итоговым количеством правильных ответов (и, соответственно, итоговой оценкой). Тестирование включает в себя 100 вопросов из банка тестовых заданий.

Решение:

Составляем вариационный ряд x и ранжируем:

x
R_x		2.5	2.5	4.5	4.5

Составляем вариационный ряд y и ранжируем:

y
R_y

Для удобства расчета заполняем следующую таблицу:

x
y
R_x	2.5	4.5	4.5	2.5
R_y
R_y- R_x	1.5	0.5	-1.5	-0.5
(R_y- R_x)²	2.25	0.25	2.25	0.25

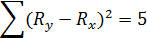
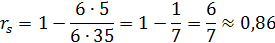
Таким образом, получено, что исследуемая корреляционная связь является прямой и сильной.

В ходе корреляционного анализа или анализа корреляционной связи решается целая группа взаимосвязанных задач:

1) Установление направления (прямая или обратная) и формы (линейная или нелинейная) корреляционной связи.

2) Оценка тесноты (силы, плотности) корреляционной связи.

3) Оценка репрезентативности статистических оценок взаимосвязей, полученных по выборочным данным (величина ошибки, доверительный интервал, уровень значимости).

4) Установление величины детерминации (доли взаимовлияния) коррелируемых факторов.

Таким образом, статистические методы изучения связи между переменными зависят от:

· характера переменных (качественные, количественные)

· характера распределения количественных переменных (нормальное, ненормальное, неизвестное)

· числа наблюдений (большое, малое)

· взаимоотношения между наблюдениями (зависимые, независимые).

Статистические методы изучения связи между переменными могут быть:

· однофакторными, т.е. принимающими во внимание только взаимоотношения между двумя анализируемыми переменными

· многофакторными, т.е. учитывающими влияние на изучаемую связь между двумя переменными со стороны некоторых других переменных.

<19 20 212223 24 25 >

Дата добавления: 2016-06-05; просмотров: 1632;

Поиск по сайту

Узнать еще