Критерий Манна-Уитни – ранговый критерий для сравнения независимых выборок.
Рассмотрим этот критерий на примере. Допустим, получены следующие данные о величине ЧСС в двух группах детей 2-3 и 4-5 лет:
x(2-3 года): 102, 87, 105, 110, 99, 90 (nx=6)
y(4-5 лет): 98, 100, 88, 92, 83, 95, 100, 92, 85, 94 (ny=10)
Сначала выборки смешивают и ранжируют как одну совокупность:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| x | 83 | 85 | 87 | 88 | 90 | 92 | 92 | 94 | 95 | 98 | 99 | 100 | 100 | 102 | 105 | 110 |
| R | 1 | 2 | 3 | 4 | 5 | 6.5 | 6.5 | 8 | 9 | 10 | 11 | 12.5 | 12.5 | 14 | 15 | 16 |
Полученные ранги приписывают числам исходных рядов и подсчитывают их суммы:
| x(2-3 года) | 102 | 87 | 105 | 110 | 99 | 90 | |||||
| Rx | 14 | 3 | 15 | 16 | 11 | 5 | 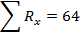
| ||||
| y(4-5 лет) | 98 | 100 | 88 | 92 | 83 | 95 | 100 | 92 | 85 | 94 | |
| Ry | 10 | 12.5 | 4 | 6.5 | 1 | 9 | 12.5 | 6.5 | 2 | 8 | 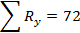
|
Далее полученные суммы включают в специальную формулу для подсчета критерия U:
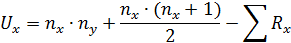
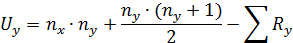
В нашем примере получаем 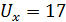 ,
, 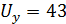 .
.
В качестве 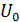 берут меньшее из полученных значений (т.е. 17) и сравнивают его с критическими значениями, взятыми из специальной таблицы:
берут меньшее из полученных значений (т.е. 17) и сравнивают его с критическими значениями, взятыми из специальной таблицы: 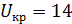 для
для 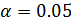 и
и 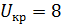 для
для 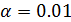 . Поскольку
. Поскольку 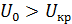 , нулевую гипотезу отвергнуть нельзя даже для
, нулевую гипотезу отвергнуть нельзя даже для 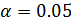 и различие уровней ЧСС следует признать статистически незначимым.
и различие уровней ЧСС следует признать статистически незначимым.
Чтобы говорить о статистически значимых различиях, должно выполняться условие 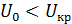 .
.
Критерий парных сравнений Вилкоксона– ранговый критерий для сравнения зависимых выборок.
Рассмотрим его на примере. У 10 здоровых взрослых людей измеряли кровяное давление после введения кофеина и плацебо. Получены следующие данные для «верхнего», систолического давления СД:
| x(кофеин) | ||||||||||
| y(плацебо) |
Возникает вопрос, можно ли на основании этих данных полагать, что кофеин оказывает физиологическое действие.
Вначале значения одного ряда строго попарно вычитают из значений другого с учетом знака разницы d. Вычтем нижний ряд из верхнего:
| x(кофеин) | ||||||||||
| y(плацебо) | ||||||||||
| d | -4 | -10 |
Далее разницы ранжируют по известным правилам, но при этом не учитывают знак разницы (т.е. ранжируют по модулю). Нулевую пару отбрасывают.
| d | -4 | -10 | |||||||
| R | 1.5 | 1.5 | 7.5 | 7.5 |
Отдельно суммируют ранги для положительных и отрицательных разниц. В нашем случае получаем: 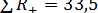 ,
, 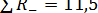 . В качестве значения критерия Tz берут меньшую сумму независимо от знака, т.е. Tz =11,5. Сравниваем это значение с «критическим» из специальной таблицы, входом в которую является число сравниваемых пар, но лишь тех, которые не дают нулевые разницы. В нашем случае таковых 9. Тогда Tкр = 6 для
. В качестве значения критерия Tz берут меньшую сумму независимо от знака, т.е. Tz =11,5. Сравниваем это значение с «критическим» из специальной таблицы, входом в которую является число сравниваемых пар, но лишь тех, которые не дают нулевые разницы. В нашем случае таковых 9. Тогда Tкр = 6 для 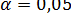 и Tкр =2 для
и Tкр =2 для 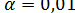 . Поскольку
. Поскольку 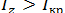 даже для первого уровня значимости, различий уровней СД нулевую гипотезу отвергнуть нельзя и различия не являются статистически значимыми (р<0,05). Иными словами, у нас нет пока оснований утверждать, что действие кофеина носит исключительно физиологический характер.
даже для первого уровня значимости, различий уровней СД нулевую гипотезу отвергнуть нельзя и различия не являются статистически значимыми (р<0,05). Иными словами, у нас нет пока оснований утверждать, что действие кофеина носит исключительно физиологический характер.
Смысл теста состоит в следующем. Если бы мы имели бесконечно большой ряд случайных разниц, то число и величина положительных разниц равнялись бы числу отрицательных и, соответственно, суммы их рангов были бы равны. На конечном и ограниченном числовом массиве опять же чисто случайно может иметь место «перекос» в сторону преимущественно положительных или отрицательных разниц. Это обстоятельство и учитывается в критических значениях критерия.
Tкр – это граница между практически возможными и практически невозможными значениями критерия. Соответственно, если 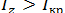 , то полученная нами сумма рангов с достаточно высокой вероятностью могла возникнуть чисто случайно и о сдвиге одного числового ряда относительно другого ничего определенного сказать нельзя. Это недостоверное различие. Если же
, то полученная нами сумма рангов с достаточно высокой вероятностью могла возникнуть чисто случайно и о сдвиге одного числового ряда относительно другого ничего определенного сказать нельзя. Это недостоверное различие. Если же 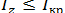 , то наблюдаемое различие положительных и отрицательных разниц не могло быть получено случайным образом. Это означает, что смещение значений в сопоставляемых числовых рядах объясняется действием какой-то систематически действующей, неслучайной причины, т.е. носит статистически достоверный (устойчивый и прогнозируемый) характер.
, то наблюдаемое различие положительных и отрицательных разниц не могло быть получено случайным образом. Это означает, что смещение значений в сопоставляемых числовых рядах объясняется действием какой-то систематически действующей, неслучайной причины, т.е. носит статистически достоверный (устойчивый и прогнозируемый) характер.
Как было показано выше, пары, имеющие одинаковые числовые значения и, соответственно, дающие нулевые разницы, исключаются из рассмотрения. И если таких случаев много, то «жесткость» критерия нарастает, поскольку Tкр тем меньше, чем меньше сравниваемых пар. Соответственно, увеличивается число ситуаций, когда нулевую гипотезу отвергнуть невозможно, и различие будет считаться незначимым. Более того, если число пар окажется меньше 6, то критерий Вилкоксона вообще перестанет «работать»: 6 - минимальное число пар, для которого еще существует Tкр. Для меньшего числа его просто невозможно рассчитать. А подобные ситуации в медико-биологической практике возникают довольно часто, поскольку многие измерения неизбежно приходится выполнять с достаточно высокой степенью грубости, и вероятность появления совпадающих значений здесь все еще весьма высока.
Критерий согласия Пирсона (критерий 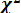 )
)
Критерии согласия позволяют определить степень соответствия эмпирических и теоретических распределений вероятностей, а также двух эмпирических распределений, полученных, например, в «контроле» и «опыте» или в различных вариантах «опыта» или «наблюдения». Этот критерий позволяет проверить гипотезу о схожести фактического, полученного на практике, распределения вероятностей случайной величины и теоретического.
Данный критерий может использоваться, например, для сравнения частот встречаемости качественных или порядковых признаков в выборочных совокупностях.
Критерий Пирсона записывается следующим образом:

где k – число классов ряда распределения, 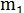 – фактические (наблюдаемые) частоты встречаемости случайной величины в каждом i-ом классе (в виде целых чисел),
– фактические (наблюдаемые) частоты встречаемости случайной величины в каждом i-ом классе (в виде целых чисел), 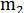 – теоретически ожидаемые (вычисленные) частоты для данного класса,
– теоретически ожидаемые (вычисленные) частоты для данного класса, 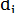 – разница между ними.
– разница между ними.
Таким образом, 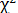 представляет собой вовсе не квадрат какого-то числа, а суммупо всем классам распределения данной случайной величины (от 1-го до k-го) величины квадратов разницы фактических и теоретических частот в каждом классе, отнесенных к теоретическим частотам для этих же классов.
представляет собой вовсе не квадрат какого-то числа, а суммупо всем классам распределения данной случайной величины (от 1-го до k-го) величины квадратов разницы фактических и теоретических частот в каждом классе, отнесенных к теоретическим частотам для этих же классов.
Допустим, что по каждому классу распределения 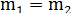 , т.е. фактические (наблюдаемые) и ожидаемые (вычисленные) частоты идеально совпадают. Тогда
, т.е. фактические (наблюдаемые) и ожидаемые (вычисленные) частоты идеально совпадают. Тогда 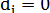 и, соответственно,
и, соответственно, 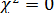 . Понятно, что такого рода ситуация может иметь место только в том случае, когда форма эмпирического распределения абсолютно идентична форме теоретической модели, рассчитанной по эмпирическим данным.
. Понятно, что такого рода ситуация может иметь место только в том случае, когда форма эмпирического распределения абсолютно идентична форме теоретической модели, рассчитанной по эмпирическим данным.
Допустим теперь, что 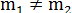 хотя бы для одного из сравниваемых классов эмпирического и теоретического распределений, то есть для какого-то одного из них
хотя бы для одного из сравниваемых классов эмпирического и теоретического распределений, то есть для какого-то одного из них 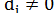 . Поскольку мы имеем дело с «суммой квадратов», то
. Поскольку мы имеем дело с «суммой квадратов», то 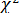 автоматически станет больше нуля. Чем больше будет таких различий для разных классов и чем значительнее будут сами различия, тем больше будет «набегать» сумма квадратов. Следовательно, при различии наблюдаемых и ожидаемых частот сравниваемых распределений
автоматически станет больше нуля. Чем больше будет таких различий для разных классов и чем значительнее будут сами различия, тем больше будет «набегать» сумма квадратов. Следовательно, при различии наблюдаемых и ожидаемых частот сравниваемых распределений 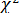 может принимать любые положительные значения, вплоть до бесконечности. Нетрудно представить, что чем менее схожей будет форма сравниваемых распределений, тем большие числовые значения будет принимать
может принимать любые положительные значения, вплоть до бесконечности. Нетрудно представить, что чем менее схожей будет форма сравниваемых распределений, тем большие числовые значения будет принимать 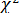 и, само собой, наоборот. Иными словами,
и, само собой, наоборот. Иными словами, 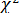 является мерой сходства/различия формы сравниваемых распределений вероятностей.
является мерой сходства/различия формы сравниваемых распределений вероятностей.
Технология использования критерия «Хи-квадрат» чрезвычайно проста. По приведенной выше формуле подсчитывается «экспериментальное» значение «Хи-квадрат» 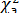 , которое сравнивают с табличным или «критическим» значением
, которое сравнивают с табличным или «критическим» значением 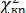 , взятым сообразно наличному числу степеней свободы). Далее, как всегда, проверяется выполнение двух неравенств:
, взятым сообразно наличному числу степеней свободы). Далее, как всегда, проверяется выполнение двух неравенств:
- если 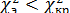 , то разница наблюдаемых (фактических) и ожидаемых (теоретических) частот сравниваемых распределений незначительна и не выходит за рамки ее собственных случайных колебаний, не превышает критического порога «возможного». Это не позволяет отвергнуть «нулевую гипотезу», согласно которой имеющие место различия частот носят случайный характер;
, то разница наблюдаемых (фактических) и ожидаемых (теоретических) частот сравниваемых распределений незначительна и не выходит за рамки ее собственных случайных колебаний, не превышает критического порога «возможного». Это не позволяет отвергнуть «нулевую гипотезу», согласно которой имеющие место различия частот носят случайный характер;
- если 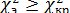 , то разница наблюдаемых (фактических) и ожидаемых (теоретических) частот сравниваемых распределений столь велика, что выходит за рамки ее собственных случайных колебаний. Самопроизвольное появление такого значения «Хи-квадрат» относится к разряду невозможных событий. Следовательно, различие форм эмпирического и теоретического распределений обусловлено действием некого систематически действующего фактора, и эмпирическое распределение на принятом уровне значимости не может рассматриваться в качестве случайной модификации теоретической модели.
, то разница наблюдаемых (фактических) и ожидаемых (теоретических) частот сравниваемых распределений столь велика, что выходит за рамки ее собственных случайных колебаний. Самопроизвольное появление такого значения «Хи-квадрат» относится к разряду невозможных событий. Следовательно, различие форм эмпирического и теоретического распределений обусловлено действием некого систематически действующего фактора, и эмпирическое распределение на принятом уровне значимости не может рассматриваться в качестве случайной модификации теоретической модели.
Однако, при использовании критерия Пирсона существуют следующие ограничения:
· во-первых, объем выборочной совокупности должен быть не менее 50;
· во-вторых, допускается сравнение только абсолютных, а не относительных частот, т.е. количества значений случайной величины, попадающей в каждый класс распределения «в штуках»
· в-третьих, если в теоретическом (вычисленном) распределении встречается класс, в котором число значений менее пяти, то его еще до начала вычисления критерия объединяют с соседним, складывая их частоты. При этом такое же сокращение числа классов, независимо от фактического количества частот в них, производят и в эмпирическом распределении.
Отметим, что в современных программных пакетах математико-статистической обработки данных SPSS и Statistica все операции, необходимые для расчета статистических критериев автоматизированы. Главной задачей пользователя является правильный выбор статистического критерия в каждом конкретном случае. Программа выдает полный отчет о результатах расчетов с указанием уровня значимости нулевой гипотезы. Подробное использование этих статистических программ изложено в электронных и печатных руководствах пользователя.
Дата добавления: 2016-06-05; просмотров: 2699;











