Тяговые свойства асинхронного ТД.
В асинхронном ТД используется взаимодействие вращающегося магнитного поля статора с током, наведенным этим полем в роторе. Вращающий момент асинхронного ТД описывается следующей формулой:
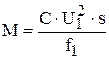 ,
,
где С – постоянная, зависящая от параметров двигателя;
U1 – питающее напряжение;
s – скольжение ротора;
f1 – частота питающего напряжения.
| Сравниваемый параметр | Коллекторные | Бесколлекторные | ||||
| Постоянного тока | Пульсирующего тока | Однофазного тока | Трехфазного тока | |||
| Пониженной частоты | Нормальной частоты | Асинхронные | Синхронные | |||
| Предельная мощность, кВт | ||||||
| Напряжение, В | ||||||
| КПД, % | 90…93 | 89…90 | 86…88 | 93…94 | ||
| Удельная масса, кг/кВт | 6,8…7,5 | 4,5…5,5 | 3,9 | 8,7 | 1,6…3,0 | 3,7…4,0 |
| Относительная стоимость | 1,4 | 1,0 | 1,1 | 1,6 | 0,5 | 0,75 |
| Регулируемые величины | Uд, Iв | Uд, Iв | Uд, Iв | Uд | Uд, fд, f2 | Uд, fд, Iв |
Для питания АТД на ЭПС постоянного тока необходимо иметь автономный инвертор напряжения или тока. На ЭПС переменного тока кроме автономного инвертора необходим выпрямитель. И выпрямитель и инвертор могут быть объединены в одном полупроводниковом устройстве – преобразователе числа фаз (ПЧФ). На современном этапе развития силовой полупроводниковой техники выгоднее на ЭПС постоянного тока дополнительно иметь входной импульсный преобразователь для регулирования величины напряжения, подводимого к ТД.
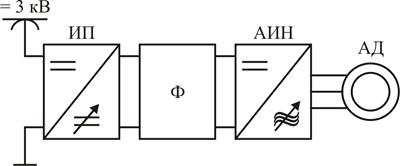
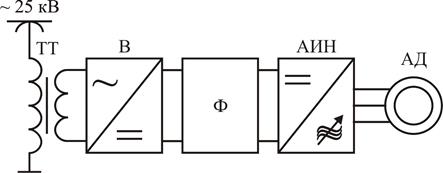
Т.к. нагрузка ТД в эксплуатации может изменяться в широких пределах, то имея сложную многофункциональную систему управления важно и должно соблюдать условия, при которых ТД работает в наиболее экономичном режиме:
DРmin = (DРм + DРс + DР2) = const.
В первом приближении считают, что механические DРм и магнитные DРс потери в двигателе не зависят от нагрузки, т.е. от тока ротора. Потери в роторе
DР2 = М × (w1 – wвр),
где w1 – угловая частота вращения магнитного поля статора;
wвр – угловая частота вращения ротора.
Рассмотрим, при каком условии потери минимальны. Так как мы условились, что потери механические и магнитные не зависят от нагрузки, то условие минимума потерь сводится к минимуму потерь в роторе:
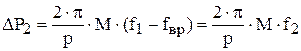 ,
,
где fвр – частота вращения ротора;
f2 – частота тока ротора.
Следовательно, условие
DРmin = const
преобразуется в условие
f2 min = (f1 – fвр)min = const.
Для выявления способов реализации этого условия рассмотрим два режима работы двигателя. Допустим, что в первом режиме статор питается напряжением U1 с частотой f1, а в другом – соответственно U1' и f1'. Скольжение ротора в этих режимах равно:
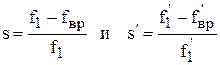 .
.
Вращающий момент в этих режимах будет соответственно равен:
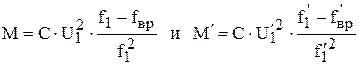 .
.
Найдем соотношение моментов в этих режимах при условии
f1 – fвр = f1' – fвр' = const:
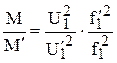 .
.
Отсюда
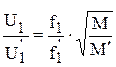 .
.
Этот закон оптимального частотного управления асинхронным двигателем был сформулирован М.П.Костенко в 1925 г. Из этого выражения следует, что оптимальный режим работы асинхронного двигателя определяется соотношением трех его параметров – напряжения и частоты питающего напряжения, а так же вращающего момента. Изменяя соотношение этих составляющих таким образом, чтобы соблюдалось условие минимума потерь т.е. условие работы с максимальным КПД и cosj. При больших нагрузках следует учитывать падение напряжения в обмотке ротора и для получения наилучших показателей вносить коррективы в закон регулирования. С этой целью на электровозах применяется система автоматического регулирования режимов работы ТД.
Поскольку для электрической тяги удобнее иметь выражение закона регулирования не от частоты питающего напряжения и момента, а от скорости и силы тяги, то выражение закона Костенко преобразуется следующим образом:
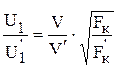 .
.
Выражение получено с допущением, что на рабочей части характеристики скорость движения пропорциональна частоте питающего напряжения без учета скольжения:
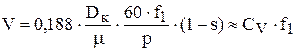 ,
,
а сила тяги, как известно, пропорциональна вращающему моменту без всяких допущений:
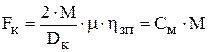 .
.
 Для ЭПС наиболее характерен следующий закон регулирования: до скорости выхода на номинальную характеристику поддерживается постоянство силы тяги, а затем – постоянство мощности.
Для ЭПС наиболее характерен следующий закон регулирования: до скорости выхода на номинальную характеристику поддерживается постоянство силы тяги, а затем – постоянство мощности.
Постоянство силы тяги означает постоянство вращающего момента. Вращающий момент определяется взаимодействием магнитного потока статора и тока ротора, приведенного к обмотке статора (I2'). Следовательно, постоянство вращающего момента равносильно I2' = const. Ток статора можно представить как сумму векторов тока холостого хода и тока ротора, приведенного к обмотке статора:
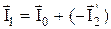 .
.
Следовательно, постоянство тока ротора равносильно постоянству тока статора и закон регулирования при постоянстве силы тяги будет выглядеть следующим образом:
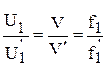 .
.
Т.е. для поддержания постоянной силы тяги необходимо с ростом скорости повышать напряжение питания, пропорционально скорости или частоте.
После выхода на номинальную характеристику целесообразно поддерживать постоянной мощность двигателя. Поскольку
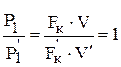 ,
,
то
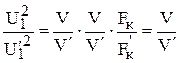 .
.
Следовательно
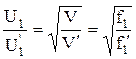 .
.
Иными словами, для поддержания постоянства мощности необходимо с ростом скорости изменять питающее напряжение пропорционально корню квадратному из его частоты. Рост питающего напряжения требует более мощной изоляции обмотки статора, и, следовательно, приведет к увеличению габаритных размеров ТЭД.
В случае реализации закона постоянства питающего напряжения мощность и ток статора будет изменяться обратно пропорционально скорости движения, а сила тяги – обратно пропорционально квадрату скорости:
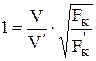 ; Þ
; Þ 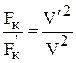 .
.
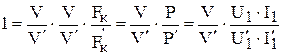 ; Þ
; Þ 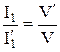 .
.
Так как в этом случае сила тяги падает слишком интенсивно, рационально реализовать гибридный закон регулирования: при достижении максимальной мощности напряжение питания еще не достигает своего максимального значения. Реализуется режим постоянства мощности. При достижения напряжением питания максимума – режим постоянства питающего напряжения.
Логично предположить, что система автоматического управления способна реализовать алгоритм поддержания постоянной скорости движения. Как следует из формулы, постоянство скорости соответствует постоянству частоты питающего напряжения. В этом случае
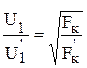 ,
,
т.е. при постоянной скорости движения необходимо изменять питающее напряжение пропорционально корню квадратному из силы тяги.
 Таким образом, одним из достоинств асинхронного ТД является возможность с помощью системы управления реализовывать различную жесткость характеристик: при постоянстве частоты реализуется жесткая характеристика (хороша при необходимости использовать максимальную силу по условиям сцепления), при постоянстве напряжения – мягкую.
Таким образом, одним из достоинств асинхронного ТД является возможность с помощью системы управления реализовывать различную жесткость характеристик: при постоянстве частоты реализуется жесткая характеристика (хороша при необходимости использовать максимальную силу по условиям сцепления), при постоянстве напряжения – мягкую.
Максимальную частоту питающего напряжения выбирают исходя из максимальной скорости движения ЭПС и параметров ТД и тяговой передачи:
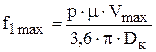 .
.
Минимальную частоту выбирают из условия трогания с места при условии, что ТД реализует силу тяги, превышающую номинальную на 30…50% при минимальном токе статора.
Дата добавления: 2017-03-12; просмотров: 2251;











