Аналитический расчет нагревания ТД.
Современные ТД представляют собой очень сложные конструкции, состоящие из большого числа частей сложной геометрической формы. Все эти части изготовлены из различных материалов, имеют разную массу, разные условия теплопередачи. В различных частях ТД выделяется неодинаковое количество тепла. Вследствие сложности тепловых процессов в ТД точный аналитический расчет его нагревания крайне затруднителен. Поэтому для моделирования нагревания ТД прибегают к упрощениям. Наиболее распространенный способ, дающий удовлетворительные результаты, основан на представлении ТД однородным твердым телом.
Нагревание любой обмотки ТД определяется, в основном, электрическими потерями в ней I2×r и магнитными потерями в прилегающих к обмотке стальных частях DРс. Потери в стали определяют по опытным кривым, снятым на стенде. С достаточной точностью потери энергии на нагрев обмотки можно описать следующим уравнением:
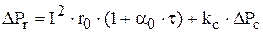 .
.
Здесь r0 – сопротивление обмотки при температуре окружающего воздуха;
a0 – температурный коэффициент;
t – текущий перегрев обмотки (превышение температуры обмотки над температурой окружающей среды);
kс – опытный поправочный коэффициент потерь в стали.
Рассмотрим процесс нагревания обмотки ТД, приняв ее за однородное твердое тело с приведенными тепловыми параметрами:
– теплоемкостью Сr;
– теплоотдачей Вr;
– потерями мощности DРr.
Допустим, что в течение времени dt в обмотке выделится количество тепла DРr×dt. Часть этого тепла вызывает превышение температуры обмотки на dt, остальная выделяется в окружающую среду. С учетом этого уравнение теплового баланса имеет вид:
DРr×dt = Сr×dt + Вr×t×dt.
Подставив в это уравнение выражение для потерь в обмотке, полученное ранее, получим:
I2×r0×dt + I2×r0×a0×t×dt +kc×DРc×dt = Сr×dt + Вr×t×dt.
Преобразуем выражение:
(I2×r0 + kc×DРc)×dt = Сr×dt + (Вr – I2×r0×a0)×t ×dt.
Введем следующие обозначения:
- эквивалентные потери мощности DРэ = I2×r0 + kc×DРc;
- эквивалентная теплоотдача Вэ = Вr – I2×r0×a0.
Выражение примет вид:
DРэ×dt = Сr×dt + Вэ×t×dt.
Разделим выражение на Вэ и обозначим отношение 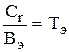 как эквивалентную постоянную времени:
как эквивалентную постоянную времени:
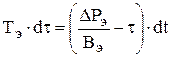 .
.
Отношение 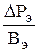 представляет собой перегрев обмотки при t ® ¥ (установившийся перегрев t¥). Выражение примет вид
представляет собой перегрев обмотки при t ® ¥ (установившийся перегрев t¥). Выражение примет вид
Тэ×dt = (t¥ – t)×dt.
Проинтегрировав это выражение, получим уравнение для перегрева обмотки:
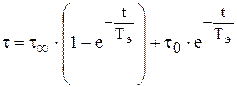 .
.
При t ® ¥ 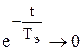 . Следовательно t ® t¥ (DРэ = Вэ×t¥) – все выделяемое в обмотке тепло рассеивается в окружающую среду. Наступает тепловое равновесие. Т.е. первое слагаемое уравнения характеризует нагрев обмотки.
. Следовательно t ® t¥ (DРэ = Вэ×t¥) – все выделяемое в обмотке тепло рассеивается в окружающую среду. Наступает тепловое равновесие. Т.е. первое слагаемое уравнения характеризует нагрев обмотки.
При выключении ТД I = 0 Þ DРэ = 0 Þ t¥ = 0 Þ Вэ = Вr Þ
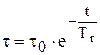 .
.
Т.е. второе слагаемое уравнения характеризует собой кривую остывания обмотки. И процесс нагрева и процесс остывания описывается экспоненциальным законом.
Из приведенных выше формул следует, что величина t¥ и Тэ зависят от величины тока, с которым работает ТД, поэтому для расчета перегрева ТД требуются две зависимости: t¥ = ¦(I) и Тэ = ¦(I).
Проанализируем, как повлияют параметры ТД на процесс нагрева. Величина теплоотдачи при неизменных потерях мощности и теплоемкости (DРэ = const; Cr = const) влияет на величину установившегося перегрева в обратной зависимости – чем больше теплоотдача, тем меньше установившийся перегрев. Увеличение теплоотдачи может быть вызвано, например, применением системы принудительной вентиляции ТЭД.
 Кроме теплоотдачи на процесс нагревания влияет теплоемкость материала обмотки и стали. При неизменных потерях и теплоотдаче (DРэ = const; Вэ = const) при увеличении теплоемкости замедляется процесс достижения установившегося перегрева, но не изменяется сама его величина – увеличивается постоянная времени, характеризующая процесс нагрева.
Кроме теплоотдачи на процесс нагревания влияет теплоемкость материала обмотки и стали. При неизменных потерях и теплоотдаче (DРэ = const; Вэ = const) при увеличении теплоемкости замедляется процесс достижения установившегося перегрева, но не изменяется сама его величина – увеличивается постоянная времени, характеризующая процесс нагрева.
Итак, мы получили аналитическое выражение для расчета перегрева обмотки ТД. К сожалению в это выражение входят величины, которые чрезвычайно сложно определить аналитически (это установившийся перегрев t¥, постоянные времени нагревания Тэ и остывания Тr). Эти величины, как правило, определяются на основании опытных данных нагревания или остывания ТД.
 Наиболее простой способ определения постоянной времени – это проведение касательной линии в начале координат к опытной линии нагревания ТД. Аналогичным образом можно поступить и с кривой остывания.
Наиболее простой способ определения постоянной времени – это проведение касательной линии в начале координат к опытной линии нагревания ТД. Аналогичным образом можно поступить и с кривой остывания.
 В том случае, когда известна только часть характеристик нагревания и остывания выбирают два равных интервала tи находят величины перегрева, соответствующие выбранным моментам времени:
В том случае, когда известна только часть характеристик нагревания и остывания выбирают два равных интервала tи находят величины перегрева, соответствующие выбранным моментам времени:

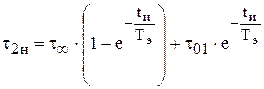 ;
;
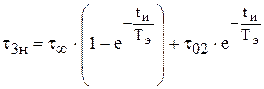 .
.
Учитывая, что t01 = t1н и t02 = t2н, можно записать:
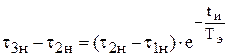 .
.
Прологарифмировав полученное выражение по основанию е, получим
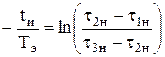 .
.
Отсюда
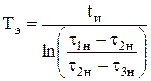 .
.
Для определения постоянной времени остывания ТД без тока достаточно одного интервала времени:
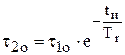 ;
;
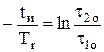 ;
;
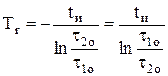 .
.
Дата добавления: 2017-03-12; просмотров: 1539;











