Материальный баланс

По веществам, участвующим в процессе, материальные балансы различают следующим образом:

- общий по всему веществу (брутто-баланс);

- частный - для одного компонента;

- элементный - для химического элемента или свободного радикала (например, баланс

- кислорода, углерода, водорода, бензольного кольца и т.д.).

Обычно в инженерных расчетах составляют балансы по первым двум вариантам. Анализ и расчет любого процесса начинают с составления материального баланса. Отметим, что материальный баланс должен включать в себя столько уравнений, сколько компонентов в перерабатываемом веществе.

По иерархической структуре производства материальные балансы подразделяют на следующие виды:

- части аппарата (т.е. части элемента процесса);

- аппарата (т.е. всего элемента процесса);

- установки (т.е. части производства);

- всего производства - от сырья до готового продукта (т.е. участка цеха, цеха или нескольких цехов);

- многих производств (т.е. комбината);

- отрасли народного хозяйства.

Обычно ограничиваются первыми тремя видами балансов, остальные изучают в специальных курсах или в инженерной практике. На основе материального баланса определяют выход продукта по сравнению с теоретически возможным (в %)‚ а также количество (массу) получаемых продуктов в единицу времени. Согласно закону сохранения, масса (количество) поступающих на переработку веществ (SG_н) должна быть равна массе веществ, получаемых в результате проведения процесса (SG_к).

SG_н = SG_к

B практических условиях при проведении технологического процесса происходят необратимые потери вещества SG_п, (например, со сточными водами или газовыми выбросами, через неплотности аппаратуры и т. п.)‚ поэтому материальный баланс в общем случае принимает вид:

SG_н = SG_к + SG_п

Для нестационарных процессов материальный баланс имеет несколько иной вид, так как потоки, направленные внутрь рассматриваемого объема (приход), и потоки, направленные наружу (расход), могут быть не равны (например, происходит накопление массы):

Приход – Расход = НакоплениеилиSG_н - SG_к = SG_{накопление}

Для стационарных процессов правая часть этого выражения равна нулю, и без учета потерь оно приобретает вид SG_н = SG_к.

Материальный и энергетический балансы в макрообъемах (например, в аппарате) при взаимодействии, например, двух фаз для тепло- или массопереноса будут зависеть от их относительного движения. Наиболее распространенные виды такого относительного движения потоков (или фаз): прямоточный или противоточный. При рассмотрении конкретных процессов тепло- и массопереноса будет показано, что температуры (для теплопереноса) или концентрации (для массопереноса) потоков на выходе из аппаратов могут существенно различаться при одних и тех же их значениях (начальных температур и концентраций) на входе.

Рассмотрим установившийся процесс поглощения газа жидкостью (абсорбцию), например поглощение аммиака водой из аммиачно-воздушной смеси при условии отсутствия перемешивания фаз по высоте аппарата. Количество компонента (аммиака), переходящего из газовой фазы в жидкую, из выражения определяется как:

М = М₁ = G(y_н – y_к) = L(х_к – х_н)

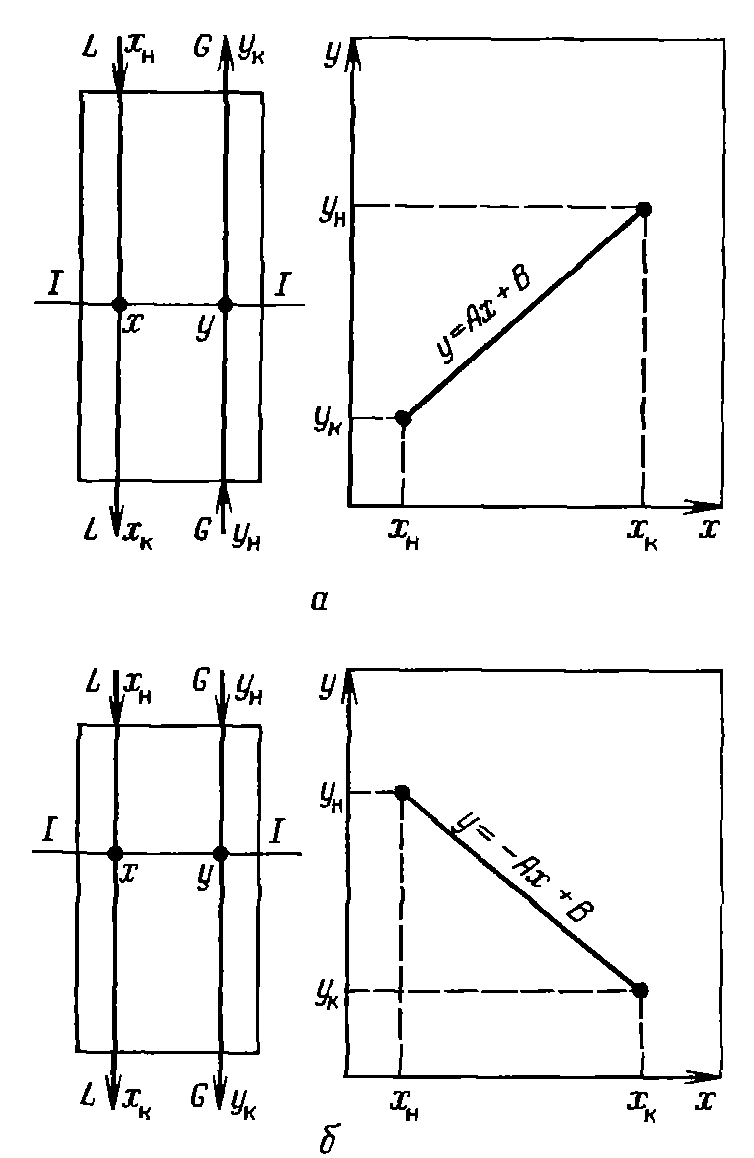
где G и L - расходы соответственно инертного газа и жидкости, кмоль/с; у_н и у_к -концентрации компонентoв газа на входе в аппарат и выходе из него, кмоль/кмоль инертного газа; х_н, х_к - концентрации компонента в жидкости на входе в аппарат и выходе из него, кмоль/кмоль инертной жидкости.

Для того чтобы получить связь между текущими концентрациями в фазах, запишем материальный баланс для верхней части аппаратов (сечение I-I):

Lx_н + Gy = Lx + Gy_к

Или

y = (L/G)x + (y_к – (L/G)x_н)

Поскольку L/G = const, a второй член правой части уравнения также является постоянной величиной, получим

у = Ах + В

где A = L/G- тангенс угла наклона прямой линии; В - отрезок, отсекаемый на оси ординат прямой линией. Это уравнение описывает связь рабочих концентраций компонента в потоках, обычно его называют уравнением рабочей линии.

Для прямоточного движения потоков уравнение рабочей линии получают по аналогии с предыдущим случаем:

у = -Ах + В

Уравнение отличается от предыдущего знаком перед коэффициентом А. Линии рабочих концентраций по этим уравнениям в дальнейшем, после рассмотрения условий равновесия систем, позволят подойти к определению движущих сил процессов переноса массы.