Плотность потока поглощенного излучения

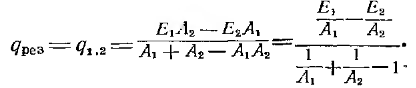
Метод эффективных потоков излучения.

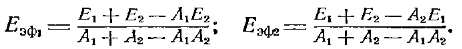
Метод сальдо. В этом случае для определения q_1,2эффективное излучение каждого из рассматриваемых тел в соответствии с (16.24) представляется соотношениями

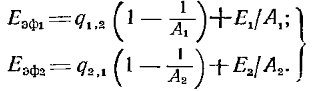
При стационарном тепловом режиме q_1,2= — q_2,1.Подставляя (17.6) в (17.4), получаем зависимость, тождественную (17.3), но более коротким путем, чем по методу многократных отражений. Теперь найдем окончательное расчетное выражение для q_1,2. Для этого в (17.3) подставим вместо плотностей потоков собственного излучения их выражении по закону Стефана — Больцмана через заданные температуры: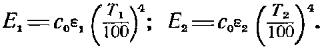

Тогда получим: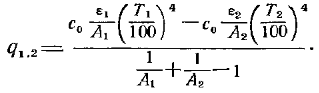

Если положить в соответствии с (16.51) e = A,то формула (17.8) упрощается;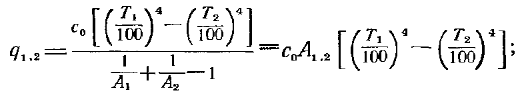

здесь А_1,2 представляет собой приведенную поглощательную способность.

Для рассматриваемой геометрической системы тел она выражается зависимостью

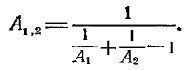
Величина

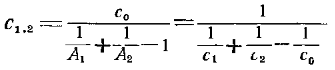
носит название приведенного коэффициента излучения и измеряется в Вт/(м²×К⁴). Приведенный коэффициент излуче-ния характеризует интенсивность результирующего излуче-ния для рассматриваемой системы двух или произвольного числа тел. Количественно он равен потоку результирую-щего излучения, отнесенному к единице поверхности рассматриваемого тела, к единице времени и к единице перепада температур в четвертых степенях между этим телом и окружающими его телами.

Величина полученного коэффициента излучения зависит от оптико-геометрических свойств данной излучающей системы тел. При c₂ = с₀ с_1,2 = с₁; при с₁ = с₂= с₀ с_1,2 = с₀. Полный результирующий поток выразится зависимостью

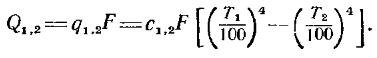
Зависимости (17.9) и (17.12) показывают, что результирующий поток прямо пропорционален приведенному коэффициенту излучения, поверхности тела и разности температур в четвертых степенях. В процессах же теплопроводности и конвекции тепловой поток пропорционален разности температур в первых степенях.