Идентификационное представление системы

Так как в большинстве случаем размерность выхода системы 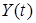намного меньше размерности вектора состояния 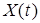динамической системы, то есть 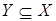, то на основе информационного множества 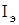нельзя идентифицировать параметры системы. Для использования множества 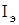в системах идентификации уравнение необходимо привести к специальному виду, который получил название наблюдателя.

Рассмотрим динамическую систему

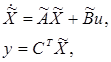(1)

где 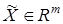— вектор состояния, 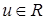, 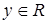— вход и выход системы, , ,

,

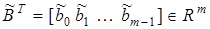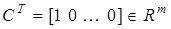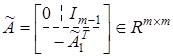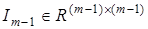— единичная матрица, 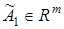— вектор параметров.

Для системы (7.1) известна информация

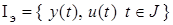. (2)

Предполагается, что система (1) является полностью наблюдаемой и управляемой.

Для идентификации системы (1) на множестве 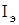ее уравнение следует привести к канонической идентификационной форме. Так как матрица С является вектором, то состояние системы (1) не может быть однозначно определено на множестве 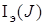, поскольку существует множество систем, имеющих идентичные выходы 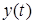при входном воздействие 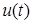. Все системы этого класса получаются с помощью преобразования

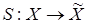
с матрицей 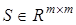, удовлетворяющей уравнению

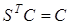, (3)

а система (1) приводится к виду

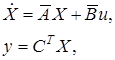(4)

где , .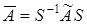

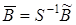Для восстановления компонент вектора X, элементов матриц 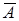, 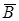применим модель

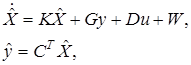(5)

где 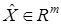, 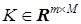— гурвицева матрица, , , , .

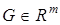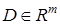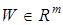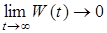Необходимость перехода от уравнения (1) к (2) связана со структурой множества 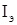. Уравнение (5) называется канонической идентификационной формой. Существует большое разнообразие канонических форм для системы (1). Наиболее общими из них являются матричные модели Ганкеля и Безу. Матрица преобразования S для этих моделей индуцируется матрицей Ганкеля и представима в виде произведения матриц достижимости и наблюдаемости. Что касается канонической формы для матриц 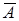и K в (4), (5), то они должны выбираться из следующих условий.

К1. Уравнение

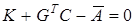
должно быть разрешимо относительно вектора G.

К2. Преобразование S должно удовлетворять как равенству (3), так и соотношению .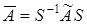

К3. Каноническая форма должна быть пригодной для синтеза адаптивных алгоритмов настройки векторов G и D.

Можно показать, что условиям К1, К2 удовлетворяет матрица 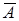, имеющая следующее каноническое представление на множестве :

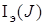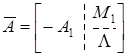, (6)

где 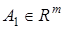— вектор параметров, 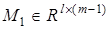, 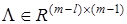— некоторые постоянные матрицы.

В адаптивных системах наиболее широкое распространение получили следующие два представления для матрицы 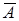, являющиеся частным случаем (6):

а) выходная каноническая форма (минимальная реализация)

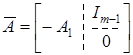; (7)

б) форма с 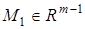и 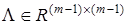вида (неминимальная реализация)

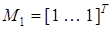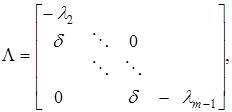, (8)

где d — символ Кронекера.

В случае б) вектор 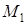и матрица L подбираются так, чтобы пара 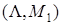была наблюдаемой.

Для восстановления вектора 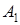и ненаблюдаемого вектора состояния 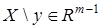в (5) по данным 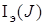применяются адаптивные наблюдатели. Каждому из приведенных выше идентификационных представлений соответствует свой АН, получаемый из (5). Так для матрицы (7) адаптивный наблюдатель явного типа имеет вид (5) с векторами

, ,

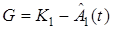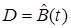где 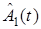, 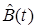— m-мерные настраиваемые векторы параметров наблюдателя, 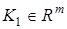— вектор параметров матрицы K.

Вектор 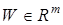(вектор обратной связи) вводится для обеспечения асимптотической устойчивости АН в случае представления (7). Для построения адаптивного наблюдателя (5) используются вспомогательные сигналы, которые получаются путем пропускания сигналов 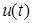, 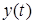через систему (филь­тры состояния)

, ,

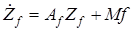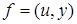где 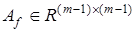— гурвицева матрица, 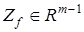— вектор вспомогательных сигналов, 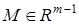— некоторый постоянный вектор.

АН явного не получил широкого распространения, что связано с необходимостью выбора вектора обратной связи. В системах управления чаще применяются адаптивные наблюдатели неявного типа. Им соответствует каноническая форма с матрицей L и вектором 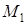типа (8). Преимущество АН неявного типа состоит в том, что для описания системы (1) порядка m можно использовать обобщенное уравнение первого порядка относительно выхода 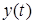. Такому описанию системы (1) соответствует модель с обобщенным входом

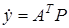, (9)

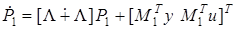, (10)

где 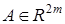— вектор параметров, 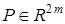— обобщенный вход, 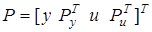, , 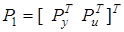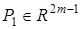— вектор вспомогательных сигналов, получаемый на основе преобразования 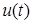и 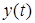, 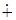— знак прямой суммы матриц.

Для восстановления вектора параметров 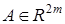и обеспечения условия

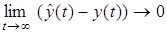
применяется адаптивный наблюдатель неявного типа

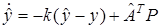, (11)

где 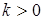— некоторое число (эталонная модель), 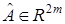— вектор настраиваемых параметров, 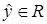выход наблюдателя.

1.3. Приведение уравнения (1) к идентификационной
форме (9), (10)

Опишем способ получения адаптивного наблюдателя Людерса-Нарен­дры (неминимальная реализация для матрицы 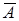). Передаточную функцию системы (1) представим в виде

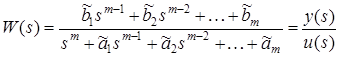. (12)

Разделим числитель и знаменатель (П7.1) на полином 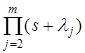, где 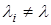, , 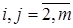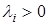. Тогда 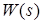можно привести к виду

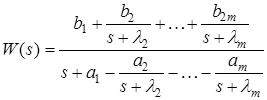. (13)

Подставляя (13) в (12) после несложных преобразований для 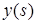получим

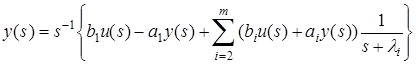. (14)

Чтобы записать это уравнение в пространстве состояний, введем обозначения

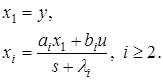(15)

Положим

, , .

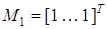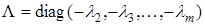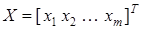Тогда идентификационное представление будет иметь вид

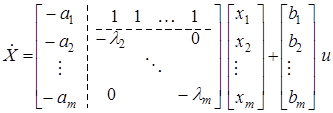. (16)

Переменные состояния системы (16) вычисляются в соответствии с (15). От уравнения (15) нетрудно перейти к модели с обобщенным входом (9), (10). Для этого достаточно положить

, , ,

.

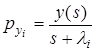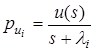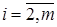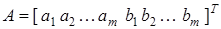В данном случае переменные состояния системы будут определяться путем решения алгебраических уравнений

.

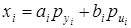
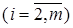Описанный подход, основанный на применении операционного метода, можно применить и для получения идентификационного представления для нестационарных систем. Но при этом необходимо учитывать, что

,

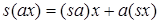где .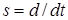

Перейдем теперь к вопросам идентификации динамических систем, приведенных к идентификационной форме (9), (10). Изложим сначала метод непрерывных 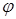-алгоритмов.

2. Метод непрерывных 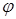-алгоритмов

Непрерывный случай

Рассмотрим задачу идентификации объекта

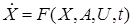, (17)

где 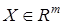— вектор состояния; 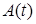— вектор параметров, принадлежащий некоторой ограниченной, но априори неизвестной области 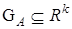; 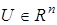— вектор управления (входа); 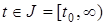; 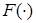— непрерывно дифференцируемая по X, A, U вектор-функция.

Под объектом будем понимать обобщенный настраиваемый объект, включающий в себя собственно объект и настраиваемую модель. На объект наложены ограничения, которые в отличие от (18) формируются на основе информации 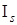, получаемой в результате анализа множества 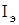при заданном уровне априорных данных ,

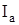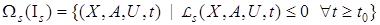, (18)

В процессе решения задачи идентификации область 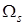может уточняться и трансформироваться, что отражено зависимостью от t в (18).

На движения системы рассматривается функционал 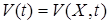(функция Ляпунова), характеризующая качество работы системы. Под целью управления понимается выполнение условия

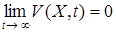. (19)

Для обеспечения (19) алгоритм принятия решений (адаптации, управления) 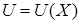должен выбираться таким, чтобы обеспечить выполнение условия

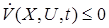. (20)

Задача сводится к выбору такого алгоритма настройки параметров обобщенного объекта

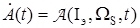, (21)

где A — искомый оператор, чтобы на движениях системы (17) при наличии ограничений (18) выполнялось целевое условие (19) или более слабое условие (20).

Рассмотрим сначала случай координатных ограничений. Найдем производную по времени от 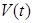с учетом (17)

.

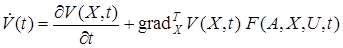При отсутствии ограничений из условия (20) алгоритм скоростного градиента

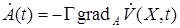, (22)

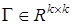( — симметрическая положительно определенная матрица), учет области 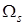приводит к более сложному алгоритму идентификации. Чтобы найти его, поступим следующим образом.

1. Осуществим расщепление функции 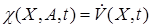на два вектора, один из которых не зависит, а второй зависит от 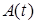. Для объектов, линейных по A, первый сомножитель будет иметь вид

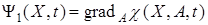
(таким путем ищется алгоритм скоростного градиента (22)). В случае нелинейной зависимости 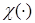от А такое расщепление осуществляется исходя из вида функции 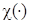и полученная составляющая обозначается через 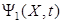. Итак, имеем

,

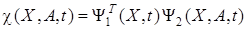где 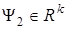— некоторая вектор-функция.

2. Следующий этап состоит в учете ограничений. Для этого осуществляется преобразование вектора 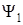в Y и функция 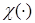приводится к так называемому F-представлению

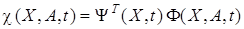, (23)

где 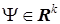— некоторая положительная вектор-функция (то есть вектор, у которого 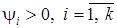), 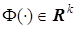— непрерывно дифференцируемая по А вектор-функция.

Вектор 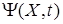в обобщенном виде отражает ограничения, накладываемые на объект. Он конструируется исходя из вектор-функции 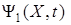с учетом области 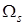(18), то есть

.

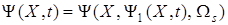Таким образом, учет ограничений 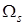приводит к такому преобразованию вектор-функции 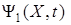, чтобы вектор-функция 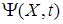была положительной

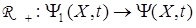
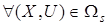. (24)

Обеспечение положительности вектора 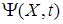объясняется применением метода функций Ляпунова и условиями реализации множества 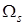. Если область 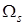является открытой, то есть на объект не наложено ограничений, то преобразование 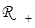является таким, что

,

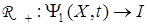где 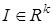— единичный вектор.

В результате применения преобразования (24) к 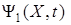вектор-функ­ция 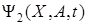также приводится к некоторой вектор-функции 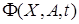, вид которой полностью определяется множеством ,

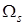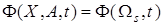. (25)

Так как 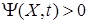, то для обеспечения условия 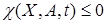, соответствующего достижению целевого условия (19), достаточно применить следующий алгоритм идентификации

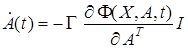, (26)

где 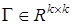— положительно определенная симметрическая матрица.

Назовем (26) адаптивным j-алгоритмом. Как следует из (25), свойства адаптивного j-алгоритма полностью определяются ограничениями, накладываемыми на объект. Что качается ограничений на помеху 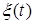, то они отражаются с помощью условия .

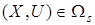Если на функцию 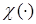наложить функциональное ограничение

,

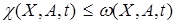где 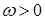— квадратичная форма от 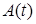, зависящая от 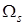, то по аналогии с (26) получим адаптивный алгоритм вида

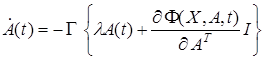, (27)

где .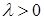

Назовем уравнение (27) пропорционально-интегральным j-алгоритмом.

Полученные законы описывают широкий класс алгоритмов идентификации. Если функция 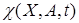является линейной по вектору настраиваемых параметров 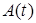, то для большинства практических случаев 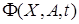будет зависеть от псевдоградиента функции 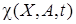. При этом функция 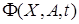должна принадлежать классу H .

Определение 5.1. Будем говорить, что вектор-функция 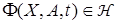, если:

1) она является непрерывно дифференцируемой по вектору А

,

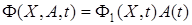где 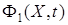— матрица Якоби;

2) матрица 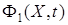является такой, что вектор 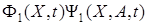является неотрицательным

.

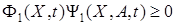
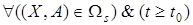Последнее условие обобщает условие псевдоградиентности на векторный случай.

Итак, если функция 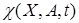является линейной по A, то из (26) и (27) можно получить класс непрерывных псевдоградиентных алгоритмов идентификации. Для данного класса алгоритмов условие устойчивости записывается в виде

.

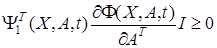Другим частным случаем, следующим из (26) и (27), является класс алгоритмов скоростного градиента

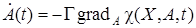, (28)

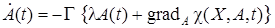. (29)

Уравнение (29) представляет собой регуляризованный вариант алгоритма (28).

Изложенная методология синтеза применима как в случае ограничений, накладываемых на вход, выход (действующую помеху), так и вектор параметров объекта

,

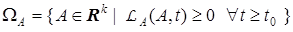где 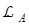— нелинейный оператор.

В задачах идентификации в качестве 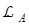чаще всего используется норма вектора А в пространстве 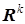. Как и в случае (18), учет ограничений 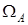приводит к F-представлению (23), но в отличие от изложенного выше вектор-функция Y будет зависеть от вектора 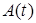. Несмотря на это к 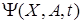предъявляются те же требования, что и при учете области .

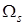Учет множества 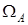имеет свою специфику, которая, естественно, отразится на классе получаемых алгоритмов. При 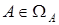адаптивный алгоритм записывается в виде

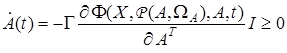. (30)

Матрица 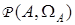играет роль индикатора принадлежности и имеет вид

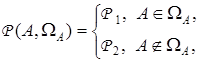
где 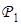, 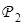— некоторые матрицы, конструируемые на основе множества 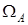. В частности, 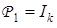, , 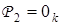где 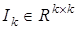, 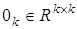— соответственно единичная и нулевая матрицы. В общем случае 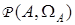является функцией k-значной логики.

В отличие от закона (26) нелинейность алгоритма (30) проявляется в зависимости вектора 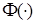от матрицы .

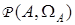Заметим, что в качестве 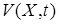при синтезе j-алгоритмов могут использоваться как локальные, так и интегральные функционалы. В локальном случае для функционала 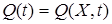имеем 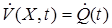, а в случае интегрального функционала 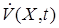равно подынтегральной функции.