Синтез адаптивных наблюдателей

Для построения адаптивных наблюдателей динамических систем, в основном, применяются два подхода. Первый их них основан на теории гиперустойчивости, а второй — на прямом методе Ляпунова. Наиболее широко в системах управления применяется второй подход. Сейчас также при синтезе адаптивных систем используется принцип пассивности, который является аналогом второго метода Ляпунова. Для АН он является неактуальным. Адаптивные наблюдатели неявного типа обладают низкой скоростью сходимости, так как их свойства зависят от частотных свойств входа 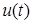. В реально работающих системах условие частотного богатства часто не выполняется и поэтому для повышения эффективности функционирования АН должны разрабатываться соответствующие подходы и методы. Один из таких подходов основан на применении редуцированных адаптивных наблюдателей. Второй путь связан с анализом и использованием имеющейся информации 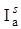о системе.

Ниже излагаются два подхода к построению адаптивных наблюдателей неявного типа. Первый базируется на получении и использовании ограничений на систему идентификации, а второй — на управлении параметрами алгоритма адаптации.

Рассмотрим объект (9), (10) и адаптивный наблюдатель (11). Вектор параметров модели (АН) (11) представим в виде

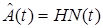, (31)

где 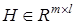— некоторая постоянная матрица, 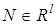— вектор мультипликативных настраиваемых параметров.

При соответствующем выборе матрицы H для вектора 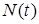можно обеспечить выполнение условия

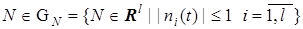(32)

Параметрический синтез АН с редуцированным числом настраиваемых параметров (АНР) сводится к выбору матрицы H и определению закона настройки вектора 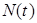. Для выбора матрицы H положим 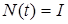, где 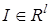— единичный вектор, и обозначим 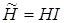. Тогда

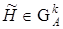. (33)

Из (33) для матрицы H получаем

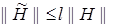. (34)

Процедура определения матрицы H сводится к следующему. Решение уравнения (11) при 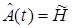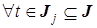имеет вид

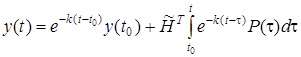. (35)

Введем переменные

,

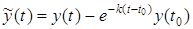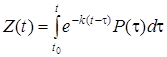
и (35) запишем в виде

.

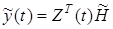Из этого уравнения для 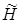получим

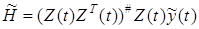, (36)

где 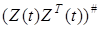— псевдообратная матрица.

После определения матрицы H переходим к синтезу алгоритма настройки вектора 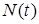. Уравнение для ошибки идентификации имеет вид

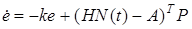, (37)

где 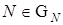при .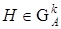

На движениях системы (37) рассмотрим функцию Ляпунов 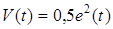. Производная 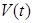приводится к F –представлению

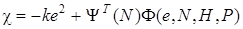, (38)

где 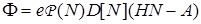, 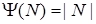— абсолютная величина от вектора 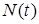, 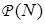— индикатор принадлежности вектора N области .

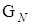Из (38) получаем j-алгоритм адаптации вектора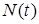

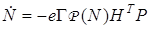, (39)

где 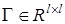— симметрическая положительно определенная матрица. Если индикатор 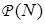задать в виде

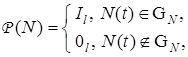
то мультипликативный j-алгоритм для 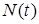примет вид

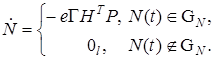(40)

Схема адаптивного наблюдателя с вектором мультипликативных настраиваемых параметров 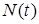показана на рис. 1.

Если матрица 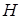является единичной, то 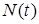совпадает с 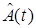в (11) и, следовательно, алгоритм (39) является законом адаптации АН (11).

Если не учитываются ограничения, то алгоритм (40) примет вид

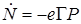. (41)

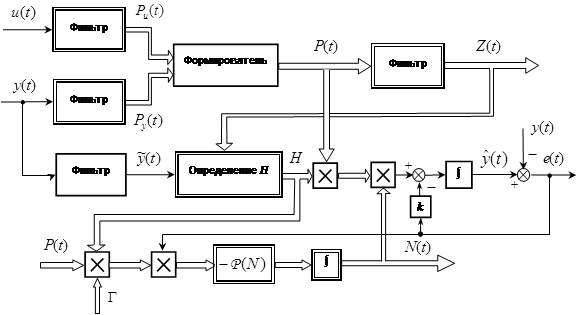
Рис. 3. Структурная схема адаптивного наблюдателя с редуцированным числом настраиваемых параметров

Схема полученной адаптивной системы показана на рис. 3.

Если вектор 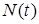совпадает с 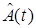в (11), то при невыполнении условия частотного богатства получить состоятельные оценки вектора 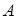не удастся. В этом случае для обеспечения сходимости алгоритма (41) следует искать закон управления матрицей G. Это сложная проблема, требующая привлечения теории обратной связи. Приведем выражение для матрица G. Для этого введем задатчик 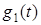, который задает эталонное изменение ошибки 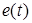. Для выбора 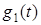зададим функциональное ограничение на процессы, протекающие в адаптивной системе,

,

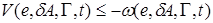где 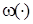— положительно определенная квадратичная форма

,

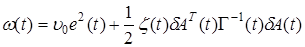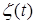— положительная ограниченная функция: 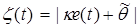, 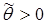— некоторое число, , , .

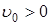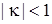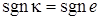Представим матрицу G в ви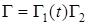де , где 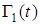— ограниченная матрица с 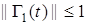, 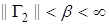. Тогда закон управления матрицей 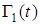имеет вид

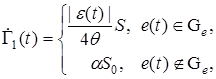(42)

где 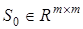— диагональная положительно определенная матрица, 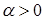— сколь угодно малое число, , .

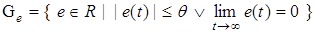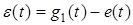Если матрица 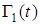удовлетворяет (42), то адаптивная система идентификации будет асимптотически устойчивой, а значит 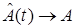при .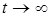

Схема системы идентификации показана на рис. 4.

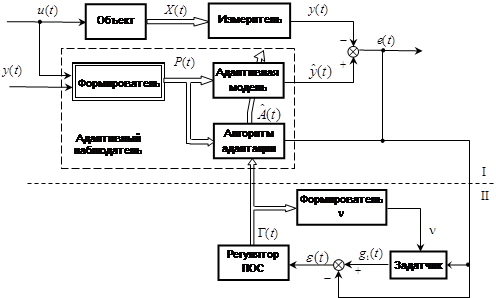
Рис. 4. Адаптивный наблюдатель с переменным коэффициентом усиления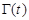

Заметим, что решение задачи идентификации непрерывных динамических систем намного сложнее, чем задачи оценивания параметров статической системы. Это связано с решением нелинейных и нестационарных систем дифференциальных уравнений.