Типы ограничений в системах идентификации

В теории управления можно выделить следующие виды ограничений:

1. Ограничения, накладываемые на состояние объекта.

2. Ограничения на управляющие переменные.

3. Ограничения на параметры объекта или управляющего устройства.

4. Функциональные ограничения.

5. Ограничения на действующие возмущения.

Как правило, ограничения 1–3, 5 формируются априори и могут быть представлены в виде интервала значений. Более сложным является процесс формирования функциональных ограничений. В общем случае они записываются в виде

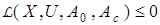, (29)

где L — некоторый оператор, 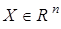, 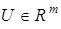— соответственно векторы состояния и управления, 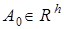, 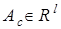— соответственно векторы параметров объекта и управляющего устройства.

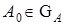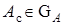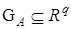Чаще всего L является интегральным или нелинейным оператором. Предполагается, что векторы , , где — область параметрических ограничений.

Функциональные ограничения являются наиболее общим видом ограничений, накладываемых на систему. Как правило, они зависят от параметров и переменных состояния объекта, а так же функционала, определяющего качество работы системы. Чаще всего функциональные ограничения получаются в результате решения задачи оптимизации и задают класс допустимых алгоритмов управления. Учитывая сказанное выше, неравенство (29) можно записать следующим образом

,

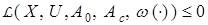где функционал 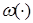отражает качество переходных процессов в системе. Если функция 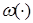не задана, то из (29) можно получить ограничения первых двух типов.

4.2. Метод адаптивных 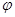-алгоритмов

Рассмотрим дискретную динамическую систему

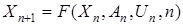, (31)

где 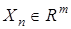— вектор состояния; 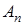— вектор параметров, принадлежащий некоторой ограниченной, но априори неизвестной области 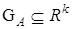; 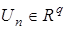— вектор управления (входа); n — дискретное время; 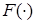— непрерывно дифференцируемая по 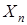, , 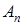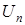вектор-функция. На систему (31) наложены ограничения типа (30).

На движениях системы (31) рассматривается функционал (функция Ляпунова) 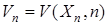. Алгоритм адаптации параметров модели 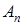ищется таким образом, чтобы выполнялось целевое условие

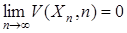, (32)

или

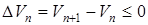. (32а)

При отсутствии алгоритм адаптации вектора 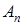имеет вид

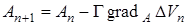. (33)

Закон (33) можно рассматривать как дискретный аналог алгоритма скоростного градиента.

Изложим метод получения дискретных j-алгоритмов идентификации.

Перепишем неравенство (32а) в виде

.

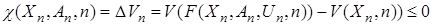Считаем, что функция 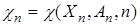является непрерывно дифференцируемой по 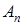почти всюду за исключением конечного числа точек. Тогда для 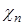, как и в непрерывном случае, справедливо следующее F-представление

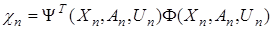, (34)

где 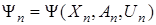, 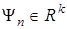— положительная вектор-функция, способ построения которой будет описан далее; 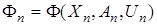, 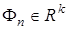— непрерывно дифференцируемая по 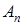вектор-функция.

Так как 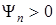, то для обеспечения условия (32а) достаточно применить следующий алгоритм параметрического оценивания

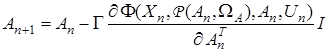, (35)

где 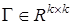— положительная симметрическая матрица, 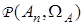— матричный индикатор принадлежности.

Если на систему (31) наложить функциональное ограничение

,

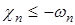где 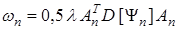, 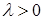— некоторое число, то получим следующую процедуру

.

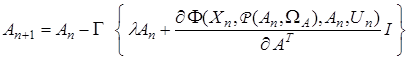Если функция 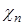является линейной по 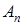, то уравнение (35) описывает класс итерационных псевдоградиентных алгоритмов. Приведем общую запись псевдоградиентного алгоритма идентификации для объекта управления с одним выходом, модель которого описывается уравнением авторегрессии – скользящего среднего:

,

,

,

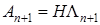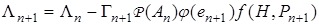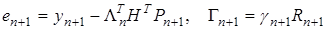где 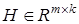— некоторая постоянная матрица, выбираемая из условия 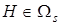; ; 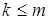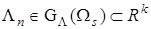— вектор настраиваемых параметров; 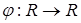— нелинейная функция; 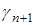— положительная последовательность чисел; 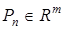— обобщенный вход; 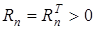— положительно определенная матрица; 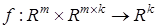— нелинейная вектор-функция; 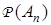— матричный индикатор принадлежности .

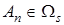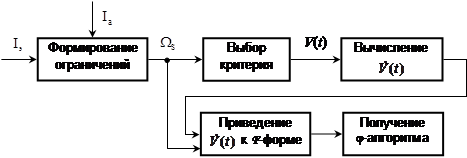
Рис. 2. Этапы синтеза j-алгоритмов

Таким образом, метод адаптивных j-алгоритмов идентификации (как непрерывных, так и дискретных) позволяет учесть реальные условия функционирования объекта и синтезировать оптимальные законы оценивания, соответствующие этим условиям. В отличие от известных подходов к выбору алгоритмов идентификации данный подход позволяет выделить лишь те переменные и связи, от которых зависит качество работы системы идентификации, а затем использовать их в алгоритмах адаптации параметров модели. Конструктивность получаемых решений является основной отличительно особенностью метода j-алгоритмов. Этапы синтеза j-алгоритмов приведены на рис. 2.

Примеры

Рассмотрим снова систему (1)

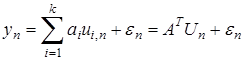. (36)

Для оценки вектора 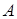применим модель

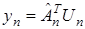. (37)

О системе (36) имеется текущая экспериментальная информация, полученная в результате измерений в процессе нормального функционирования,

,

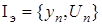где 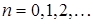— дискретное время. Имеется априорная информация о том, что 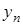содержит аномальные измерения, т. е. большие по амплитуде выбросы.

Ставится задача: необходимо на основе анализа 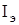разработать алгоритм оценки вектора параметров 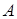системы (36) с помощью модели (37) из условия устойчивости системы идентификации.

Введем функцию Ляпунова

,

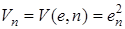где , .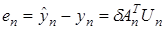

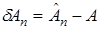Алгоритм идентификации ищем таким образом, чтобы обеспечить выполнение условия устойчивости (32а). Имеем

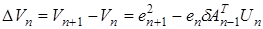. (38)

Если на систему не наложено ограничений, то получаем алгоритм (33)

.

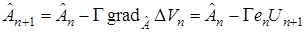Чтобы учесть ограничения, необходимо 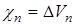привести к виду (34). Для этого следует преобразовать второе слагаемое в правой части (38). Для этого введем функцию

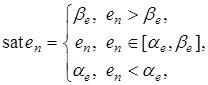(39)

где 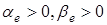— числа, задаваемые из конструктивных соображений.

Тогда, учитывая (39), для 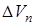получаем F-представление (34)

,

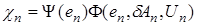где

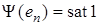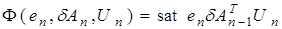, , (40)

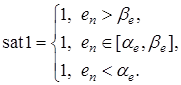
Если числа 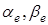могут быть отрицательными, то необходимо соответствующим образом модифицировать вид функции .

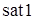Тогда 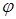-алгоритм (35) с учетом (40) примет вид

,

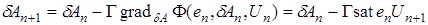откуда

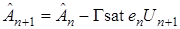. (41)

Итак, получен алгоритм идентификация системы (36)

Если вместо (39) использовать идеальную релейную функции

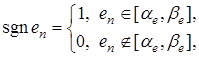
то 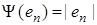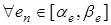, и так как 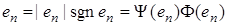, то (35) в данном случае примет вид

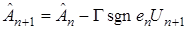. (41)

Нетрудно доказать сходимость процедур (41), (42).